- Diketahui $f$ adalah suatu fungsi sehingga $f(x) + 2f \left( \frac{1}{x} \right)= 3x$ untuk setiap $x \neq 0.$
Carilah nilai $x$ yang memenuhi $f(x) = f(−x).$ - Diketahui $ABC$ adalah segitiga lancip dengan titik – titik sudutnya terletak pada lingkaran yang berpusat di titik $O$. Titik $P$ terletak pada sisi $BC$ sehingga $AP$ adalah garis tinggi segitiga $ABC$. Jika $\angle ABC + 30◦ \le \angle ACB$, buktikan bahwa $\angle COP + \angle CAB < 90◦$.
- Tentukan semua bilangan asli $a, b$ dan $c$ yang lebih besar dari 1 dan saling berbeda, serta memenuhi sifat bahwa $abc$ membagi habis $ab + bc + ca + 2.$
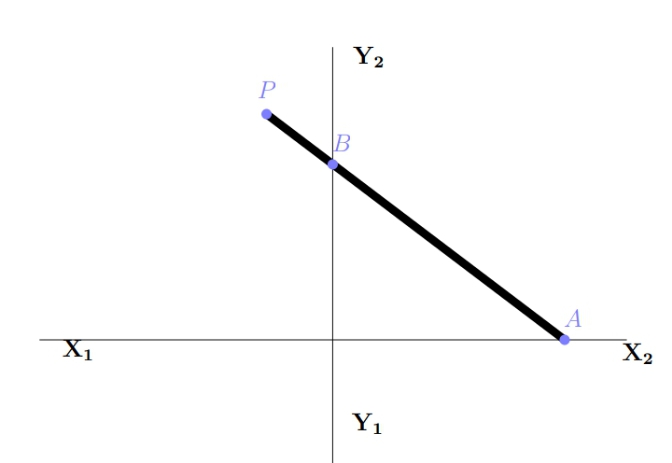
- Misalkan $A, B$ dan $P$ adalah paku – paku yang ditanam pada papan $ABP$. Panjang $AP = a$ satuan dan $BP = b$ satuan. Papan $ABP$ diletakkan pada lintasan $X_1X_2$ dan $Y_1Y_2$ sehingga $A$ hanya dapat bergerak bebas sepanjang lintasan $X_1X_2$ dan $B$ hanya bergerak bebas sepanjang lintasan $Y_1Y_2$ seperti pada gambar berikut. Misalkan $x$ adalah jarak titik $P$ terhadap lintasan $Y_1Y_2$ dan $y$ jarak titik $P$ terhadap lintasan $X_1X_2$. Tunjukkan bahwa persamaan lintasan titik $P$ adalah $\frac{x^2}{b^2}+\frac{y^2}{a^2}=1.$
- Terdapat tiga buah kotak $A, B$ dan $C$ masing – masing berisi tiga bola berwarna putih dan dua bola berwarna merah. Selanjutnya dilakukan pengambilan tiga bola dengan aturan sebagai berikut :
(a). Tahap ke-1
• Ambil satu bola dari kotak $A$.
(b). Tahap ke-2
• Jika bola yang terambil dari kotak $A$ pada Tahap ke-1 berwarna putih, maka bola tersebut dimasukkan ke kotak $B$. Selanjutnya dari kotak $B$ diambil satu bola. Jika yang terambil adalah bola berwarna putih maka bola tersebut dimasukkan ke kotak $C$. Sedangkan, jika yang terambil adalah bola berwarna merah maka bola tersebut dimasukkan ke kotak $A$.
• Jika bola yang terambil dari kotak $A$ pada Tahap ke-1 berwarna merah, maka bola tersebut dimasukkan ke kotak $C$. Selanjutnya dari kotak $C$ diambil satu bola. Jika yang terambil adalah bola berwarna putih maka bola tersebut dimasukkan ke kotak $A$. Sedangkan, jika yang terambil adalah bola berwarna merah maka bola tersebut dimasukkan ke kotak $B$.
(c). Tahap ke-3
• Ambil satu bola dari masing – masing kotak $A, B$ dan $C.$
Berapa peluang bahwa semua bola yang terambil pada Tahap ke-3 berwarna merah? - Apakah ada bilangan asli $n$ sehingga $n^2 + 5n + 1$ habis dibagi oleh 49? Jelaskan!
- Diketahui parabola $y = ax^2+bx+c$ melalui titik (−3, 4) dan (3, 16), serta tidak memotong sumbu-$X$. Carilah semua nilai absis yang mungkin untuk titik puncak parabola tersebut.
- Diketahui $T$ $ABC$ adalah limas segitiga beraturan dengan panjang rusuk 2 cm. Titik – titik $P, Q, R$ dan $S$ berturut – turut merupakan titik berat segitiga $ABC$, segitiga $T$ $AB$, segitiga $T$ $BC$ dan segitiga $T$ $CA$. Tentukan volume limas segitiga beraturan $P$ $QRS$.
Catatan : titik berat suatu segitiga adalah perpotongan ketiga garis berat. - Pada suatu acara diundang 13 tamu istimewa yang terdiri dari 8 orang pria dan 5 orang wanita. Khusus untuk semua tamu istimewa tersebut disediakan 13 tempat duduk pada satu baris khusus. Jika diharapkan tidak ada dua orang wanita yang duduk bersebelahan, tentukan banyak posisi duduk yang mungkin untuk semua tamu istimewa tersebut.
- Sebuah tabel yang berukuran n baris dan n kolom akan diisi dengan bilangan 1 atau −1 sehingga hasil kali semua bilangan yang terletak dalam setiap baris dan hasil kali semua bilangan yang terletak dalam setiap kolom adalah −1. Berapa banyak cara berbeda untuk mengisi tabel tersebut?
Keranjang Belanja
