- Robert mewarnai setiap kotak di kotak kosong berukuran 3 x 3 dengan warna merah atau hijau. Tentukan jumlah pewarnaan sehingga tidak ada baris atau kolom yang berisi lebih dari satu kotak hijau.
- Misalkan $S$ merupakan subhimpunan dari $\{1, 2, . . . , 2017\}$ sehingga untuk setiap dua elemen berbeda di $S$, baik jumlah maupun hasil kali keduanya tidak habis dibagi tujuh. Hitunglah jumlah maksimum elemen yang dapat berada di $S$.
- Annie berdiri di salah satu titik sudut segi enam beraturan. Setiap detik, ia bergerak secara independen ke salah satu dari dua titik sudut yang berdekatan dengannya, masing-masing dengan probabilitas yang sama. Tentukan probabilitas ia berada di posisi awal setelah sepuluh detik.
- Di sebuah restoran pizza, terdapat lima topping berbeda yang tersedia dan sebuah pizza dapat dipesan dengan salah satu (kemungkinan kosong) topping tersebut. Berapa banyak cara seseorang dapat memesan sepasang pizza yang tidak berurutan sehingga paling banyak satu topping muncul pada kedua pizza dan setidaknya satu topping muncul pada tidak satu pun pizza?
- Emily menggambar enam titik pada selembar kertas sedemikian rupa sehingga tidak ada tiga titik yang terletak pada satu garis lurus, lalu menggambar ruas garis yang menghubungkan setiap pasangan titik tersebut. Ia kemudian mewarnai lima ruas garis ini dengan warna merah. Pewarnaannya dikatakan bebas segitiga merah jika untuk setiap tiga titik dari enam titik yang digambarnya terdapat ruas garis tak berwarna yang menghubungkan dua dari tiga titik tersebut. Berapa banyak cara Emily dapat mewarnai gambarnya sehingga bebas segitiga merah?
- Boris memainkan permainan di mana ia melempar dua dadu empat sisi standar secara independen dan acak, dan di akhir permainan menerima sejumlah dolar yang sama dengan hasil perkalian kedua angka yang digulirkan. Namun, setelah kedua dadu digulirkan, ia dapat membayar dua dolar untuk mengulang satu dadu pilihannya, dan ia diperbolehkan membayar untuk mengulang sebanyak yang ia inginkan. Jika Boris bermain untuk memaksimalkan keuntungan yang diharapkan, berapa banyak uang, dalam dolar, yang dapat ia harapkan untuk menang dengan bermain sekali?
- Diberikan himpunan berhingga $S ⊂ \mathbb{R}^3$, definisikan $f(S)$ sebagai bilangan bulat minimum $k$ sehingga terdapat $k$ bidang yang membagi $\mathbb{R}^3$ menjadi himpunan daerah, di mana tidak ada daerah yang memuat lebih dari satu titik di $S$. Misalkan $$M(n) = maks\{f(S) : |S| = n\} \text{ dan } m(n) = min\{f(S) : |S| = n\}.$$ Evaluasi $M(200) · m(200)$.
- Andrew menghasilkan deret acak berhingga $\{a_n\}$ dari bilangan bulat berbeda berdasarkan kriteria berikut:
– $a_0 = 1, 0 < |a_n| < 7$ untuk semua $n$, dan $a_i \neq a_j$ untuk semua $i < j$.
– $a_{n+1}$ dipilih secara acak seragam dari himpunan $\{a_n − 1, a_n + 1, −a_n\}$, dengan syarat aturan di atas. Deret berakhir jika tidak ada elemen himpunan yang memenuhi syarat pertama.
Misalnya, jika $(a_0, a_1) = (1, 2)$, maka $a_2$ akan dipilih dari himpunan $\{−2, 3\}$, masing-masing dengan probabilitas $\frac{1}{2}$. Tentukan probabilitas terdapat bilangan bulat $k$ sehingga $a_k = 6$. - Dalam sebuah konferensi, enam orang memasukkan lencana nama mereka ke dalam sebuah topi, yang kemudian dikocok; satu lencana kemudian dibagikan kepada setiap orang sedemikian rupa sehingga setiap pembagian memiliki peluang yang sama. Setiap giliran, setiap orang yang belum memiliki lencana mereka sendiri mencari orang yang lencananya mereka miliki dan mengambil lencana orang tersebut. Misalnya, jika Alice memiliki lencana Bob dan Bob memiliki lencana Charlie, Alice akan memiliki lencana Charlie setelah satu giliran. Hitunglah probabilitas bahwa setiap orang pada akhirnya akan memiliki lencana mereka sendiri.
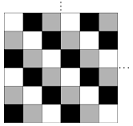
- Ryan berdiri di kotak kiri bawah dari kisi kotak berukuran 2017 x 2017, di mana setiap kotak diwarnai hitam, abu-abu, atau putih sesuai dengan pola yang digambarkan di kanan. Setiap detik ia bergerak satu kotak ke atas, satu kotak ke kanan, atau keduanya ke atas dan ke kanan, memilih di antara ketiga pilihan ini secara seragam dan independen. Dengan memperhatikan bahwa ia mulai di kotak hitam, hitunglah probabilitas Ryan masih berada di kotak hitam setelah 2017 detik.
Keranjang Belanja
