- Segitiga $ABC$ sama kaki dengan $AB = AC$. Garis bagi sudut $ABC$ dan $ACB$ berpotongan di titik $I$. Jika besar sudut $CIA$ adalah $130°$, hitunglah besar sudut $CAB$.
- Dua lingkaran memiliki jari-jari 2 dan 3, dan jarak antara pusatnya adalah 10. Misalkan $E$ adalah perpotongan dari dua garis singgung luar persekutuannya, dan $I$ adalah perpotongan dari dua garis singgung dalam persekutuannya. Hitung $EI$.
(Garis singgung luar persekutuan adalah garis singgung yang menghubungkan dua lingkaran sedemikian rupa sehingga kedua lingkaran tersebut berada pada sisi yang sama dari garis tersebut, sedangkan garis singgung dalam persekutuan adalah garis singgung yang menghubungkan dua lingkaran sedemikian rupa sehingga kedua lingkaran tersebut berada pada sisi yang berlawanan dari garis tersebut.) - Empat setengah lingkaran berjari-jari 1 ditempatkan dalam sebuah persegi, seperti yang ditunjukkan di bawah ini. Diameter setengah lingkaran ini terletak di sisi-sisi persegi dan setiap setengah lingkaran menyentuh titik sudut persegi. Tentukan selisih mutlak antara area yang diarsir dan area yang “diarsir”.
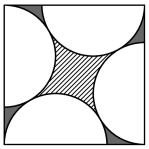
- Belah ketupat $\mathcal{R}$ memiliki diagonal pendek sepanjang 1 dan diagonal panjang sepanjang 2023. Misalkan $\mathcal{R}$’ adalah rotasi $\mathcal{R}$ sebesar $90°$ terhadap pusatnya. Jika $\mathcal{U}$ adalah himpunan semua titik yang terdapat di $\mathcal{R}$ atau $\mathcal{R}$’ (atau keduanya; ini dikenal sebagai gabungan $\mathcal{R}$ dan $\mathcal{R}$’) dan $\mathcal{I}$ adalah himpunan semua titik yang terdapat di $\mathcal{R}$ dan $\mathcal{R}$’ (ini dikenal sebagai perpotongan $\mathcal{R}$ dan $\mathcal{R}$’, hitunglah rasio luas $\mathcal{I}$ terhadap luas $\mathcal{U}$.
- Pada trapesium $ABCD, AB = 3, BC = 2, CD = 5,$ dan $∠B = ∠C = 90^o$. Garis bagi sudut $∠A$ dan $∠D$ berpotongan di titik $P$ di bagian dalam $ABCD$. Hitung $BP^2 + CP^2$.
- Misalkan $ABCD$ merupakan tetrahedron beraturan. Misalkan titik $X, Y,$ dan $Z$ masing-masing terletak pada sinar $AB, AC,$ dan $AD$ sehingga $XY = YZ = 7$ dan $XZ = 5$. Selain itu, panjang $AX, AY,$ dan $AZ$ semuanya berbeda. Tentukan volume tetrahedron $AXYZ$.
- Empat lingkaran berbeda dengan jari-jari $r$ berada pada permukaan bola satuan sehingga keduanya bersinggungan berpasangan. Tentukan $r$.
- Misalkan $ω$ adalah lingkaran satuan dengan pusat $O$ dan diameter $AB$. Sebuah titik $C$ dipilih pada $ω$. Misalkan $M, N$ adalah titik tengah busur $AC, BC,$ berturut-turut, dan misalkan $AN, BM$ berpotongan di $I$. Misalkan $AM, BC, OI$ berpotongan di suatu titik. Tentukan luas $△ABC$.
- Misalkan $△ABC$ adalah segitiga dengan pusat lingkaran $O$ yang memenuhi $AB = 13, BC = 15,$ dan $AC = 14$. Misalkan terdapat titik $P$ sehingga $PB ⊥ BC$ dan $PA ⊥ AB$. Misalkan $X$ adalah titik pada $AC$ sehingga $BX ⊥ OP$. Berapa rasio $AX/XC$?
- Titik sudut $△ABC$ diberi label berlawanan arah jarum jam, dan sisi-sisinya memiliki panjang $CA = 2022, AB = 2023,$ dan
$BC = 2024$. Putar $B$ $90^o$ berlawanan arah jarum jam terhadap $A$ untuk mendapatkan titik $B′$. Misalkan $D$ adalah proyeksi ortogonal $B′$ terhadap garis $AC$, dan misalkan $M$ adalah titik tengah ruas garis $BB′$. Kemudian, sinar $BM$ memotong lingkaran luar $△CDM$ di titik $N \neq M$. Hitung $MN$.
Keranjang Belanja
