- Misalkan $\Delta ABC$ adalah segitiga sama sisi dan $P$ adalah titik pada $\overline{BC}$. Jika $PB = 50$ dan $PC = 30$, hitunglah $PA$.
- Misalkan $ABCD$ adalah trapesium sama kaki dengan $AD = BC = 15$ sehingga jarak antara alasnya, $AB$ dan $CD$, adalah 7. Asumsikan lebih lanjut bahwa lingkaran-lingkaran dengan diameter $AD$ dan $BC$ saling bersinggungan. Berapa luas trapesium tersebut?
- Misalkan $ABC$ adalah sebuah segitiga. Garis bagi sudut $∠B$ memotong $AC$ di titik $P$, sedangkan garis bagi sudut $∠C$ memotong $AB$ di titik $Q$. Misalkan luas $\Delta ABP$ adalah 27, luas $\Delta ACQ$ adalah 32, dan luas $\Delta ABC$ adalah 72. Panjang $\overline{BC}$ dapat ditulis dalam bentuk $m\sqrt{n}$ di mana $m$ dan $n$ adalah bilangan bulat positif dengan $n$ sekecil mungkin. Berapakah $m + n$?
- Andrew si Antelop berlari pelan di sepanjang permukaan sebuah ikosahedron beraturan, yang memiliki dua puluh sisi segitiga sama sisi dan panjang rusuk 4.
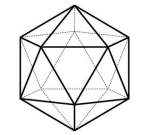
Jika ia ingin berpindah dari satu titik sudut ke titik sudut yang berlawanan, jarak minimum yang harus ia tempuh dapat dinyatakan sebagai $\sqrt{n}$ untuk bilangan bulat $n$. Hitunglah $n$. - Misalkan $P$ adalah sebuah garis sejajar dengan panjang sisi $x, y,$ dan $z$. Misalkan keempat diagonal ruang $P$ memiliki panjang 15, 17, 21, dan 23. Hitung $x^2+y^2+z^2$.$
- Pada jajargenjang $ABCD$, sudut $B$ dan $D$ lancip, sedangkan sudut $A$ dan $C$ tumpul. Garis tegak lurus dari $C$ ke $AB$ dan garis tegak lurus dari $A$ ke $BC$ berpotongan di titik $P$ di dalam jajargenjang. Jika $PB = 700$ dan $PD = 821$, berapakah $AC$?
- Misalkan $ABC$ adalah segitiga dengan pusat lingkaran dalam $I$ dan lingkaran dalam $ω$. Diketahui terdapat titik $X$ dan $Y$ pada keliling $ω$ sehingga $∠BXC = ∠BYC = 90◦$. Asumsikan lebih lanjut bahwa $X, I,$ dan $Y$ kolinear. Jika $AB = 80$ dan $AC = 97$, hitunglah panjang $BC$.
- Misalkan $ABCD$ adalah segiempat cembung yang memenuhi $AB = BC, AC = BD, ∠ABD = 80◦$, dan $∠CBD = 20◦$. Berapa derajat $∠BCD$?
- Misalkan $\Delta ABC$ adalah segitiga dengan $AB = 65, BC = 70,$ dan $CA = 75$. Sebuah setengah lingkaran $Γ$ dengan diameter $\overline{BC}$ dibangun di luar segitiga. Misalkan terdapat lingkaran $ω$ yang bersinggungan dengan $AB$ dan $AC$ dan selanjutnya bersinggungan secara internal dengan $Γ$ di titik $X$. Panjang $AX$ dapat ditulis dalam bentuk $m\sqrt{n}$ di mana $m$ dan $n$ adalah bilangan bulat positif dengan $n$ yang tidak habis dibagi kuadrat bilangan prima apa pun. Tentukan $m + n$.
- Misalkan $\Delta ABC$ adalah segitiga dengan lingkaran luar $Ω$ dan misalkan $N$ adalah titik tengah busur mayor $\widehat{BC}$. Lingkaran dalam $ω$ dari $\Delta ABC$ bersinggungan dengan $AC$ dan $AB$ masing-masing di titik $E$ dan $F$. Misalkan titik $X$ terletak pada sisi $EF$ yang sama dengan $A$ sehingga $\Delta XEF ∼ \Delta ABC$. Misalkan $NX$ berpotongan dengan $BC$ di titik $P$. Diketahui $AB = 15, BC = 16,$ dan $CA = 17$, hitung $\frac{PX}{XN}$.
Keranjang Belanja
