Tripel Pythagoras dan Persamaan Pell

- Definisi
- Contoh Soal
Definisi
Meskipun persamaan Diophantine $x^2 + y^2 = z^2$ dan $x^2 – Dy^2 = 1$ keduanya bersifat kuadrat, persamaan tersebut merupakan dasar dalam teori bilangan dan umumnya digunakan untuk menangani berbagai permasalahan dalam teori bilangan. Oleh karena itu, persamaan tersebut layak untuk dijadikan topik Bab.
Definisi 1. Tripel Pythagoras adalah himpunan tiga bilangan bulat $x, y, z$ sedemikian rupa sehingga $x^2 + y^2 = z^2;$ tripel tersebut dikatakan primitif jika FPB$(x, y, z) = 1$.
Lemma I Jika $x, y, z$ merupakan tripel Pythagoras primitif, maka $x$ dan $y$ pasti memiliki paritas yang berbeda.
Pembuktian Lemma I. Jika $x, y$ keduanya genap, maka $2$ membagi setiap $x, y, z$, sehingga FPB$(x, y, z) ≥ 2$. Jika $x, y$ keduanya ganjil, maka $z$ genap menyiratkan bahwa $z^2 \equiv 0$ (mod $4$), sedangkan $x^2 + y^2 \equiv 2$, sebuah kontradiksi.
Lemma II Jika bilangan bulat positif $a, b, c$ memenuhi $ab = c^n$ untuk beberapa $n \in \mathbb{N}$ dan $(a, b) = 1$, maka $a$ dan $b$ keduanya pangkat $n$; artinya, terdapat bilangan bulat positif $a_1, b_1$ sehingga $a = a_1^2, b = b_1^n$.
Bukti Lemma II. Kesimpulannya jelas benar jika salah satu dari $a, b$ adalah $1$. Sekarang, asumsikan bahwa $a > 1$ dan $b > 1$. Jika kita menuliskan $a, b$ dalam bentuk faktorisasi primanya, $$a=p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}\text{ dan }b=q_1^{j_1}q_2^{j_2}\cdots q_s^{j_s}$$ maka $\{p_1,p_2,…,p_r\}\cap\{q_1,q_2,…,q_s\}=\emptyset $. Tulis $c=u_1^{l_1}u_2^{l_2}\cdots u_t^{l_t}$, maka $$p_1^{k_1}p_2^{k_2}…p_r^{k_r}q_1^{j_1}q_2^{j_2}…q_s^{j_s}=u_1^{n\_1}u_2^{nl_2}…u_t^{nl_t}$$ yang menyiratkan bahwa setiap indeks di sisi kiri habis dibagi $n$. Definisikan $$a_1=p_1^{k_1/n}p_2^{k_2/n}…p_r^{k_r/n}\text{ dan }b_1=q_1^{j_1/n}q_2^{j_2/n}…q_s^{j_s/n},$$ maka $a=a_1^n,b=b_1^n$, seperti yang diinginkan.
Teorema I. Solusi bilangan bulat positif $(x, y, z)$ dari persamaan Pythagoras $$x^2+y^2=z^2\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.1)$$ memenuhi FPB$(x, y, z) = 1$ dan $2 | x$ diberikan oleh rumus $$x=2st,\text{ }\text{ }\text{ }\text{ }\text{ }y=s^2-t^2,\text{ }\text{ }\text{ }\text{ }\text{ }z=s^2+t^2,$$ di mana $s, t$ adalah dua bilangan bulat positif yang memenuhi $$s>t>0,(s,t)=1\text{ dan }s\not\equiv\text{ } (\text{mod }2).$$
Bukti. Misalkan tripel $(x, y, z)$ adalah akar primitif dari persamaan $(23.1)$ dan $x$ genap. Maka $y, z$ keduanya ganjil. Misalkan $z – y = 2u, z + y = 2v$, maka $$x^2 = (z- y)(z + y),$$ $$\left( \frac{x}{2} \right)^2 =\left( \frac{z-y}{2} \right)\left( \frac{z+y}{2} \right)=uv.$$ Karena $(u, v) = ((z-y)/2, (y+z)/2) = (z, (y+z)/2) = (z, y+z) = (z, y) = 1.$
Berdasarkan Lemma II, $u, v$ keduanya merupakan kuadrat sempurna. Misalkan $$u=t^2,\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }v=s^2$$ untuk beberapa bilangan bulat positif $s > t > 0$, maka $$z =v+u =s^2+t^2,\text{ }\text{ }\text{ }\text{ }\text{ }\text{ } y = v-u = s^2-t^2,\text{ }\text{ }\text{ }\text{ }\text{ }\text{ } x =\sqrt{4uv}=2st.$$ Misalkan $d = (s, t)$, maka $d$ membagi setiap $x, y, z$, oleh karena itu $d = 1$, yaitu $(s, t) =1$, sehingga $s, t$ tidak mungkin keduanya genap. Jika $s, t$ keduanya ganjil, maka $y$ genap, yang bertentangan dengan fakta bahwa $y$ ganjil. Jadi, $s \neq t$ (mod $2$).
Sebaliknya, misalkan $s$ dan $t$ adalah dua bilangan bulat positif yang memenuhi semua kondisi yang dijelaskan di atas, maka bilangan-bilangan yang diberikan oleh $x = 2st, y = s^2 – t^2, z = s^2 + t^2$ membentuk tripel primitif karena $$x^2+ y^2 = 4s^2t^2 +s^4-2s^2t^2 +t^4 = (s^2 + t^2)^2 = z^2,$$ dan, karena $y, z$ keduanya ganjil, $(y, z) = (s^2-t^2, s^2 + t^2) = (2s^2, s^2 +t^2) = (s^2, s^2 +t^2) = (s^2, t^2) = 1$, kita punya $(x, y, z) = 1.$
Definisi 2. Persamaan bentuk $$x^2-dy^2=1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.2)$$ disebut sebagai Persamaan Pell, di mana $d$ adalah bilangan bulat positif tetapi bukan kuadrat sempurna.
Definisi 3. Jika $(a, b)$ merupakan solusi bilangan bulat positif dari persamaan $(23.2)$ sehingga $a+\sqrt{db}$
memiliki nilai minimum, maka $(a, b)$ disebut solusi minimum atau solusi fundamental dari persamaan $(23.2)$.
Teorema II. Persamaan $(23.2)$ memiliki setidaknya satu solusi bilangan bulat positif.
Konsekuensi Persamaan Pell $(23.2)$ pasti memiliki solusi bilangan bulat positif $(x, y)$ yang tak terhingga banyaknya. Jika $(a, b)$ adalah solusi minimum dari $(23.2)$, maka semua solusi bilangan bulat positif $(x_n, y_n)$ diberikan oleh $$\left\{ \begin{array}{cl}
x_n & \frac{1}{2}[(a+\sqrt{d}b)^n+(a-\sqrt{d}b)^n], \\
y_n & \frac{1}{2\sqrt{d}}[(a+\sqrt{d}b)^n-(a-\sqrt{d}b)^n].
\end{array} \right. \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.3)$$
Teorema III. Jika $(a, b)$ merupakan solusi minimum dari $(23.2)$, maka $(x, y)$ merupakan solusi bilangan bulat positif dari $(23.2)$ jika dan hanya jika terdapat $n ∈ \mathbb{N}$ sehingga $x + \sqrt{d}y=(a+\sqrt{d}b)^n$.
Teorema IV. Ketika $d$ adalah bilangan bulat positif non-kuadrat, jika persamaan $$x^2-dy^2=-1\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.4)$$ memiliki solusi bilangan bulat positif, maka persamaan $(23.4)$ memiliki solusi bilangan bulat positif tak terhingga banyaknya. Jika $(a, b)$ adalah solusi bilangan bulat positif dengan nilai minimum $x+ \sqrt{d}y$ di antara semua solusi bilangan bulat positif $(x, y)$, maka semua solusi bilangan bulat positif $(x, y)$ dari $(23.4)$ dapat dinyatakan sebagai $$x+\sqrt{d}y=(a+\sqrt{d}b)^{2n+1},$$ dan jika $(x_o, y_o)$ adalah solusi minimum dari $(23.2)$, maka $$x_0+\sqrt{d}y_0=(a+\sqrt{d}b)^2.$$
Contoh Soal
- Buktikan bahwa persamaan $x^4+y^4 = z^2$ tidak mempunyai solusi bilangan bulat positif.
Solusi: Kita buktikan kesimpulannya dengan kontradiksi. Misalkan $(x_o, y_o, z_o)$ adalah solusi bilangan bulat positif sehingga $z_o$ adalah nilai minimum di antara semua solusi bilangan bulat positif.
Jika $(x_0,y_0)=d>1$, misalkan $p$ faktor prima $d$, maka $p^4|z_0^2$ menyiratkan bahwa $p^2|z_0$ dan $\left(\frac{x_0}{p},\frac{y_0}{p},\frac{z_0}{p^2}\right)$ juga merupakan solusi bilangan bulat positif, yang bertentangan dengan bahwa $z_o$ adalah nilai minimum di antara semua solusi bilangan bulat positif. Oleh karena itu, $(x_o, y_o) = 1.$
Karena $(x_o^2, y_o^2, z_o)$ adalah tripel Pythagoras primitif, maka terdapat $a, b ∈\mathbb{N}$ dengan $a > b, a \not\equiv b$ (mod $2$) sehingga $x_0^2 = 2ab, y_0^2 = a^2 – b^2, z_o = a^2 + b^2$.
Jika $a$ genap, maka $b$ ganjil, sehingga $y = a^2 – b^2 \equiv 3$ (mod $4$) yang mustahil, sehingga $a$ ganjil dan $b$ genap. Dari $\left(\frac{x_0}{2}\right)^2=a\left(\frac{b}{2}\right)$ dan $(a,b)=1$, ada $u,v\in\mathbb{N}$ sehingga $a=u^2,b=2v^2,(u,v)=1$. Maka $y_0^2=u^4-4v^4\Rightarrow 4v^4+y_0^2=u^4$, jadi $(2v^2,y_0,u^2)$ juga merupakan tripel Pythagoras dengan $(2v^2,u^2)=1$, oleh karena itu $(y_0,2v^2)=1$, maka $(2v^2,y_0,u^2)$ adalah tripel Pythagoras primitif. Jadi, dengan menggunakan Teorema I sekali lagi, terdapat bilangan bulat $\rho > \sigma > 0$ dengan $(\rho, \sigma) = 1$ sehingga $$2v^2=2\rho\sigma, \text{ }\text{ }\text{ }y_0=\rho^2-\sigma^2,\text{ }\text{ }\text{ }\text{ }\text{ }u^2=\rho^2+\sigma^2.$$ Karena $v^2 = \rho\sigma$, misalkan $\rho = r^2, \sigma = s^2$, maka $r,s \in \mathbb{N}, r > s > 0$ dan $(r, s) = 1.$ Jadi, $r^4 + s^4 = u^2$. Namun, $$z_o = a^2 + b^2 = u^4 + 4v^4 > u > 0.$$ yang bertentangan dengan fakta bahwa $z_o$ adalah nilai minimum.
Dengan demikian, kesimpulannya terbukti. - Buktikan bahwa persamaan $x^4 -y^4 = z^2$ tidak mempunyai solusi bilangan bulat positif.
Solusi: Misalkan $(x, y, z)$ dengan $x, y, z ∈ \mathbb{N}$ merupakan solusi persamaan $x^4 – y^4 = z^2$, dan $x$ adalah minimum di antara semua solusi tersebut. Maka $(x, y) = 1$, dan $x$ ganjil.
Jika $y$ ganjil, maka $z$ genap. Oleh karena itu, dari $(y^2)^2 + z^2 = (x^2)^2$, terdapat $a, b\in \mathbb{N}$ dengan $(a, b) = 1$ dan $a > b > 0$ sehingga $$x^2=a^2+b^2,\text{ }\text{ }\text{ }\text{ }\text{ }y^2=a^2-b^2,\text{ }\text{ }\text{ }\text{ }\text{ }z=2ab.$$ Oleh karena itu, $x^2y^2 = a^4 – b^4$. Dengan demikian, $(a, b, xy)$ juga merupakan solusi bilangan bulat positif dengan $a < x$, yang bertentangan dengan fakta bahwa $x$ minimum dalam semua solusi tersebut.
Jika $y$ genap, maka terdapat $a, b ∈ \mathbb{N}$ dengan $a > b, (a, b) = 1$ dan $a, b$ memiliki paritas yang berlawanan, sehingga $$x^2=a^2+b^2,\text{ }\text{ }\text{ }\text{ }\text{ }y^2=2ab,\text{ }\text{ }\text{ }\text{ }\text{ }z=a^2-b^2.$$ Tanpa mengabaikan keumuman, kita asumsikan bahwa $a$ genap dan $b$ ganjil. Karena $y^2 = 2ab$, terdapat $p, q∈\mathbb{N}$ dengan $(p, q) = 1$ sehingga $a = 2p^2, b = q^2$, dengan $q$ ganjil. Jadi, $x^2= 4p^4 + q^2, y = 2pq$, dan karenanya terdapat $r, s ∈ \mathbb{N}$ dengan $(r, s) = 1$ dan $r > s$ sehingga $$p^2=rs,\text{ }\text{ }\text{ }\text{ }\text{ }q^2=r^2-s^2.$$ Sekali lagi, kita dapat menuliskan $r = u^2, s = v^2$, di mana $r, s ∈ \mathbb{N}$ dengan $(u, v) = 1$. Oleh karena itu, $u^4 – v^4 = q^2$, yaitu, $(u, v, q)$ adalah solusi persamaan awal dengan $u <r < p^2 <a < x,$ sebuah kontradiksi. Dengan demikian, kesimpulannya terbukti. - Buktikan bahwa panjang jari-jari dalam segitiga Pythagoras mana pun harus bernilai bulat.
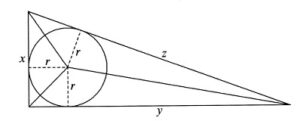
Misalkan $x, y, z ∈\mathbb{N}$ adalah panjang ketiga sisi segitiga Pythagoras dengan $x^2 + y^2 = z^2$, dan $r$ adalah panjang jari-jari dalam segitiga tersebut. Maka $$x=2kst,\text{ }\text{ }\text{ },y=k(s^2-t^2),\text{ }\text{ }\text{ }z=k(s^2+t^2)$$ untuk beberapa bilangan bulat positif $k, s, t$. Karena $\frac{1}{2}xy=\frac{1}{2} r (x + y + z),$ $$r=\frac{xy}{x+y+z}=\frac{2k^2st(s^2-t^2)}{k(2st+s^2-t^2+s^2+t^2)}=\frac{kt(s^2-t^2)}{s+t},$$ $$=kt(s-t)$$ yang merupakan bilangan bulat. - Buktikan bahwa untuk setiap bilangan asli $n$, terdapat $n$ segitiga siku-siku dengan sisi-sisi bilangan bulat, sehingga memiliki keliling yang sama dan dua buah segitiga mana pun tidak kongruen.
Solusi: Berdasarkan Teorema I, untuk setiap $n \in\mathbb{N}$, dimungkinkan untuk mendapatkan $n$ Pythagoras primitif sehingga dua segitiga siku-siku yang bersesuaian tidak kongruen. Tulis triple Pythagoras ini dengan $\{(a_k, b_k, c_k)$ dengan $0 < a_k < b_k < c_k$ untuk $k=1, 2,… , n$. Misalkan $s_k = a_k + b_k + c_k, s = s_1s_2\cdots s_n$, dan ambil $$x_k=\frac{a_ks}{s_k},\text{ }\text{ }\text{ }y_k=\frac{b_ks}{s_k},\text{ }\text{ }\text{ }z_k=\frac{c_ks}{s_k},\text{ }\text{ }\text{ }k=1,2,…,n,$$ maka masing-masing $(x_k, y_k, z_k)$ merupakan tripel Pythagoras dengan $x_k + y_k + z_k = s$. Karena dua tripel $(x_k, y_k, z_k)$ dan $(a_k, b_k, c_k)$ membentuk dua segitiga sebangun, maka kedua segitiga yang dibentuk oleh $(x_k, y_k, z_k)$ dan $(x_m, y_m, z_m)$ tidak mungkin sebangun jika $k ≠ m.$ - Temukan semua solusi bilangan bulat positif dari persamaan $x^2 – 7y^2 = 1$.
Solusi: Pertama-tama, kita cari solusi minimum $(a, b)$. Karena $x > y, (a, b)$ dapat ditemukan dengan menyatakan $y = 1, 2, …$ dan memeriksa nilai $x$ yang sesuai.
Ketika $y = 1$, tidak ada solusi untuk $x$; ketika $y = 2$, tidak ada solusi untuk $x$; ketika $y = 3$, kita peroleh $1 + 7(3^2) = 64 = 8^2$, oleh karena itu $x = 8$, yaitu $a = 8, b = 3$. Berdasarkan Konsekuensi Teorema II, solusi bilangan bulat positif $\{(x_n, y_n)\}$ diberikan oleh $$x_n=\frac{1}{2}[(8+3\sqrt{7})^n+(8-3\sqrt{7})^n],$$ $$y_n=\frac{1}{2\sqrt{7}}[(8+3\sqrt{7})^n-(8-3\sqrt{7})^n]$$ untuk $n=1,2,…,$ - $k ≥ 2$ adalah bilangan asli. Buktikan bahwa terdapat bilangan bulat $n$ tak terhingga sehingga $kn + 1$ dan $(k + 1)n + 1$ keduanya merupakan bilangan kuadrat sempurna.
Solusi: Ketika $kn + 1$ dan $(k + 1)n + 1$ keduanya merupakan kuadrat sempurna untuk beberapa $n\in \mathbb{N}$, misalkan $$kn+1=u^2, \text{ }\text{ }\text{ }\text{ }\text{ }(k+1)n+1=v^2.$$ Dengan menghilangkan $n$ dari kedua persamaan, kita memperoleh $$(k+1)u^2-kv^2=1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.5)$$ Sebaliknya, untuk setiap pasangan $(u, v)$ dua bilangan bulat positif yang memenuhi persamaan $(23.5)$, misalkan $n = v^² – u^²$, kita peroleh bahwa $kn + 1 = u^2$ dan $(k + 1)n + 1 = v^2$ yang keduanya merupakan bilangan kuadrat sempurna. Dengan demikian, cukuplah untuk menunjukkan bahwa persamaan $(23.5)$ memiliki tak terhingga banyak solusi bilangan bulat positif $(u, v)$. Dengan substitusi $$x=(k+1)u-kv\text{ dan }y=v-u,\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.6)$$ persamaan $(23.5)$ menghasilkan $$x^2-k(k+1)y^2=1,$$ yang merupakan persamaan Pell, sehingga memiliki solusi bilangan bulat positif tak terhingga $(x, y)$. Dari $(23.6)$ kita peroleh $u = x + ky$ dan $v = x + (k + 1)y$. Dengan demikian, $(23.5)$ memiliki solusi bilangan bulat positif tak terhingga $(u, v)$. - Jika $x$ adalah bilangan bulat dengan $3 < x < 200$ sehingga $x^2 + (x + 1)^2$ merupakan bilangan kuadrat sempurna, tentukan nilai $x$.
Solusi: Misalkan $x^2 + (x + 1)^2 = v^2$, maka $(2x + 1)^2 + 1 = 2v^2$. Misalkan $u = 2x + 1,$ maka $$u^2-2v^2=-1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(23.7)$$ Jelas bahwa $(u_o, v_o) = (1, 1)$ adalah solusi dari $(23.7)$, dan $(u_o, v_o)$ adalah solusi bilangan bulat positif dengan nilai minimum $x + \sqrt{2y}$ di antara semua solusi bilangan bulat positif $(x, y)$ dari $(23.7)$. Oleh karena itu, berdasarkan Teorema IV, untuk setiap solusi $(u_n, v_n)$ dari $(23.7)$, $$u_n+\sqrt{2}v_n=(1+\sqrt{2})^{2n+1},\text{ }\text{ }\text{ }n=1,2,…$$ Maka, $$u_1+\sqrt{2}v_1=(1+\sqrt{2})^3=7+5\sqrt{2}\Rightarrow x_1 =3,$$ $$u_2+\sqrt{2}v_2=(1+\sqrt{2})^5=(7+5\sqrt{2})(3+2\sqrt{2})$$ $$=41+29\sqrt{2}\Rightarrow x_2=20,$$ $$u_3+\sqrt{2}v_3=(1+\sqrt{2})^7=(41+29\sqrt{2})(3+2\sqrt{2})$$ $$=239+169\sqrt{2}\Rightarrow x_3=119,$$ $$u_4+\sqrt{2}v_4=(1+\sqrt{2})^9=(239+169\sqrt{2})(3+2\sqrt{2})$$ $$=1393+985\sqrt{2}\Rightarrow x_4=696.$$ Kesimpulannya, solusi yang diinginkan untuk $x$ adalah $20$ dan $119.$ - Suatu bilangan bulat positif dikatakan sebagai bilangan “berpangkat ganda” jika dalam faktorisasi primanya, setiap faktor prima memiliki pangkat lebih besar dari atau sama dengan $2$. Buktikan bahwa terdapat tak terhingga banyaknya pasangan bilangan bulat positif yang berdekatan sehingga keduanya merupakan bilangan berpangkat ganda.
Solusi: Perhatikan bahwa setiap bilangan kuadrat sempurna adalah bilangan berpangkat ganda, dan bilangan dalam bentuk $8y^2 = 2^3\cdot y^2$ juga berpangkat ganda. Sekarang perhatikan persamaan Pell $$x^2-8y^2=1.$$ Karena $(3, 1)$ adalah solusi fundamentalnya, maka terdapat tak terhingga banyaknya solusi bilangan bulat $(x_n,y_n),n = 1,2,…$ Karena $x_n^2 – 8y_n^2 = 1$, setiap pasangan $(8y_n^2, x_n^2)$ merupakan pasangan yang diinginkan.
Solusi dari setiap Permasalahan diberikan pada kelas online
“Every day is a chance to improve. Take it and grow!”

