Teorema Pythagoras dan Aplikasinya

- Contoh Soal
Teorema I. (Teorema Pythagoras) Untuk segitiga siku-siku dengan dua kaki $a, b$ dan sisi miring $c$, jumlah kuadrat kaki-kakinya sama dengan kuadrat sisi miringnya, yaitu $a^2 + b^2 = c^2$.
Teorema II. (Teorema Invers) Jika panjang $a, b, c$ dari tiga sisi suatu segitiga memiliki hubungan $a^2 + b^2 = c^2$, maka segitiga tersebut pastilah segitiga siku-siku dengan dua kaki $a, b$, dan sisi miring $c$.
Ketika menyelidiki segitiga siku-siku (atau singkatnya, segitiga siku-siku), kesimpulan berikut sering digunakan:
Teorema III. Suatu segitiga adalah segitiga siku-siku, jika dan hanya jika median pada salah satu sisinya adalah setengah dari sisi tersebut.
Teorema IV. Jika sebuah segitiga siku-siku memiliki sudut dalam sebesar $30°$, maka kaki di hadapannya adalah setengah dari sisi miringnya.
Contoh Soal
- Diketahui keliling segitiga siku-siku adalah $(2 + \sqrt{6})$ cm, median pada sisi miringnya adalah $1$ cm, carilah luas segitiga tersebut.
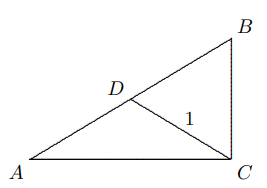
Solusi: Teorema III mengimplikasikan bahwa $AD = BD = CD = 1$, maka $AB = 2$. Misalkan $AC = b, BC = a$, maka $$a^2+b^2=2^2=4\text{ dan }a+b=\sqrt{6}$$ Oleh karena itu $6=(a+b)^2=a^2+b^2+2ab$, maka $$ab=\frac{6-4}{2}=1,$$ luas segitiga $ABC$ adalah $\frac{1}{2}$. - Seperti yang ditunjukkan pada gambar, $∠C = 90◦, ∠1 = ∠2, CD = 1,5$ cm, $BD = 2,5$ cm. Tentukan $AC$.
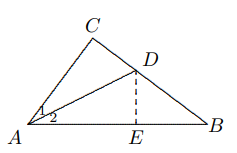
Solusi: Dari $D$, masukkan $DE ⊥ AB$, yang berpotongan dengan $AB$ di $E$. Ketika kita melipat bidang tempat $\Delta CAD$ berada di sepanjang garis $AD$, maka $C$ berimpit dengan $E$, sehingga $$AC=AE,\text{ }DE=CD=1.5\text{ (cm)}.$$ Dengan menerapkan Teorema Pythagoras pada $\Delta BED$, $$BE=\sqrt{BD^2-DE^2}=\sqrt{6.25-2.25}=2\text{ (cm)}.$$ Misalkan $AC = AE = x$ cm dan menerapkan Teorema Pythagoras pada $\Delta ABC$ menghasilkan persamaan $$(x+2)^2=x^2+4^2,$$ $$4x=12,∴ x = 3.$$ Jadi, $AC=3$ cm. - Seperti yang ditunjukkan pada gambar, $ABCD$ adalah persegi, $P$ adalah titik dalam sehingga
$PA : PB : PC = 1 : 2 : 3$. Tentukan $∠APB$ dalam derajat.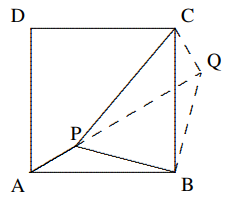
Solusi: Tanpa mengabaikan keumumannya, kita asumsikan bahwa $PA = 1, PB = 2, PC =3$. Putar $\Delta APB$ mengelilingi $B$ sebesar $90◦$ searah jarum jam, sehingga $P → Q, A → C$, maka $\Delta BPQ$ adalah segitiga siku-siku sama kaki, oleh karena itu $$PQ^2=2PB^2=8,CQ^2=PA^2=1,$$ Oleh karena itu, berdasarkan Teorema Pythagoras, $$PC^2=9=CQ^2+PQ^2,\text{ }\angle CQP=90^o.$$ Maka $\angle APB=\angle CQB=90^o+45^o=135^o.$ - Diagram menunjukkan segi enam $ABCDEF$ yang terdiri dari lima segitiga siku-siku sama kaki $ABO, BCO, CDO, DEO, EFO$, dan segitiga $AOF$, dengan $O$ adalah titik potong garis $BF$ dan $AE$. Diberikan $OA = 8$ cm, tentukan luas $\Delta AOF$ dalam cm².
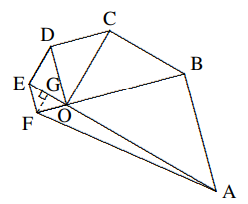
Solusi: Bentuk $$OC=\frac{1}{\sqrt{2}}OB=\left(\frac{1}{\sqrt{2}}\right)^2OA=\frac{1}{2}OA,$$ $$OE=\frac{1}{\sqrt{2}}OC=\frac{1}{4}OA=2\text{ (cm)}.$$ Karena Rt$\Delta EFO\sim$ Rt$\Delta ABO,$ $$EF=OF=\frac{1}{4}OB=\frac{1}{4\sqrt{2}}OA.$$ Misalkan $FG\bot AE$ di $G$, maka $FG=\frac{1}{\sqrt{2}}OF$
$=\frac{1}{8}OA=1$ cm. Maka, Luas $\Delta AOF$, $S_{\Delta AOF}$, diberikan oleh $$S_{\Delta AOF}=\frac{1}{2}AO\cdot FG=4\text{ }(\text{cm}^2).$$ - (Rumus median) Pada $\Delta ABC$, $AM$ adalah median pada sisi $BC$. Buktikan bahwa $AB^2 + AC^2 = 2(AM^2 + BM^2)$.
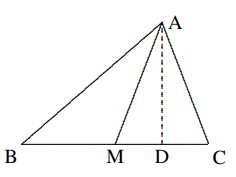
Solusi: Misalkan $AD ⊥ BC$ pada titik $D$. Berdasarkan Teorema Pythagoras, $$AB^2=BD^2+AD^2=(BM+MD)^2+AD^2$$ $$=BM^2+2BM\cdot MD+MD^2+AM^2-MD^2$$ $$=BM^2+AM^2+2BM\cdot MD.$$ Demikian pula, kita punya $$AC^2=CM^2+AM^2-2MC\cdot MD.$$ Dengan demikian, dengan menambahkan kedua persamaan tersebut, karena $BM = CM$, $$AB^2+AC^2=2(AM^2+BM^2).$$ Catatan: Jika $AM$ diperluas ke $E$ sehingga $ABEC$ merupakan jajargenjang, maka rumus mediannya sama dengan aturan jajargenjang: $$AB^2+BE^2+EC^2+CA^2=AE^2+BC^2.$$ - Pada gambar, $∠C = 90◦, ∠A = 30◦, D$ adalah titik tengah $AB$ dan $DE ⊥ AB, AE = 4$ cm. Tentukan $BC$.
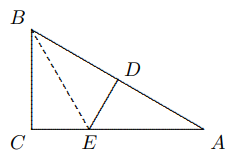
Solusi: Hubungkan $BE$. Karena $ED$ adalah garis bagi tegak lurus $AB, BE = AE$, maka $∠EBD = ∠EBA = ∠A = 30◦, ∠CBE = 60◦ − 30◦ = 30◦,∴ CE = 12BE = DE = 12AE = 2$ cm.
Sekarang misalkan $BC=x$ cm, maka dari Teorema Pythagoras, $$(2x)^2=x^2+6^2\Longrightarrow x^2=12\Longrightarrow x=\sqrt{12}=2\sqrt{3}\text{ cm}.$$ Maka, $BC=2\sqrt{3}$ cm. - Untuk $\Delta ABC, O$ adalah titik dalam, dan $D, E, F$ masing-masing berada pada $BC, CA, AB$, sehingga $OD ⊥ BC, OE ⊥ CA$, dan $OF ⊥ AB$. Buktikan bahwa $AF² + BD² + CE² = BF² + DC² + AE²$.
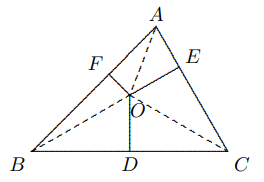
Solusi: Dengan menerapkan Teorema Pythagoras pada segitiga $OAF, OBF, OBD, OCD, OCE$ dan $OAE$, maka dapat disimpulkan bahwa
$AF^2+BD^2+CE^2$
$=AO^2-OF^2+BO^2-OD^2+CO^2-OE^2$
$=(BO^2-OF^2)+(CO^2-OD^2)+(AO^2-OE^2)$
$BF^2+DC^2+AE^2$
Kesimpulannya terbukti. - Pada diagram di bawah ini, $P$ merupakan titik interior $\Delta ABC, PP_1 ⊥ AB, PP_2 ⊥ BC, PP_3 ⊥ AC$, dan $BP_1 = BP_2, CP_2 = CP_3$, buktikan bahwa $AP_1 = AP_3$.
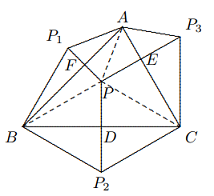
Solusi: Untuk segi empat $AP_1BP$, karena kedua diagonalnya saling tegak lurus,
$AP_1^2+BP^2=AF^2+P_1F^2+BF^2+PF^2$
$=AP^2+BP_1^2.$
Dengan mempertimbangkan $AP_3CP$ dan $PCP_2B$ masing-masing, maka dapat disimpulkan bahwa $$AP^2+CP_3^2=AP_3^2+PC^2,$$ $$BP_2^2+PC^2=PB^2+CP_2^2.$$ Kemudian menambahkan ketiga persamaan tersebut menghasilkan $$AP_1^2=AP_3^2, ∴AP_1=AP_3.$$ - Pada persegi $ABCD$, $M$ adalah titik tengah $AD$ dan $N$ adalah titik tengah $MD$. Buktikan bahwa $∠NBC = 2∠ABM$.
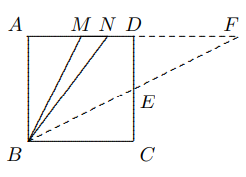
Solusi: Misalkan $AB = BC = CD = DA = a$. Misalkan $E$ adalah titik tengah $CD$. Misalkan garis $AD$ dan $BE$ berpotongan di $F$.
Berdasarkan simetri, kita peroleh $DF = CB = a$. Karena segitiga siku-siku $ABM$ dan $CBE$ simetris pada garis $BD$, maka $∠ABM = ∠CBE$. Cukuplah menunjukkan $∠NBE = ∠EBC$, dan untuk ini kita hanya perlu menunjukkan $∠NBF = ∠BFN$ karena $∠DFE = ∠EBC$.
Dengan asumsi kita punya $$AN=\frac{3}{4}a,\text{ }∴NB=\sqrt{(\frac{3}{4}a)^2+a^2}=\frac{5}{4}a.$$ Di sisi lain, $$NF=\frac{1}{4}a+a=\frac{5}{4}a,$$ Jadi $NF=BN$, maka $\angle NBF=\angle BFN$.
Solusi dari setiap Permasalahan diberikan pada kelas online
“I am not a product of my circumstances. I am a product of my decisions.”

