Sifat Dasar Lingkaran

- Contoh Soal
- Lingkaran bersifat simetris terhadap pusatnya, dan juga simetris terhadap setiap diameternya. Oleh karena itu, setiap sudut yang sama dipusatnya dibatasi oleh tali busur yang sama dan busur yang sama, begitu pula sebaliknya.
- Diameter membagi dua sebuah tali busur dan busur yang dibentuknya jika dan hanya jika diameter tersebut tegak lurus terhadap tali busur. Dengan menggunakan sifat ini, mudah untuk membuktikan bahwa dua busur di antara dua tali busur yang sejajar adalah sama.
- Sudut pada lingkaran sama dengan setengah dari sudut pusat yang dibatasi oleh tali busur atau busur yang sama. Sudut pusat dapat diukur dari busur yang dibatasinya dalam derajat. Oleh karena itu, sudut pada lingkaran dapat diukur dalam derajat dari setengah dari busur yang dibatasinya.
Secara khusus, sudut pada lingkaran yang dibatasi oleh diameter harus $90^o$. - Untuk lingkaran dengan jari-jari $R$ dan tali busur dengan panjang $21$, maka garis tegak lurus jarak pusat dari tali busur, dilambangkan dengan $d$, diberikan oleh $$d=\sqrt{R^2-l^2}.$$
Contoh Soal
- Pada gambar $P,Q$ dan $R$ adalah tiga titik pada lingkaran yang pusatnya adalah $O$. Garis $PO$ dan $QR$ diproduksi untuk bertemu di $S$. Misalkan $RS=OP$ dan $\angle PSQ=12^o$ dan $\angle POQ=x^o$. Tentukan nilai $x$.
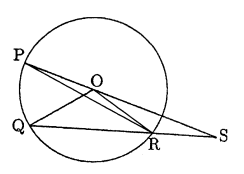
(A) 36 (B) 42 (C) 48 (D) 54 (E) 60
Solusi: Menghubungkan $PR,OR$. Maka $OR=RS$ menyiratkan bahwa $\angle SOR=\angle PSR=12^o$, maka $$\angle SPR=6^o$$ Karena $\frac{x}{2}=\angle PRQ=\angle SPR+PSR=18^o$, oleh karena itu $x=36$, jawaban nya adalah (A). - Misalkan $\Delta ABC$ adalah segitiga sama sisi yang tertulis dalam sebuah lingkaran, dan misalkan $M$ adalah sebuah titik pada busur $BC$. Buktikan bahwa $MA=MB+MC$.
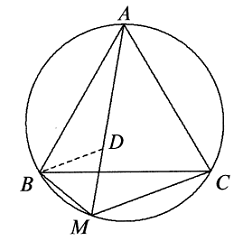
Solusi: Sudah jelas bahwa $AM>CM$. Pada $AM$ ambil titik $D$ sehingga $AD=CM$. Itu sudah cukup menunjukkan bahwa $MB=MD$. Karena $AB=BC,AD=CM$ dan $\angle BAM=\angle BCM$, $$ ∴\Delta ABD\cong \Delta CBM.$$ Maka, $BM=BD$ dan $\angle ABD=\angle CBM$. Untuk $\Delta BMD,\angle DBM=\angle ABC=60^o$, Jadi, $\Delta DBM$ adalah sama sisi, maka $MB=MD$. - Misalkan $ABCD$ merupakan segiempat yang terdapat dalam lingkaran berdiameter $AC$, dan misalkan $E$ merupakan kaki garis tegak lurus dari $D$ ke $AB$, seperti yang ditunjukkan pada gambar dibawah ini. Jika $AD=DC$ dan luas segiempat $ABCD$ adalah $24 \text{ cm}^2$, tentukan panjang $DE$ dalam cm.
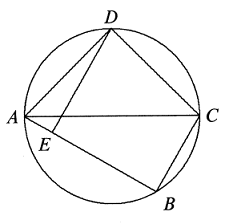
(A) $3\sqrt{2};$ (B) $2\sqrt{6};$ (C) $2\sqrt{7};$ (D) $4\sqrt{2};$ (E) $6$Solusi: Misalkan $r$ adalah jari-jari lingkaran dan $\angle CAB=\theta$. Hubungkan $DB$. Maka $$[ABCD]=[DAB]+[DCB]=\frac{1}{2}AD\cdot AB\sin \angle DAB+\frac{1}{2}CD\cdot CB\sin \angle BCD.$$ $$24=\frac{1}{2}\sqrt{2}r\cdot 2r\sin (90^o-\theta)\cdot \sin (45^o+\theta)+\frac{1}{2}\sqrt{2}r\cdot 2r\sin \theta \cdot \sin (135^o-\theta)$$ $$r^2[\cos \theta (\sin \theta +\cos \theta)+\sin \theta(\sin \theta+\cos \theta)]$$ $$r^2(\sin \theta+\cos \theta)^2=[\sqrt{2}r\cdot \sin(45^o+\theta)]^2$$ $$=DE^2$$ $ ∴DE=\sqrt{24}=2\sqrt{6}$, jawaban nya adalah (B).
- Pada lingkaran $⊙O$, jari-jari $r=5$ cm dan $CD$ adalah dua tali busur sejajar dan $AB=8$ cm, $CD=6$ cm. Tentukan panjang tali busur $AC$.
Solusi: Seperti yang ditunjukkan pada gambar (1) dan (2), terdapat empat kemungkinan kasus.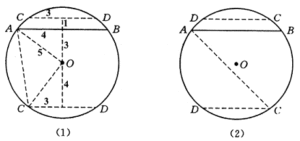
Dalam gambar (1), panjang $AC$ yang lebih panjang diberikan oleh $$AC=\sqrt{(4-3)^2+(4+3)^2}=\sqrt{50}=5\sqrt{2};$$ dan panjang $AC$ yang lebih pendek diberikan oleh $$AC=\sqrt{(4-3)^2+1^2}=\sqrt{2}.$$ Demikian pula, seperti pada gambar (2), panjang $AC$ yang lebih panjang diberikan oleh $$AC=\sqrt{(4+3)^2+(4+3)^2}=7{2};$$ dan panjang $AC$ yang lebih pendek diberikan oleh $$AC=\sqrt{(4+3)^2+1^2}=5\sqrt{2}.$$ Maka, panjang tali busur $AC$ yang mungkin $\sqrt{2},5\sqrt{2}$ atau $7\sqrt{2}$. - Segitiga $ABC$, dimana $AB<AC$, memiliki lingkaran luar $S$. Garis tegak lurus dari $A$ ke $BC$ bertemu $S$ lagi di $P$. Titik $X$ terletak pada ruas garis $AC$, dan $BX$ bertemu $S$ lagi di $Q$. Tunjukkan bahwa $BX=CX$ jika dan hanya jika $PQ$ adalah diameter $S$.
Solusi: Seperti yang ditunjukkan pada gambar,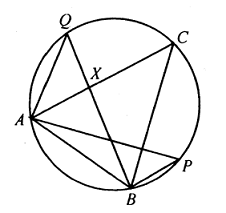
$$\angle CBP+\angle BCA=\angle CAP+\angle BCA=90^o.$$ $$\angle CBP+\angle QBC=\angle QBP.$$ $$ ∴PQ\text{ adalah diameter dari }S\Leftrightarrow \angle QBP=90^o$$ $$\Leftrightarrow \angle CBP +\angle QBC=90^o$$ $$\Leftrightarrow \angle BCA=\angle QBC$$ $$\Leftrightarrow BX=CX.$$ - Diketahui $\Delta ABC$ tertulis dalam lingkaran $⊙O$, sehingga diameter $CD$ tegak lurus terhadap $AB$ di titik $E$. Tali busur $BF$ memotong $CD$ dan $AC$ masing-masing di titik $M$ dan $N$, dan $BF=AC$. Hubungkan $AD,AM$. Buktikan bahwa
(i) $\Delta ACM\cong\Delta BCM;$
(ii) $AD\cdot BE=DE\cdot BC;$
(iii) $BM^2=MN\cdot MF.$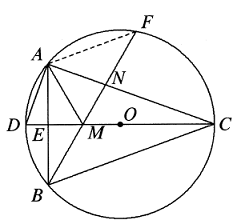
Solusi:
(i) Karena $CD$ adalah garis bagi tegak lurus dari tali busur $AB$, maka $$AM=BM,AC=BC,$$ dan $CM$ dibagikan, oleh karena itu $\Delta ACM\cong \Delta BCM$ (S.S.S.).
(ii) $AD\cdot BE=DE\cdot BC\Leftrightarrow \frac{BE}{DE}=\frac{BC}{AD}$. Dari $$\angle ADE=\angle ADC=\angle CBA=\angle CBE$$ dan $$\angle DAE=\angle DAB=\angle D=\angle BCE,$$ maka diperoleh $\Delta DAE\sim\Delta BCE$, maka $\frac{BE}{DE}=\frac{BC}{AD}$.
(iii) Hubungkan $AF\text{ }.\text{ }BF=AC\Rightarrow \widehat{BAF}=\widehat{AFC}$, maka $$\widehat{AB}=\widehat{FC}$$ yang menyiratkan bahwa $\angle CBF=\angle AFB$. Karena $\Delta ACM\cong \Delta BCM$, $$\angle AFM=\angle AFB=\angle CBF=\angle CBM=\angle CAM=\angle NAM,$$ oleh karena itu $\Delta MAN\sim\Delta MFA$, maka $\frac{MN}{MA}=\frac{MA}{MF}$, yaitu $$MA^2=MN\cdot MF,\text{ atau }BM^2=MN\cdot MF$$ karena $BM=AM$. - Lingkaran luar $⊙O$ dari segi empat $ABCD$ memiliki jari-jari $2$. $AC$ dan $BD$ berpotongan di titik $E$, sehingga $AE=EC$. Diketahui $AB=\sqrt{2}AE,BD=2\sqrt{3}$, tentukan luas dari $ABCD$.
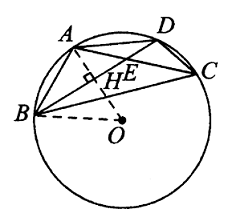
Solusi: $AE=EC$ dan $AB=\sqrt{2}AE$ memberikan $AB^2=2AE^2=AE\cdot AC$, maka $\frac{AB}{AC}=\frac{AE}{AB}$. Karena $\angle EAB=\angle BAC$, maka diperoleh $$\Delta ABE\sim\Delta ACB,$$ sehingga $$\angle ABE=\angle ACB=\angle ADB,∴AB=AD.$$ Oleh karena itu $A$ membagi dua busur $BAD$, maka $OA\bot BD$. Misalkan $H$ menjadi titik persimpangan $AO$ dan $BD$, maka $OH\bot BH$ dan $$OH=\sqrt{2^2-(\sqrt{3})^2}=1,AH=OA-OH=1\Rightarrow [ABD]=\frac{1}{2}\cdot 2\sqrt{3}\cdot 1=\sqrt{3}.$$ Karena $AE=CE\Rightarrow [BCE]=[ABE],[CDE]=[ADE]\Rightarrow [CBD]=[ABD]$, maka diperoleh $$[ABCD]=2[ABD]=2\sqrt{3}.$$ - Diketahui $P$ adalah titik tetap pada garis bagi sudut $\angle {CAB}$. Buatlah lingkaran yang melalui $A$ dan $P$. Jika lingkaran tersebut memotong sisi $AB$ dan $AC$ masing-masing di titik $M$ dan $N$, buktikan bahwa nilai $AM+AN$ tidak bergantung pada pilihan lingkaran.
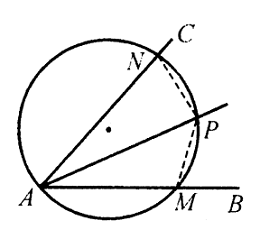
Solusi: Untuk setiap pilihan lingkaran yang melalui $A$ dan $P$, misalkan $d=AP$ dan tulis $\angle MAP=\angle NAP=\alpha$. Hubungkan $MP,NP$.
Menerapkan aturan kosinus ke $\Delta MAP$ dan $\Delta PAN$ masing-masing, karena $PM=PN$, maka diperoleh $$PM^2=d^2+AM^2-2d\cdot AM\cos \alpha,$$ $$PN^2=d^2+AN^2-2d\cdot AN\cos \alpha,$$ atau $$AM^2-2d\cos \alpha\cdot AM+(d^2-PM^2)=0$$ $$AN^2-2d\cos \alpha\cdot AN+(d^2-PM^2)=0.$$ Nilai dari $PM,PN$ diberikan jika lingkaran digambar, maka nilai yang sesuai dari $AM$ dan $AN$ adalah akar persamaan kuadrat $$x^2-2d\cos \alpha \cdot x+(d^2-PM^2)=0,$$ dan dengan teorema Vieta, $AM+AN=2d\cos \alpha$, yang tidak bergantung pada pilihan lingkaran
Solusi dari setiap Permasalahan diberikan pada kelas online
“Progress is impossible without change, and those who cannot change their minds cannot change anything.”

