Poligon Siklik

- Kriteria untuk menentukan suatu segi empat siklik
- Contoh Soal
Suatu poligon bersisi $n$ $(n \ge 4)$ dikatakan sebagai poligon siklik jika ia berada di dalam lingkaran. Dalam hal ini, $n$ titik sudutnya dikatakan konsiklik.
Bagian utama dari bab ini adalah tentang segiempat siklik, karena ini merupakan dasar untuk mempelajari poligon siklik.
Kriteria untuk menentukan suatu segi empat siklik
- Suatu segiempat $ABCD$ adalah siklik jika dan hanya jika keempat sudut dalamnya memenuhi $\angle A+\angle C=\angle B+\angle D=180^o$.
- Suatu segiempat cembung bersifat siklik jika dan hanya jika salah satu sudut luarnya sama dengan sudut dalam di hadapannya.
- Suatu segiempat cembung $ABCD$ merupakan segiempat siklik jika dan hanya jika dua sudut yang diapit oleh sisi yang sama pada $ABCD$ adalah sama besar, misalnya $\angle ACB=\angle ADB$, yang diapit oleh sisi $AB$.
- (Teorema tali busur berpotongan terbalik) Bila dua ruas garis $AC$ dan $BD$ berpotongan di titik $P$, maka segiempat $ABCD$ adalah siklik jika $AP\cdot PC=BP\cdot BD$.
- Bila dua ruas garis $AC$ dan $BD$ tidak berpotongan tetapi perpanjangannya berpotongan di titik $P$, maka segi empat $ABCD$ adalah siklik jika dan hanya jika $PA\cdot PD=PB\cdot PC$.
Bukti keniscayaan (I) hingga (III) merupakan aplikasi langsung dari sifat-sifat fundamental. Kecukupan (I) hingga (V) dapat dibuktikan dengan kontradiksi. Bukti keniscayaan (V) dapat ditemukan di bab berikutnya.
Dalam contoh-contoh di bawah ini, beberapa bertujuan untuk membuktikan bahwa titik-titik tersebut konsiklik, dan beberapa merupakan aplikasi titik-titik konsiklik untuk menyelesaikan soal-soal geometri lain yang melibatkan lingkaran.
Contoh Soal
- Pada $\Delta ABC$ $AB>AC$, garis singgung di $B$ terhadap lingkaran luar memotong garis $AC$ di $P$. $D$ adalah titik simetris $B$ terhadap $P, E$ adalah titik simetris $C$ terhadap garis $BP$. Buktikan bahwa segi empat $ABED$ merupakan siklik.
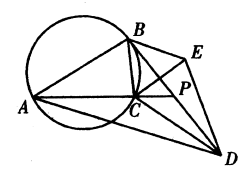
Solusi: Dengan teorema segmen alternatif, $\angle PBC=\angle BAC=\angle PAB$, oleh karena itu $\Delta PBC\sim\Delta PAB$, maka $\frac{PA}{PB}=\frac{PB}{PC}$, $$∴PA\cdot PC=PB^2=PD^2,$$ atau $$\frac{PA}{PD}=\frac{PD}{PC}$$ Karena $\angle APD$ dibagikan, $$\Delta APD\sim \Delta DPC\text{ (S.A.S.)},$$ $$∴\angle CAD=\angle PAD=\angle PDC.$$ $C$ dan $E$ simetris pada garis $BP$ menyiratkan bahwa $\angle PDC=\angle PDE=\angle BDE$ dan $\angle PBC=\angle DBE$, sehingga $$\angle BAD=\angle PAD+\angle PAB=\angle PDC+\angle PBC=\angle BDE+\angle DBE$$ $$=180^o-\angle BED.$$ Maka, segiempat $ABED$ adalah siklik. - Seperti yang ditunjukkan pada diagram di bawah ini, $ABCD$ adalah segi empat cembung, $\angle ABC=\angle ADC, E, F, G, H$ masing-masing adalah titik tengah $AC, BD, AD, CD$. Buktikan bahwa
(i) $E,F,G,H$ siklik;
(ii) $\angle AEF=\angle ACB-\angle ACD.$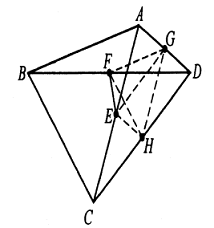
Solusi:
(i) Hubungkan $EG,EH,FG,FH,GH$ maka $FG||BA,FH||BC$, maka $$\angle GFH=\angle ABC.$$ Demikian pula, $\angle GHF=\angle ACB$. Karena $DGEH$ adalah jajargenjang, maka $$\angle GEH=\angle ADC=\angle ABC=\angle GFH,$$ oleh karena itu $EFGH$ siklik, yaitu $E,F,G,H$ adalah konsiklik.
(ii) $EFGH$ siklik $\Rightarrow \angle GEH=\angle GHF=\angle ACB$, dan $EG||CD$ menyiratkan bahwa $\angle AEG=\angle ACD$, oleh karena itu $$\angle AEF=\angle GEF-\angle AEG=\angle ACB-\angle ACD.$$ - Pada segitiga lancip $ABC$, $D$ terletak pada $AB$, lingkaran luar $\Delta BCD$ dan $\Delta ADC$ berpotongan dengan $AC$ dan $BC$ masing-masing di titik $E, F$. Misalkan pusat lingkaran luar $\Delta CEF$ adalah $O$. Buktikan bahwa pusat lingkaran luar $\Delta ADE, \Delta ADC, \Delta DBF, \Delta DBC$, dan titik $D$ dan $O$ adalah konsilikon, dan $OD\bot AB$.
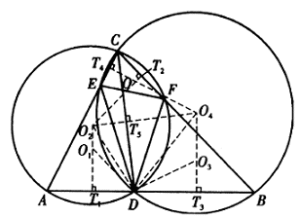
Solusi: Misalkan $O_1,O_2,O_3,O_4$ menjadi pusat lingkaran segitiga $ADE,ADC,DBF,DBC$ masing-masing. Maka $O_1O_2$ berada pada garis bagi tegak lurus $AD$ dan $O_3O_4$ berada pada garis bagi tegak lurus $DB$.
Gunakan $\alpha,\beta,\gamma$ untuk menunjukkan sudut dalam $\Delta ABC$ dan misalkan $T_1,T_2,T_3,T_4,T_5$ menjadi titik tengah segmen garis $AD,CF,BD,CE,CD$ masing-masing.
$ADFC$ bersifat siklik yang memberikan $\angle DFB=\alpha$. $O_3$ adalah pusat $\Delta DBF$ yang menyiratkan bahwa $\angle DO_3T_3=\alpha$, dan demikian pula $\angle DO_2T_5=\angle DAC=\alpha$. Di samping itu, $O_2,T_5,O_4$ kolinear, maka $\angle DO_2O_4=\angle DO_2T_5=\alpha =\angle DO_3T_3$, oleh karena itu $$O_2,O_4,O_3,D\text{ konsiklik }.\text{ }\text{ Demikian pula, }O_4,D,O_1,O_2\text{ konsiklik}.$$ Oleh karena itu $O_1$ dan $O_3$ keduanya berada di lingkaran luar $\Delta O_2O_4D$. Di samping itu, $\angle DO_2O_4=\alpha,\angle O_2O_4D=\beta$ menyiratkan bahwa $\angle O_4DO_2=\gamma$.
Di sisi lain, $CT_4OT_2$ siklik, maka $\angle T_4OT_2=180^o-\gamma$, oleh karena itu $O,O_2,D,O_4$ konsiklik. Maka, $O_1,O_2,O_3,O_4,O,D$ konsiklik.
Karena $\angle OO_4O_3=\angle T_4O_4T_3=180^o-\angle CAB=180^o-\alpha$, dan $\angle DOO_4=\angle DO_3T_3=\alpha$, maka $OD||O_3O_4$, maka $OD \bot AB$. - $ABCD$ adalah segi empat cembung, lingkaran luar $\Delta ABC$ memotong $CD, DA$ di titik $P, Q,$ dan lingkaran luar $\Delta ACD$ memotong $AB, BC$ di titik $R, S$. Garis $BP, BQ$ memotong garis $RS$ di titik $M, N$. Buktikan bahwa $M, N, Q, P$ konsiklik.
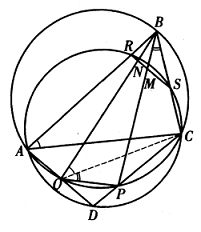
Solusi: Sudut-sudut pada lingkaran yang dibatasi oleh tali busur yang sama adalah sama besar, jadi $$\angle BQC=\angle BAC,\angle CQP=\angle CBP$$ Karena $\angle BSR=\angle RAC=\angle BAC=\angle BQC$, maka $$\angle BMN=180^o-\angle BMS$$ $$=\angle SBM+\angle BSM=\angle CBP+\angle BSR$$ $$=\angle CQP+\angle BQC=\angle BQP=\angle NQP.$$ Maka, $M,N,Q,P$ konsiklik. - Diketahui $⊙O_1$ dan $⊙O_2$ berpotongan di titik $M$ dan $N$, garis singgung persekutuan yang lebih dekat ke titik $M$ adalah garis singgung lingkaran di titik $A$ dan $B$ masing-masing. $C$ dan $D$ masing-masing adalah titik simetris $A$ dan $B$ terhadap titik $M$. Lingkaran luar $\Delta DCM$ berpotongan dengan $⊙O_1$ dan $⊙O_2$ di titik $E$ dan $F$ (yang menyimpang dari titik $M$). Buktikan bahwa jari-jari lingkaran luar $\Delta MEF$ dan $\Delta NEF$ sama.
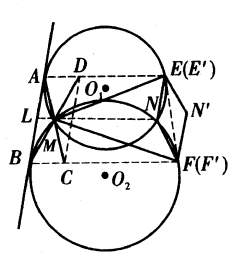
Solusi: Ambil titik $N’$ sehingga $NEN’F$ adalah jajargenjang.
Misalkan Ekstensi $AD$ dan $BC$ berpotongan dengan $⊙O_1$ dan $⊙O_2$ di $E’$ dan $F’$. Karena $M, C, F, E, D$ adalah konsiklis, $$\angle MFC=\angle MDC=\angle MBA=\angle MFB.$$ Ada $B, C, F$ yang kolinear, $F = F’$. Demikian pula, $E = E’$. Misalkan sinar $NM$ memotong $AB$ di $L$. Maka $$\Delta LAM\sim\Delta LNA\Rightarrow LA^2=LM\cdot LN$$ dan demikian pula $LB^2=LM\cdot LN$, oleh karena itu $LA=LB$.
$AC,BD$ saling membagi dua $\Rightarrow ABCD$ jajargenjang $\Rightarrow MN||BF||AE$. Oleh karena itu $O_1O_2$ tegak lurus pada $AE$ dan $BF$, dan $A,M,B$ dan $E,N,F$ simetris terhadap garis $O_1O_2$, yang menyiratkan bahwa $\angle ENF =\angle AMB$ sehingga $$\angle EN’F+\angle EMF=\angle ENF+\angle EMF=\angle AMB+\angle EMF$$ $$=\angle AMB+\angle EMN+\angle FMN=\angle AMB+\angle AEM+\angle BFM$$ $$=\angle AMB+\angle BAM+\angle ABM=180^o,$$ oleh karena itu $MEN’F$ siklik. Karena jari-jari lingkaran $\Delta MEF$ adalah $\Delta EN’F$. Karena $ENFN’$ jajargenjang, maka $\Delta EN’F\cong \Delta ENF$, jadi jari-jari lingkaran dari $\Delta EN’F$ sama dengan $\Delta NEF$. - $M$ adalah pusat segitiga sama sisi $A_1A_2A_3$, $N$ adalah titik sembarang pada bidang tempat segitiga tersebut berada, lingkaran dengan diameter $MN$ memotong garis $MA_i$ di $B_i$, $i=1,2,3$.
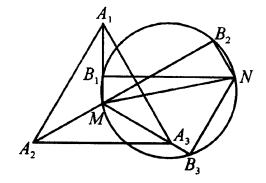
Buktikan bahwa $$MB_1^2+MB_2^2+MB_3^2=NB_1^2+NB_2^2+NB_3^2.$$
Solusi: Lima titik $M,B_1,B_2,N,B_3$ konsiklik dan $\angle B_1MB_3 =120^o$, maka $\angle B_1B_2B_3=60^o$ dan $$\angle B_1B_3B_2=\angle B_1MB_2=\angle A_1MB_2=60^o,$$ oleh karena itu $\Delta B_1B_2B_3$ sama sisi. Misalkan $s$ menjadi panjang sisinya.
Lemma: Jika $P$ adalah titik pada lingkaran luar segitiga sama sisi $ABC$, maka nilai dari $$PA^2+PB^2+PC^2$$ tidak tergantung pada pilihan $P$.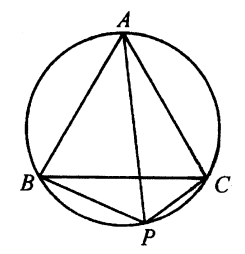
Faktanya, misalkan $a$ panjang dari $AB,PA=x,PB=y,PC=z$, maka $x=y+z$, oleh karena itu dengan menerapkan aturan kosinus, $$x^2+y^2+z^2=(y+z)^2+y^2+z^2=2(y^2+z^2+yz)$$ $$=2BC^2=2a^2,$$ Lemma terbukti, Dengan lemma, $$MB_1^2+MB_2^2+MB_3^2=NB_1^2+NB_2^2+NB_3^2=2s^2.$$ - Misalkan $A,B$ menjadi dua titik tetap dan $C$ adalah titik variable sehingga $\Delta ACB=\alpha$ yang konstan dan $0^o<\alpha <180^o$. Misalkan $D,E,F$ merupakan proyeksi titik pusat $I$ pada $ABC$ masing-masing sisi-sisinya $BC, CA, AB$. Nyatakan dengan $M, N$ perpotongan garis $AI, BI$ dengan ruas garis $EF$, masing-masing. Buktikan bahwa panjang $MN$ konstan dan lingkaran luar $\Delta DMN$ selalu melalui suatu titik tetap.
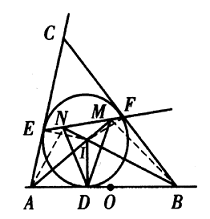
Solusi: Karena $\angle CEF=90^o-\frac{1}{2}\angle C=180^o-\angle AIB=\angle AIN$, jadi $I,N,E,A$ konsiklik. Maka $I,E,A,D$ konsiklik, begitu juga $I,N,E,A,D$ adalah konsiklik.
Demikian pula, $B,F,M,I,D$ konsiklik. Oleh karena itu, $$\angle ANB=\angle AEI=90^o,\angle AMB=\angle BFI=90^o.$$ Maka $M,N$ keduanya berada pada lingkaran dengan mengambil $AB$ sebagai diameternya. Mengambil $O$ sebagai titik tengah $AB$, maka $\angle MON=2\angle MAN=2\angle MBN=\angle MAN+\angle MBN=\angle NDI+\angle MDI=\angle MDN$, maka $M,N,D,O$ konsiklik, jadi lingkaran luar $\Delta MND$ melalui suatu titik tetap $O$.
Di sisi lain, $$MN=AB\sin \angle NAM=AB\sin \angle IEF=AB\sin\frac{C}{2}$$ yang merupakan konstanta. - Misalkan $X,X_1,X_2$ menjadi titik di sisi $AB,AC,BC$ dari $\Delta ABC$, sehingga $XX_1\bot AC,X_1X_2\bot BC,X_2X\bot AB$. Misalkan $Y,Y_1,Y_2$ menjadi titik pada $BC,AC,AB$, sehingga $YY_1\bot AC,Y_1Y_2\bot AB$. Buktikan bahwa $Y_2Y\bot BC$ jika $XY||AC$.
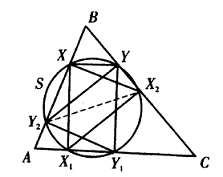
Solusi: Seperti yang di tunjukkan pada gambar, ketika $XY||AC$, maka $\angle YXX_1=\angle XX_1Y_1=90^o$. Mengingat $\angle X_1X_2Y=90^o$ maka diperoleh bahwa $X,X_1,X_2,Y$ konsiklik dan $X_1Y$ adalah diameter lingkaran. Menggunakan $\Gamma$ untuk menyatakan lingkaran.
Karena $\angle YY_1X_1=90^o$, maka $Y_1$ juga ada dalam $\Gamma$.
Karena $\angle XY_2Y_1=90^o$ dan $\angle XYY_1=90^o$, maka $X,Y_2,Y_1,Y$ konsiklik. Oleh karena itu $Y_2$ ada dalam $\Gamma$ juga.
Karena $\angle X_2XY_2=90^o$, maka $X_2Y_2$ adalah diameter $\Gamma$. Jadi, $$\angle Y_2YX_2=90^o\Rightarrow Y_2Y\bot BC.$$
Solusi dari setiap Permasalahan diberikan pada kelas online
“Leadership is the art of getting someone else to do something you want done because he wants to do it.”

