Pertidaksamaan Geometri

- Contoh Soal
Dalam bab ini, kita membahas pertidaksamaan yang berkaitan dengan panjang segmen, ukuran
sudut, dan ukuran luas grafik geometri. Teorema-teorema berikut merupakan
alat dasar untuk menangani pertidaksamaan geometri:
Teorema I. Di antara lintasan yang menghubungkan dua titik tertentu, segmen yang menghubungkan keduanya adalah yang terpendek.
Teorema II. Untuk garis lurus $\mathscr{l}$ dan titik $P$ di luar $\mathscr{l}$, jika $Q$ adalah kaki garis tegak lurus dari $P$ ke $\mathscr{l}$, dan $A, B$ adalah dua titik lain pada $\mathscr{l}$, sehingga $AQ < BQ$, maka $PQ < PA < PB$.
Teorema III (Pertidaksamaan Segitiga). Untuk sembarang segitiga $ABC$, misalkan $BC = a, CA =b, AB = c$, maka $a < b + c,$ $b < c + a,$ $c < a + b$, atau ekuivalennya, $a > |b − c|, b >|c − a|, c > |a − b|$.
Teorema IV. Pada segitiga, sisi yang lebih panjang berhadapan dengan sudut yang lebih besar, sisi yang lebih pendek berhadapan dengan sudut yang lebih kecil, dan sebaliknya.
Teorema V. Untuk setiap segitiga, median salah satu sisinya kurang dari setengah jumlah dua sisi lainnya.
Contoh Soal
- Diketahui titik $R$ merupakan titik dalam $\Delta ABC$, buktikan bahwa $AB + AC > BR + RC$.
Solusi: Memperluas $BR$ hingga berpotongan dengan $AC$ di $S$.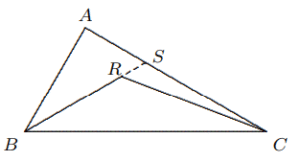
Maka $$AB + AC = AB + AS + SC$$ $$> BS + SC = BR + (RS + SC)$$ $$> BR + RC.$$ - Misalkan $AB$ dan $CD$ adalah dua ruas garis dengan panjang $1$. Jika keduanya berpotongan di $O$ sehingga $∠AOC = 60◦$, buktikan bahwa $AC + BD ≥ 1$.
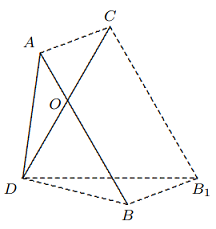
Solusi: Hubungkan $AC, BD$, dan masukkan $CB_1 || AB$, dengan $CB_1 = AB$. Maka $ABB_1C$ adalah jajargenjang, jadi $BB_1 = AC$. Hubungkan $B_1D$. Maka $\Delta CDB_1$ adalah sama sisi. Menerapkan pertidaksamaan segitiga ke $\Delta DBB_1$ menghasilkan $$AC + BD = BB1 + BD > DB1 = CD = 1,$$ sesuai keinginan.
Perhatikan bahwa ketika $A$ dan $C$ bertepatan, maka $AC + BD = BD = 1$. - Pada segi empat cembung $ABCD, ∠BAD =∠BCD = 90◦$, dan sinar $AK$ membagi dua $∠BAD$. Jika $AK || BC, AK ⊥ CD$, dan $AK$ berpotongan dengan $BD$ di titik $E$, buktikan bahwa $AE < \frac{1}{2}CD$.
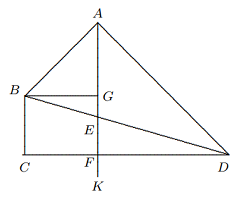
Solusi: Misalkan $AK$ berpotongan dengan $CD$ di $F$ dan $BG ⊥ AK$ di $G$. Maka $\Delta ABG$ dan $\Delta ADF$ keduanya merupakan segitiga siku-siku sama kaki, jadi $$BG = AG, F D = AF.$$ Karena $BCFG$ adalah persegi panjang, $FD = AF > AG = BG = CF$, jadi $$FD>\frac{1}{2}(CF+FD)=\frac{1}{2}CD,$$ $$∴ EF =\frac{FD}{CD}\cdot BC>\frac{1}{2}BC.$$ Karena $BC + CF = FD$, kita memiliki $$CD = CF + F D = 2F D − BC > 2(F D − EF) = 2(AF − EF) = 2AE,$$ yaitu $AE<\frac{1}{2}CD$. - Untuk $\Delta ABC$, misalkan $a = BC, b = CA, c = AB$. Jika $b < \frac{1}{2}(a + c)$, buktikan bahwa $∠B <\frac{1}{2}(∠A + ∠C)$.
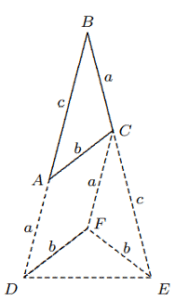
Solusi: Mengingat $∠A + ∠B + ∠C = 180◦$, $$∠B <\frac{1}{2}(∠A + ∠C) \Longleftrightarrow ∠B < 60◦.$$ Sekarang, buatlah segitiga sama kaki $BDE$ dengan memanjangkan $BA$ ke $D$ dan memanjangkan $BC$ ke $E$, sehingga $BD = c +a,$ $BE = a + c$. Selanjutnya, kita buat jajargenjang $ACFD$ sehingga $AC || DF, AD || CF$, maka $$\Delta BAC \cong \Delta CFE, ∴ FE = AC = FD = b.$$ Dari $DE < DF + FE = 2b < a + c$, maka $DE < BE = BD,$ Oleh karena itu, $∠B < ∠E$, yaitu $2B < 180◦ − B$, atau $∠B < 60◦$. Kesimpulannya adalah terbukti. - Diketahui sisi terpanjang $AC$ dari $\Delta ABC$ memenuhi persamaan $AC > BC$. Jika titik $M$ berada pada perpanjangan $AC$ sehingga $CM = BC$. Buktikan bahwa $∠ABM > 90◦$.
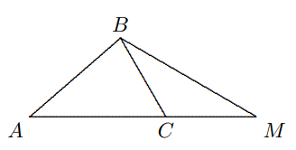
Solusi: $∠AC > BC$ menyiratkan $∠ABC > ∠A$. Hubungkan $BM$. Kemudian $$∠ABM = ∠ABC + ∠CBM$$ $$=\frac{1}{2}∠ABC +\frac{1}{2}∠ABC +\frac{1}{2}∠ACB$$ $$=\frac{1}{2}∠ABC −\frac{1}{2}∠A + 90◦ > 90◦.$$ Jadi, $∠ABM$ tumpul. - Diketahui dua segiempat cembung $ABCD$ dan $A’B’C’D’$ memiliki sisi-sisi yang bersesuaian sama besar, yaitu $AB = A’B’, BC = B’C’$, dst. Buktikan bahwa jika $∠A > ∠A0,$ maka $∠B < ∠B’, ∠C > ∠C’, ∠D < ∠D’$.
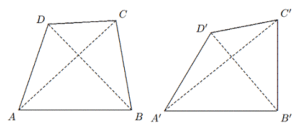
Solusi: Pada $\Delta ABD$ dan $\Delta A’B’D’, AB = A’B’, AD = A’D’, ∠A > ∠A’$ menghasilkan $BD > B’D’$. Pada $\Delta BCD$ dan $\Delta B’C’D’, BC = B’C’, CD = C’D’$ dan $BD > B’D’$ menunjukkan $∠C > ∠C’$.
Oleh karena itu, $∠B + ∠D < ∠B’ + ∠D’$. Misalkan $∠B ≥ ∠B’$, maka $∠D < ∠D’$, sehingga dengan penalaran yang sama, $∠B’ > ∠B$, sebuah kontradiksi. Dengan demikian, $∠B < ∠B’$ dan $∠D < ∠D’$, sesuai keinginan. - Misalkan $ABC$ adalah sebuah segitiga. Buktikan bahwa terdapat garis $\mathscr{l}$ (pada bidang segitiga $ABC$) sehingga perpotongan antara bagian dalam segitiga $ABC$ dan bagian dalam refleksinya $A’B’C’$ di $\mathscr{l}$ memiliki luas lebih dari $2/3$ luas segitiga $ABC$.
Solusi: Misalkan $BC = a, CA = b, AB =c$. Tanpa mengabaikan keumuman, kita dapat mengasumsikan bahwa $a ≤ b ≤ c$. Misalkan $AD$ adalah garis bagi sudut $∠BAC, B’, C’$ masing-masing adalah titik-titik simetris $B, C$ pada garis $AD$, maka $C’$ berada pada ruas garis $AB$ dan $B’$ berada pada perpanjangan $AC$, seperti yang ditunjukkan pada gambar.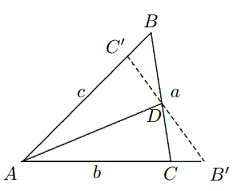
Dari $$[BDC’]=\frac{BC’}{AB}\cdot \frac{BD}{BC}\cdot [ABC]=\frac{c-b}{c}\cdot \frac{c}{b+c}[ABC]=\frac{c-b}{b+c}[ABC].$$ $2b>a+b>c$ menyiratkan $\frac{b}{c+b}>\frac{b}{2b+b}=\frac{1}{3}$, maka $$[AC’DC]=\left(1-\frac{c-b}{c+b}\right)[ABC]=\frac{2b}{c+b}[ABC]>\frac{2}{3}[ABC].$$ Dengan demikian, baris $AD$ memenuhi persyaratan. - Melalui titik berat $G$ dari $\Delta ABC$, buatlah garis yang membagi $\Delta ABC$ menjadi dua bagian. Buktikan bahwa selisih luas kedua bagian tersebut tidak lebih besar dari $\frac{1}{9}$ luas $\Delta ABC$.
Solusi:
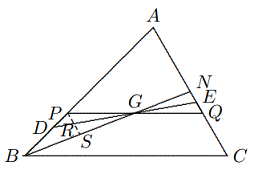
Misalkan suatu garis sembarang yang melalui $G$ memotong $AB$ dan $AC$ masing-masing di titik $D$ dan $E$. Jika garis $DE$ sejajar dengan $BC$, maka $$[ADE]=\left(\frac{DE}{BC}\right)^2[ABC]=\frac{4}{9}[ABC],\text{ maka}$$ $$|[ADE] − [DBCE]| =\left(\frac{5}{9}-\frac{4}{9}\right)[ABC]$$ $$=\frac{1}{9}[ABC],\text{ kesimpulannya benar.}$$ Ketika $DE$ tidak sejajar dengan $BC$, katakanlah $D$ berada di antara $P$ dan $B$ dan $E$ berada di antara $Q$ dan $N$, di mana $PQ || BC$ dan $N$ adalah titik tengah $AC$, seperti yang ditunjukkan pada gambar, kita menunjukkan bahwa $$|[DBCE] − [ADE]| < |[PBCQ] − [APQ]| =\frac{1}{9}[ABC]$$ di bawah ini. Karena $∠DPG > ∠PQA$, kita dapat memperkenalkan $PS || AC$, yang memotong $DE$ dan $BN$ masing-masing di $R$ dan $S$. Maka $\Delta PRG \cong \Delta QEG$ dan $\Delta RSG \cong \Delta ENG$, sehingga $$[PRG] = [QEG] \text{ dan } [RSG] = [ENG].$$ Oleh karena itu $[DBCE] = [PBCQ] − [PDG] + [QEG] < [PBCQ]$ dan $[ADE] =
[APQ] + [PDG] − [QEG] > [APQ]$, sehingga $$[DBCE] − [ADE] < [PBCQ] − [APQ] =\frac{1}{9}[ABC].$$ Cukup untuk menunjukkan bahwa $[DBCE] > [ADE]$. Untuk pemberitahuan ini bahwa $$[DBCE] = [BCN] − [ENG] + [DBG] > [BCN] − [ENG] + [RSG]$$ $$= [BCN] = \frac{1}{2}[ABC],$$ $$∴ [ADE] <\frac{1}{2}[ABC] < [DBCE].$$ Dengan demikian, kesimpulannya terbukti. - Misalkan $\Delta ABC$ adalah segitiga siku-siku sama kaki yang sisi-sisinya sama panjang $1$. $P$ adalah sebuah titik pada hipotenusa, dan kaki-kaki garis tegak lurus dari $P$ ke sisi-sisi lainnya adalah $Q$ dan $R$. Perhatikan luas segitiga $APQ$ dan $PBR$, dan luas persegi panjang $QCRP$. Buktikan bahwa terlepas dari bagaimana $P$ dipilih, luas terbesar dari ketiga luas ini setidaknya $\frac{2}{9}$.
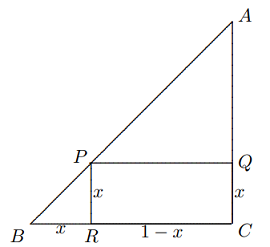
Solusi: Misalkan $BR = x$, maka $BR = PR = QC = x$ dan $RC = PQ = AQ = 1 − x$.
(i) Ketika $x\ge \frac{2}{3}$, maka $$[PBR]=\frac{x^2}{2}\ge \frac{2}{9}.$$
(ii) Ketika $x\le \frac{1}{3}$, maka $1-x\ge \frac{2}{3}$, sehingga $$[APQ]=\frac{(1-x)^2}{2}\ge \frac{2}{9}$$
(iii) Ketika $\frac{1}{3}<x<\frac{2}{3}$, maka $-\frac{1}{6}<x-\frac{1}{2}<\frac{1}{6}$, sehingga $$[QCRP]=x(1-x)=-x^2+x=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}>-\frac{1}{36}+\frac{1}{4}=\frac{2}{9}.$$ Dengan demikian, kesimpulannya terbukti.
Solusi dari setiap Permasalahan diberikan pada kelas online
“The greatest discovery of all time is that a person can change his future by merely changing his attitude.”

