Persamaan Segitiga

- Kriteria Kesebangunan Dua Segitiga
- Sifat Dasar Dua Segitiga Sebangun
- Sifat Proporsional Penting dari Segmen
- Contoh Soal
Dua segitiga disebut kongruen jika kita bisa mendapatkan dua segitiga yang kongruen setelah memperbesar atau mempersempit sisi-sisi salah satunya dengan perbandingan yang sama. Artinya, dua segitiga kongruen berarti memiliki bentuk yang sama tetapi mungkin memiliki ukuran yang berbeda.
Kriteria Kesebangunan Dua Segitiga
(I) Setiap pasangan sudut yang bersesuaian sama besar (A.A.A.);
(II) Semua sisi yang bersesuaian proporsional (S.S.S.);
(III) Dua pasang sisi yang bersesuaian adalah proporsional, dan sudut-sudut yang bersesuaian yang disertakan adalah sama besar (S.A.S.);
(IV) Untuk dua segitiga siku-siku, sepasang dua sudut lancip yang bersesuaian adalah sama besar (A.A.);
(V) Di antara tiga pasang sisi yang bersesuaian, dua pasang adalah yang proporsional (S.S.).
Sifat Dasar Dua Segitiga Sebangun
(I) Untuk dua segitiga sebangun, sisi-sisi yang bersesuaian, tinggi yang bersesuaian, garis beraturan yang bersesuaian, garis bagi sudut yang bersesuaian, keliling yang bersesuaian semuanya proporsional dengan rasio yang sama.
(II) Anggaplah keserupaan sebagai transformasi dari satu segitiga ke segitiga lainnya, maka transformasi ini mempertahankan banyak fitur grafik yang tidak berubah: setiap sudut interior tidak berubah; dua garis sejajar tetap sejajar, sudut yang dibentuk oleh dua garis yang berpotongan tetap tidak berubah, dan titik-titik kolinear tetap kolinear.
(III) Untuk dua segitiga sebangun, rasio luasnya sama dengan kuadrat rasio sisi-sisi yang bersesuaian.
Sifat Proporsional Penting dari Segmen
Ketika kita menyatakan panjang segmen dengan $a, b, c, …,$ maka berlaku sifat-sifat proporsional berikut, yang sama seperti dalam aljabar:
(1) $\frac{a}{b}=\frac{c}{d}\Longrightarrow ad=bc;$
(2) $\frac{a}{b}=\frac{c}{d}\Longrightarrow \frac{a+b}{b}=\frac{c+d}{d};$
(3) $\frac{a}{b}=\frac{c}{d}\Longrightarrow \frac{a-b}{b}=\frac{c-d}{d};$
(4) $\frac{a}{b}=\frac{c}{d}\Longrightarrow \frac{a+b}{a-b}=\frac{c+d}{c-d}\text{ jika }a-b\neq 0\text{ atau }c-d\neq 0;$
(5) $\frac{a}{b}=\frac{c}{d}=…=\frac{m}{n}(bd…n\neq 0)\Longrightarrow \frac{a+c+…+m}{b+d+…+n}=\frac{a}{b}=\frac{c}{d}=…=\frac{m}{n}\text{ jika }b+d+…+n\neq 0.$
Contoh Soal
- Buktikan hal berikut:
(1) Ketika dua garis lurus dipotong oleh tiga garis sejajar, kedua ruas garis di antara dua garis sejajar yang berdekatan adalah proporsional.
(2) Ketika sebuah garis lurus yang sejajar dengan salah satu sisi segitiga memotong sisi-sisi segitiga lainnya di dua titik, ketiga sisi segitiga turunan harus proporsional dengan ketiga sisi segitiga asal, secara koresponden.Solusi: (1) Jika dua garis $\mathscr{l}_1$ dan $\mathscr{l}_2$ sejajar, kesimpulannya jelas.
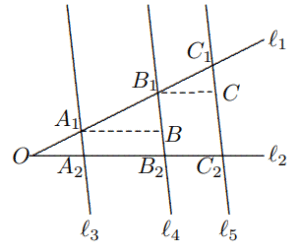
Jika $\mathscr{l}_1 ∦ \mathscr{l}_2$, misalkan $O$ adalah titik potongnya. Jika tiga garis sejajar $\mathscr{l}_3, \mathscr{l}_4, \mathscr{l}_5$ berpotongan $\mathscr{l}_1$ dan $\mathscr{l}_2$ di $A_1, B_1, C_1$ dan $A_2, B_2, C_2$ secara berurutan, seperti yang ditunjukkan pada diagram di sebelah kanan, misalkan $$A_1B||\mathscr{l}_2,\text{ berpotongan }\mathscr{l}_4\text{ di }B,$$ $$B_1C||\mathscr{l}_2,\text{ berpotongan }\mathscr{l}_5\text{ di }C,$$ maka $A_1A_2B_2B$ dan $B_1B_2C_2C$ adalah jajargenjang, $$∴ A_1B = A_2B_2, B_1C = B_2C_2. \text{ }∵ \Delta A_1BB_1 ∼ \Delta B_1CC_1 \text{ (A.A.A.)},$$ $$∴\frac{A_1B_1}{B_1C_1}=\frac{A_1B}{B_1C}.\text{ Maka }\frac{A_1B_1}{B_1C_1}=\frac{A_2B_2}{B_2C_2}.$$
(2) Diberikan $\Delta ABC$. Jika garis $\mathscr{l}||BC$, berpotongan dengan $AB, AC$ di $B_1, C_1$ berturut-turut. Maka $$∠AB_1C_1 = ∠ABC, ∠AC_1B_1 = ∠ACB,$$ $$∴ \Delta AB_1C_1 ∼ \Delta ABC \text{ (A.A.A.)},$$ Oleh karena itu, sisi-sisi kedua segitiga tersebut proporsional. - (Teorema Garis Bagi Sudut) Untuk setiap segitiga, garis bagi sudut dari setiap sudut dalam harus memotong sisi yang berhadapan menjadi dua segmen, sehingga rasionya sama dengan rasio kedua sisi sudut tersebut.
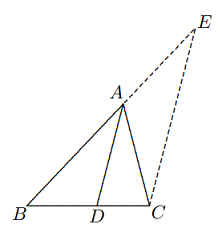
Solusi: Pada $\Delta ABC$, misalkan $AD$ adalah garis bagi sudut $∠BAC$, di mana $AD$ dan $BC$ berpotongan di $D$.
Dari $C$, masukkan $CE || AD$, yang memotong perpanjangan $BA$ di $E$. Maka $$∠ECA = ∠DAC = ∠BAD$$ $$= ∠AEC, ∴ AC = AE.$$ $$∵ AD || EC,$$ $$∴ \frac{AB}{AE}=\frac{BD}{CD},$$ $$∴\frac{AB}{AC}=\frac{BD}{CD}.$$ Catatan: Ketika $AD$ adalah garis bagi sudut luar sudut $BAC$, demikian pula, berlaku juga bahwa $$\frac{AB}{AC}=\frac{BD}{CD}.$$ - (Teorema Proyeksi Segitiga Siku-siku) Pada segitiga siku-siku $ABC, ∠ACB = 90◦$. Maka $$CD^2 = AD \cdot DB,\text{ }\text{ } AC^2 = AD \cdot AB, \text{ }\text{ }BC^2 = BD \cdot BA.$$
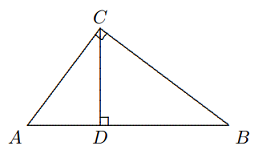
Solusi: Dari $∠ACD = 90◦ − ∠A = ∠CBD$, maka Rt$\Delta ACD ∼$ Rt$\Delta CBD$ (A.A.A.), kita peroleh $$\frac{CD}{AD}=\frac{BD}{CD},$$ yaitu $CD^2=AD\cdot BD$. $$∵ ∠CAD = ∠BAC, ∴ \text{Rt}\Delta CAD ∼ \text{Rt}\Delta BAC$$ $$∴\frac{AC}{AD}=\frac{AB}{AC},\text{ yaitu }AC^2=AD\cdot AB$$ Bukti $BC^2 = BD \cdot BA$ serupa. - (Teorema Sentroid) Untuk setiap segitiga $ABC$, ketiga garis tengahnya harus berpotongan di satu titik persekutuan $G$, dan setiap garis tengah dibagi oleh $G$ menjadi dua segmen dengan rasio $2 : 1$.
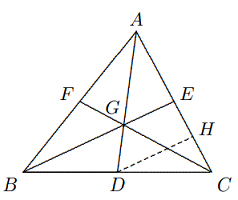
Solusi: Misalkan $G$ adalah titik potong median $AD$ dan $BE$. Dari $D$, masukkan $DH || BE$, sehingga $DH$ berpotongan dengan $AC$ di $H$. Dengan teorema titik tengah, $$AE=EC=2CH=2HE.$$ $$∵ \Delta AGE ∼ \Delta ADH,$$ $$∴\frac{AG}{GD}=\frac{AE}{EH}=2.$$ Demikian pula, $\frac{BG}{GE}=2$.
Misalkan $CF$ berpotongan dengan $AD$ di $G’$, maka, seperti pembuktian di atas, $\frac{AG\text{ }’}{G\text{ }’D}= 2$, maka $G = G’$. Dengan demikian, $AD, BE$, dan $CF$ konkuren di $G$. - Pada $\Delta ABC, AD$ adalah median pada $BC, E$ adalah pada $AD$ sehingga $BE = AC$. Garis $BE$ berpotongan dengan $AC$ di $F$. Buktikan bahwa $AF = EF$.
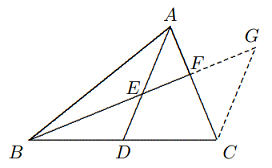
Solusi: Dari $C$ masukkan $CG || AD$, yang memotong perpanjangan $BF$ di $G$. $$∵ ∠EAF = ∠FCG,$$ $$∠AEF = ∠FGC,$$ $$∠AFE = ∠GFC,$$ $$∴ \Delta EAF ∼ \Delta GCF \text{ (A.A.A.)}.$$ $$∴\frac{AF}{EF}=\frac{FC}{FG}=\frac{AF+FC}{EF+FG}=\frac{AC}{EG}.$$ Dengan teorema titik tengah, $BE = EG,$ $$∴ EG = AC, AF = EF.$$ - Pada $\Delta ABC, AD, BE$ masing-masing adalah median pada $BC, AC$. Jika $∠CAD = ∠CBE = 30◦$, buktikan bahwa $\Delta ABC$ sama sisi.
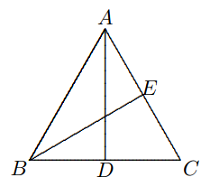
Solusi: $∵ \Delta ADC ∼ \Delta BEC$ (A.A.A.), oleh karena itu $$\frac{AC}{BC}=\frac{DC}{EC}=\frac{2DC}{2EC}=\frac{BC}{AC},$$ $$∴ AC^2 = BC^2, \text{ }AC = BC.$$ Pada $\Delta BEC, ∠BEC = 30◦, EC =\frac{1}{2}BC$. $$∴ ∠BEC = 90◦, ∠C = 60◦.$$ $$∴ \Delta ABC\text{ adalah sama sisi}.$$ - Pada $\Delta ABC, ∠A : ∠B : ∠C = 1 : 2 : 4$. Buktikan bahwa $$\frac{1}{AB}+\frac{1}{AC}=\frac{1}{BC}.$$
Solusi: Cukup dengan menunjukkan $\frac{AB + AC}{AB} = \frac{AC}{BC}$. Untuk membuktikannya, kita buatlah segitiga sebangun yang bersesuaian sebagai berikut.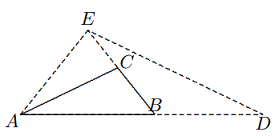
Perluas $AB$ ke $D$ sehingga $BD = AC$. Perluas $BC$ ke $E$ sehingga $AC = AE$. Hubungkan $DE, AE$. Misalkan $$∠A = α, ∠B = 2α, ∠C = 4α.$$
Maka $7α = 180◦.$
$∵ ∠AEC = ∠ACE = 3α,$
$∠CAE = α = ∠CAB,$
$∠BAE = 2α = ∠EBA.$
$∵ ∠DBE = ∠BAE + ∠AEB = 5α,$
$∴ ∠EDA =\frac{1}{2}(180◦ − 5α) = α,$
$∴ \Delta DAE ∼ \Delta ABC$ (A.A.A.).
Maka, $$\frac{AD}{AB}=\frac{EC}{BC},\text{ yaitu }\frac{AB+AC}{AB}=\frac{AC}{BC},\text{ sesuai keinginan. }$$ - $P$ adalah titik dalam dari $\Delta ABC, BC = a, CA = b, AB = c$. Melalui $P$, masukkan $IF || BC, DG || AB$, dan $EH || CA$ secara berurutan, di mana $I, H$ berada pada $AB, D, E$ berada pada $BC, F, G$ berada pada $CA$, seperti yang ditunjukkan pada diagram di bawah ini. Diketahui $DE = a’, FG = b’, HI = c’$, tentukan nilai $\frac{a’}{a}+\frac{b’}{b}+\frac{c’}{c}$.
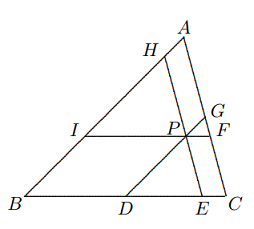
Solusi: Dari $IF||BC,HE||AC$ kita punya $\Delta HIP~\Delta ABC$, maka $$\frac{c’}{c}=\frac{IP}{a}=\frac{BD}{a}.$$ Karena $\Delta GPS~\Delta ABC$, $$\frac{b’}{b}=\frac{PF}{a}=\frac{EC}{a}.$$ Oleh karena itu $$\frac{a’}{a}+\frac{b’}{b}+\frac{c’}{c}=\frac{DE}{a}+\frac{BD}{a}+\frac{EC}{a}$$ $$=\frac{DE+BD+EC}{BC}=1$$ - Pada diagram di atas, $\Delta PQR$ dan $\Delta P’Q’R’$ merupakan dua segitiga sama sisi yang kongruen. Nyatakan panjang sisi segi enam $ABCDEF$ dengan $AB=a_1,BC=b_1,CD=a_2,DE=b_2,EF=a_3,FA=b_3.$ Buktikan bahwa $a_1^2+a_2^2+a_3^2=b_1^2+b_2^2+b_3^2$.
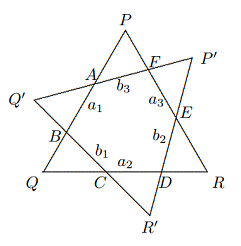
Solusi: Untuk dua segitiga yang berdekatan di luar segi enam yang tumpang tindih, misalnya $\Delta Q’AB$ dan $\Delta PAF$, kita memiliki $$∠P=∠Q’ = 60◦, ∠PAF = ∠Q’AB,$$ Oleh karena itu, $\Delta Q’AB ∼ \Delta PAF$. Demikian pula, setiap dua segitiga yang berdekatan adalah sebangun. Misalkan $$S_1=[Q’AB],S_2=[QBC],S_3=[R’CD]$$ $$S_4=[RDE],S_5=[P’FE],S_6=[PAF].$$ Maka $S_1 + S_3 + S_5 = S_2 + S_4 + S_6$. Gunakan $A$ untuk menyatakan jumlah umum di atas, maka $$\frac{b_1^2}{a_1^2}=\frac{S_2}{S_1},\frac{b_2^2}{a_1^2}=\frac{S_4}{S_1},\frac{b_3^2}{a_1^2}=\frac{S_6}{S_1}.$$ Dengan menjumlahkannya, kita memperoleh $$\frac{b_1^2+b_2^2+b_3^2}{a_1^2}=\frac{A}{S_1},∴a_1^2\cdot A=(b_1^2+b_2^2+b_3^2)S_1.$$ Demikian pula, kita punya $$a_2^2\cdot A=(b_1^2+b_2^2+b_3^2)S_2\text{ dan }a_3^2\cdot A=(b_1^2+b_2^2+b_3^2)S_3.$$ Dengan menambahkan ketiga persamaan ini, kita memperoleh $$(a_1^2+a_2^2+a_3^2)A=(b_1^2+b_2^2+b_3^2)(S_1+S_2+S_3)=(b_1^2+b_2^2+b_3^2)A,$$ $$∴a_1^2+a_2^2+a_3^2=b_1^2+b_2^2+b_3^2,\text{ sesuai keinginan}.$$
Solusi dari setiap Permasalahan diberikan pada kelas online
“Setting goals is the first step in turning the invisible into the visible.”

