Persamaan Diophantine (III)
Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Definisi
- Contoh Soal
Definisi
Dalam catatan Bab untuk bagian Junior, kita membahas persamaan Diophantine linear dan kuadrat. Dalam Bab ini, kita akan membahas persamaan Diophantine non-linier umum.
Seperti yang ditunjukkan dalam pembahasan persamaan Diophantine kuadrat, kita memiliki metode umum berikut untuk menyelesaikan persamaan Diophantine non-linier.
- Menggunakan manipulasi aljabar: termasuk menggunakan pelengkapan kuadrat, faktorisasi, substitusi variabel atau ekspresi.
- Estimasi dengan menggunakan pertidaksamaan: tujuannya adalah untuk menentukan rentang yang sempit untuk variabel.
- Menggunakan berbagai alat dalam teori bilangan: termasuk penggunaan pembagian, analisis paritas, kongruensi, berbagai teorema tentang kongruensi, residu kuadrat.
- Teknik keturunan tanpa batas.
- Metode konstruksi: Berdasarkan kondisi yang diberikan, konstruksikan solusi khusus yang memenuhi syarat atau rumus rekursif untuk suatu solusi.
Di sini, induksi matematika terkadang merupakan alat yang berguna.
Biasanya terdapat tiga jenis pertanyaan yang melibatkan persamaan Diophantine: (1) Untuk menemukan solusinya; (2) untuk menentukan apakah persamaan tersebut memiliki solusi yang diperlukan; dan (3) untuk menentukan apakah persamaan yang diberikan memiliki solusi yang terbatas atau tak terhingga.
Contoh Soal
- Temukan semua bilangan bulat $x$ sehingga $x (x + 1)(x + 7)(x + 8)$ merupakan kuadrat sempurna.
Solusi: Kami ingin menemukan semua pasangan bilangan bulat terurut $(x, y)$ yang memenuhi $$x(x + 1)(x + 7)(x + 8) = y^2 (x ∈ \mathbb{Z}, y ∈ \mathbb{N}_o).$$ Misalkan $z=x+4$, maka $$x(x + 1)(x +7)(x + 8) = y^2 \Rightarrow (z – 4)(z- 3)(z +3)(z +4) = y^2$$ $$\Rightarrow (z^2-16)(z^2-9) = y^2 \Rightarrow z^4-25z^2 +12^2 = y^2$$ $$\Rightarrow (2z^2)^2- 50(2z^2) +25^2 – (2y)^2 = 49$$ $$\Rightarrow (2z^2 – 25)^2 – (2y)^2 = 49$$ $$\Rightarrow (2z^2 -25-2y)(2z^2-25+2y) = 49.$$ Dari $49 = (-49)(−1) = (−7)(–7) = 1·49 = 7· 7,$ empat sistem dengan dua persamaan simultan dapat diperoleh: $$\left\{ \begin{array}{cl}
2z^2-25-2y & =-49, \\
2z^2-25+2y & =-1;
\end{array} \right.\text{ atau }\left\{ \begin{array}{cl}
=-7, \\
=-7;
\end{array} \right.\text{ atau }\left\{ \begin{array}{cl}
=1, \\
=49;
\end{array} \right.\text{ atau }\left\{ \begin{array}{cl}
=7, \\
=7;
\end{array} \right.$$ Misalkan $A = 2z^2 – 25 – 2y, B = 2z^2 – 25 + 2y$, solusi untuk $(y, z)$ dan kemudian untuk $x$ diperoleh dengan mudah seperti yang ditunjukkan pada tabel berikut: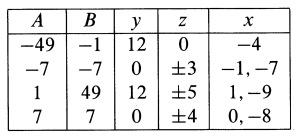
di mana nilai $y, z, x$ diperoleh dengan $B- A = 4y, 2z^2 = 25+A+2y, x =z – 4$. Dengan memeriksa, semua nilai yang diperoleh untuk $x$ adalah solusi. - Temukan semua pasangan terurut $(m, n) (m, n > 1)$ bilangan bulat positif sehingga $n^3 – 1$ habis dibagi $mn – 1$.
Solusi: Misalkan $m, n > 1$ adalah bilangan bulat positif yang memenuhi $(mn – 1) | (n^3 — 1)$.
Karena $(n^3 – 1)m – n^2(mn – 1) = n^2 – m$, maka $(mn- 1) | (n^2 – m)$. Selanjutnya, $$m(n^2-m) – (mn – 1)n = n -m^2 \Rightarrow (mn – 1) | п – m^2.$$
(i) Jika $n > m^2$, maka $mn – 1 ≤ n − m^2 ≤ n – 1$, tidak ada solusi.
(ii) Jika $n = m^2$, maka $(m^3 – 1) | (m^6 – 1)$ menyiratkan bahwa semua pasangan bilangan bulat dengan bentuk $(m, m^2)$, $m > 1$ memenuhi persyaratan.
(iii) Jika $n < m^2$, maka $mn – 1 ≤ n^3 -1\Rightarrow \sqrt{n} < m ≤ n^2$. Jika $m < n^2$, maka $mn -1 ≤ n^2 -m < n^2 -1 ⇒ m < n$, tetapi kemudian $mn -1 ≤ m^2 -n < m^2 -1 ⇒ n < m$, sebuah kontradiksi. Jadi, $m = n^2$.
Karena $(n^3 – 1) | (n^3 — 1)$ untuk setiap bilangan bulat positif $n > 1$, maka semua pasangan $(n^2, n), n > 1$ juga merupakan solusi.
Singkatnya, semua pasangan $(k, k^2)$ dan $(k^2, k)$ di mana $k > 1$ dan $k\in\mathbb{N}$ adalah solusinya. - Tentukan bilangan bulat positif $k_1, k_2,…, k_n$ dan $n$, sehingga $$k_1+ k_2+…+ k_n=5n-4\text{ dan }\frac{1}{k_1}+…+\frac{1}{k_n}=1.$$
Solusi: Berdasarkan ketidaksetaraan Cauchy-Schwartz, $$\left( \frac{1}{k_1}+\frac{1}{k_2}+…+\frac{1}{k_n} \right)(k_1+k_2+…+k_n)\ge n^2.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(22.1)$$ Oleh karena itu, $5n – 4 ≥ n^2$, dan dapat disimpulkan bahwa $1 ≤ n ≤ 4$. Persamaan tersebut berlaku jika dan hanya jika $k_1 = k_2 = … = k_n$ dan $n = 1$ atau $4$. Faktanya,
Ketika $n = 1$, maka $k = 1$.
Ketika $n = 4$, maka $k_1 = k_2 = k_3 = k_4 = 4$.
Ketika $n = 2$, maka $k_1 + k_2 = 6,\frac{1}{k_1}+\frac{1}{k_2} = 1 ⇒ k_₁k_2 = 6, k_1, k_2$ adalah akar-akar persamaan $t^2 – 6t +6 = 0$, sehingga merupakan bilangan irasional, tidak memerlukan solusi dalam kasus ini.
Ketika $n = 3$, maka $k_1 + k_2 + k_3 = 11, \frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}= 1$. Misalkan $k_1 ≤ k_2 \le k_3$, maka $$1=\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}\le \frac{3}{k_1}\Rightarrow k_1\le 3.$$ Jika $k_1=2$, maka $k_2+k_3=9,\frac{1}{k_2}+\frac{1}{k_3}=\frac{1}{2}\Rightarrow k_2=3,k_3=6.$
Jika $k_1=3$, maka $\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}=1$ dan $k_1\le k_2\le k_3$ menyiratkan $k_1=k_2=k_3=3$, yang kontradiksi dengan $k_1+k_2+k_3=11$, maka tidak ada solusi pada kasus ini.
Maka, bila $n = 3$, solusi untuk rangkap tiga terurut $(k_1, k_2, k_3)$ adalah $(2, 3,6)$ dan permutasinya. - Temukan semua tripel $(x, y, z)$ bilangan bulat positif sedemikian rupa sehingga $1+4^x+4^y=z^2$.
Solusi: Dengan simetris, kita bisa asumsikan bahwa $\le y$.
(i) Jika $2x < y + 1$, maka $(2^y)^2 < 1+4^x + 4^y < (1 + 2^y)^2$, yang menunjukkan bahwa $1+4^x + 4^y$ bukan kuadrat sempurna, tidak ada solusi dalam kasus ini.
(ii) Jika $2x = y + 1$, maka $1 + 4^x + 4^y = 1 + 2^{y+1} + 2^{2y} = (1 + 2^y)^2$, maka $(n, 2n -1, 1 + 2^{2n -1}), n ∈ \mathbb{N}$ adalah solusi.
(iii) Jika $2x > y + 1$, maka $x > 1$, maka $y ≥ x ≥ 2$ dan $4^x + 4^y = 4^x(1 + 4^{y-x}) = (z – 1)(z + 1)$. Karena FPB$(z – 1, z + 1) = 2$, salah satu dari $z – 1$ dan $z + 1$ habis dibagi $2^{2x – 1}$. Namun, $$2(1+4^{y-x})\le 2(1+4^{x-2})<2^{2x-1}-2,$$ sebuah kontradiksi. Jadi, tidak ada solusi dalam kasus ini. Kesimpulannya, $$(n,2n-1,1+2^{2n-1}),n\in\mathbb{N}\text{ atau }(2n-1,n,1+2^{2n-1}),n\in\mathbb{N}.$$ - Temukan semua bilangan bulat positif $n$, sedemikian rupa sehingga terdapat bilangan bulat bukan nol $x_1, x_2,…,x_n,y$ yang memenuhi sistem persamaan $$\left\{ \begin{array}{cl}
x_1+x_2+…+x_n & =0,\\
x_1^2+x_2^2+…+x_n^2 & =ny^2.
\end{array} \right.$$
Solusi: Jelas bahwa $n \neq 1$.
Jika $n = 2k, k ∈ \mathbb{N}$, misalkan $x_{2i-1} = 1, x_{2i} = -1, i = 1, 2,…, k$ dan $y = 1,$ persamaan tersebut terpenuhi.
Jika $n = 3+ 2k, k∈ \mathbb{N}$, misalkan $y = 2, x_1 = 4, x_2 = x_3 = x_4 =x_5= −1$, dan misalkan $$x_{2i}=2.x_{2i+1}=-2,\text{ atau }i=3,4,…,k+1,$$ maka persamaan tersebut terpenuhi.
Jika $n = 3$, misalkan ada bilangan bulat bukan nol $x_1, x_2, x_3$ dan $y$ sehingga $$\left\{ \begin{array}{cl}
x_1+x_2+x_3 & =0,\\
x_1^2+x_2^2+x_3^2 & =3y^2.
\end{array} \right.$$ maka $2(x_1^2+x_2^2+x_1x_2)=3y^2$. Karena dapat diasumsikan bahwa FPB$(x_1,x_2,x_3) = 1$, maka dapat diasumsikan bahwa $(x_1,x_2) = 1$. Maka $x_1^2+x_2^2+x_1x_2$ pasti ganjil ketika $x_1$ dan $x_2$ keduanya ganjil (karena $x_1$ dan $x_2$ tidak mungkin keduanya genap) atau satu ganjil dan satu genap. Namun, karena $y$ genap, maka $3y^2 =\equiv 0$ (mod $4$), sedangkan $2(x_1^2 + x_2^2+ x_1x_2) \neq 0$ (mod 4), sebuah kontradiksi.
Dengan demikian, semua bilangan asli kecuali $1$ dan $3$ memenuhi persyaratan pertanyaan. - Temukan semua solusi bilangan bulat positif dari persamaan $3^x -5^y = z^2$.
Solusi: Dengan mengambil modulo $4$ ke kedua sisi persamaan yang diberikan, $$z^2\equiv (-1)^x-1^y\equiv (-1)^x-1\text{ }(\text{mod }4)\Rightarrow z,x \text{ kedua nya genap}.$$ Misalkan $x=2t(t\in\mathbb{N})$, maka persamaan yang diberikan menjadi $$(3^t-z)(3^t+z)=5^y.$$ Oleh karena itu ada $k ∈ \mathbb{N}_0$ sehingga $3^t – z = 5k, 3^t + z = 5^{y-k}$, maka $$5^k+5^{y-k}=2(3^t)\Rightarrow k=0\Rightarrow 2(3^t)=5^y+1.$$ Ketika $t ≥ 2$, maka $5^y + 1 \equiv 0$ (mod $9$)$\Leftrightarrow y\equiv 3$ (mod $6$) karena $5^6 \equiv 1$ (mod $9$) dan $5^3 \equiv 8$ (mod $9$), dan dalam kasus ini $5^y + 1 \equiv 5^3 + 1\equiv 0$ (mod $7$) karena $5^6 \equiv 1$ (mod $7$). Jadi, $7 | (5^y + 1)$, sedangkan $7\nmid 2(3^t)$, tidak ada solusi dalam kasus ini.
Ketika $t ≤ 1$, maka $t = 1$, yang menyiratkan bahwa $y = 1, x = 2, z = 2$. Dengan demikian, (2, 1, 2) adalah solusi unik. - Temukan semua pasangan bilangan bulat positif yang terurut $(m, n)$, sehingga $3^m-7^n = 2$.
Solusi: Karena $3^6 \equiv 1$ (mod $7$), persamaan yang diberikan menghasilkan $3^m – 2 \equiv 0$ (mod $7$) yang menyiratkan bahwa $m = 6k + 2, k ∈ \mathbb{N}_0$.
Ketika $m = 2$, maka $n = 1$, dan mudah untuk melihat bahwa (2, 1) adalah solusi.
Ketika $m = 2s ≥ 4, s ∈ \mathbb{N}$, maka $27 | (2 + 7^n)$. Karena $7^9 \equiv 1$ (mod $27$) dan $7^4 \equiv -2$ (mod $27$), diperoleh bahwa $n = 9t + 4$. Persamaan yang diberikan menjadi $$9^s=2+7^{9t+4}.$$ Namun, jika kedua sisi diambil modulo $37$, di sisi kanan $7^9 \equiv 1$ (mod $37$) menghasilkan $$2+7^{9t+4}\equiv 2+7^4\equiv 35\text{ }\text{ }\text{ }(\text{mod }37),$$ dan di sisi kiri, sisa $r(s)$ dari $9^s$ modulo $37$ tidak dapat mengambil nilai $35$, karena $9^9 \equiv 1$ (mod $37$), dan untuk $1 ≤s ≤ 9$, kita memiliki tabel
Ini menyiratkan bahwa tidak ada solusi untuk $m ≥ 4$. Jadi, solusi uniknya adalah (2, 1). - Buktikan bahwa terdapat banyak pasangan bilangan bulat positif $(m, n)$ tak terhingga sehingga $$\frac{m+1}{n}+\frac{n+1}{m}$$ adalah bilangan bulat positif.
Solusi: Jelas bahwa jika $n = m$, maka hanya (2, 2) yang merupakan solusi. Untuk $n ≠ m$, kita dapat mengasumsikan bahwa $m < n$. Berdasarkan pengamatan, $m = 1, n = 2$ adalah solusi. Misalkan bahwa $(m, n)$ adalah solusi dan $$\frac{m+1}{n}+\frac{n+1}{m}=k\in\mathbb{N}.$$ Maka $$k=\frac{1}{n}\left[ \frac{n(n+1)}{m}+m+1 \right]\Rightarrow kn=\frac{n(n+1)}{m}+m+1\in\mathbb{N}\Rightarrow \frac{n(n+1)}{m}\in\mathbb{N}.$$ Misalkan $r=\frac{n(n+1)}{m}$, maka $$k=\frac{1}{n}(r+m+1)=\frac{1}{n}\left[ r+\frac{n(n+1)}{r}+1 \right]=\frac{r+1}{n}+\frac{n+1}{r}.$$ Oleh karena itu, $(m, n)$ adalah solusi, menyiratkan bahwa $(n, r)$ juga merupakan solusi baru, karena $r=\frac{n(n + 1)}{m} >n+1> n$. Dengan demikian, jika kita memiliki solusi $(m, n)$ dengan $m < n$, maka harus ada solusi baru $(n, r)$ dengan $n < r$. Dengan melanjutkan proses ini hingga tak terhingga kali, tak terhingga banyaknya solusi berbeda yang dapat diperoleh. - Temukan semua tripel $(p, q, n)$, di mana $p, q$ adalah bilangan prima ganjil dan $n$ adalah bilangan bulat lebih besar dari $1$, yang memenuhi $$q^{n+2}\equiv 3^{n+2}\text{ }(\text{mod }p^n)\text{ dan }p^{n+2}\equiv 3^{n+2}\text{ }(\text{mod }q^n).$$
Solusi: Jelaslah bahwa $(3, 3, n), n = 2, 3, 4,…$ adalah solusi.
Misalkan $(p, q, n)$ adalah solusi lain dengan $p ≠ q, p ≠3, q ≠3$. Kita dapat mengasumsikan bahwa $q > p ≥ 5$.
Jika $n = 2$, maka $q^2 | (p^4 – 3^4)$, yaitu $q^2 | (p^2 – 3^2)(p^2 + 3^2)$. Karena $q$ tidak dapat membagi $(p^2 -3^2)$ dan $(p^2 +3^2)$ secara bersamaan, $q^2$ hanya membagi satu dari $(p^2 – 3^2)$ dan $(p^2 +3^2)$. Namun, $0 < p^2- 3^2 < q^2, p^2 + 3^2 ≠ q^2$ dan $p^2 +3^2 <2p^2 < 2q^2$, sebuah kontradiksi.
Jika $n ≥ 3$, maka $p^n | (q^{n+2} – 3^{n+2})$ dan $q^n | (p^{n+2} – 3^{n+2})$ menghasilkan $$p^n | (p^{n+2} +q^{n+2} -3^{n+2})\text{ dan } q^n | (p^{n+2} +q^{n+2}-3^{n+2}).$$ $(p^n,q^n)=1$ maka menghasilkan $$p^nq^n (p^{n+2}+q^{n+2}-3^{n+2}),\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(22.2)$$ maka $p^nq^n \le p^{n+2} +q^{n+2}-3^{n+2}<2q^{n+2}$, jadi $p^n<2q^2$.
Di sisi lain, $q^n|p^{n+2}-3^{n+2}$ dan $p > 3$ menyiratkan bahwa $q^n\le p^{n+2}-3^{n+2}<p^{n+2}$, jadi $q<p^{1+\frac{2}{n}}$. Menggabungkannya dengan $p^n<2q^2$ menghasilkan $p^n<2p^{2+\frac{4}{n}}<p^{3+\frac{4}{n}}$, oleh karena itu $n < 3+\frac{4}{n}$, yaitu $n = 3$. Jadi, $p^3 | q^5 – 3^5$ dan $q^3 | p^5 – 3^5$.
Karena $5^5 – 3^5 = 2 \times 11 \times 131$ yang tidak mengandung faktor apa pun dalam bentuk $q^3$ untuk beberapa bilangan prima $q$, jadi $p > 5$. $p^3 | (q^5 – 3^5)$ menyiratkan bahwa $p | (q^5 – 3^5)$, dan Teorema Kecil Fermat menghasilkan $p | (q^{p-1} – 3^{p-1})$. Ketika $(5, p — 1) = 1$ dan $p\nmid (q – 3)$, maka $(q^5 – 3^5)/(q – 3), (q^{p−1} — 3^{p−1})/(q − 3) ≥ p > 1$. Namun, misalnya, jika $p – 1 = 5k + 4$, maka $$\left(\frac{q^5-3^5}{q-3},\frac{q^{p-1}-3^{p-1}}{q-3}\right)$$ $$= (q^4+ q^3\cdot 3 + …+ q\cdot 3^3+3^4, q^{p-2} + q^{p-3}\cdot 3+… + q\cdot 3^{p-3}+3^{p-2})$$ $$= (q^4 + q^3\cdot 3+… +3^4,q^{p-2} + q^{p-3}\cdot 3+q^{p-4}\cdot 3^2 +q^{p-5}\cdot 3^3)$$ $$= (q^4 + q^3\cdot 3+…+3^4,q^{p-6}\cdot 3^4) = (q^4 +q^3\cdot 3+…+3^4, q^{p-7}\cdot 3^4)$$ $$= … = (q^4 +q^3\cdot 3+… +3^4, 3^4) =1,$$ dan hasil yang sama juga dapat diperoleh untuk $p – 1 = 5k + r, r = 1,2, 3$.
Jadi, $p | (q -3)$ jika $(5, p – 1) = 1$, yaitu $q\equiv 3$ (mod $p$). Maka $$\frac{q^5-3^5}{q-3}=q^4+3q^3+…+3^4\equiv 5\times 3^4\not\equiv 0\text{ }(\text{mod }p).$$ maka $p^3 |q – 3$. Namun, $q^3 | (p^5 – 3^5)$ memberikan $$q^3\le p^5-3^5<p^5=(p^3)^{\frac{5}{3}}<q^{\frac{5}{3}},$$ kontradiksi. Kontradiksi serupa diperoleh jika $(5, q – 1) = 1.$
Jadi, kita asumsikan bahwa $(5, p – 1) = (5, q – 1) = 5. (q,p-3) = 1$ (karena $q > p ≥ 7$) dan $q^3 | (p^5 – 3^5)$ menyiratkan bahwa $q^3|\frac{p^5-3^5}{p-3}$, maka $$q^3\le \frac{p^5-3^5}{p-3}=p^4+p^3\cdot 3+p^2\cdot 3^2+p\cdot 3^3+3^4.$$ $5|(p-1)$ dan $5|(q-1)$ menyiratkan bahwa $p ≥ 11,q ≥ 31$. Oleh karena itu $$q^3\le p^4\left( 1+\frac{3}{p}+\left( \frac{3}{p} \right)^2 +\left( \frac{3}{p} \right)^3 +\left( \frac{3}{p} \right)^4 \right)<p^4\cdot \left( 1-\frac{3}{4} \right)^{-1}\le \frac{11}{8}p^4.$$ karena $$\left(\frac{q}{p}\right)^3\le \frac{11}{8}p$ dan $\frac{q^2}{p^3}=\left[\left(\frac{q}{p}\right)^3\right]^{\frac{2}{3}}\cdot \frac{1}{p}\le \left(\frac{11}{8}\right)^{\frac{2}{3}}\cdot p^{-\frac{1}{3}}<\frac{5}{8}.$$ Jadi, $$\frac{p^5+q^5-3^5}{p^3q^3}<\frac{p^2}{q^3}+\frac{q^2}{p^3}<\frac{1}{31}+\frac{5}{8}<1.$$ yang bertentangan dengan (22.2). Jadi, solusinya adalah $(3, 3, n), n = 2, 3, 4, ….$
“Inside you lies a strength far greater than you can imagine. Keep pushing yourself to uncover your true abilities.”
