Nilai Absolut dan Aplikasinya
Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Sifat Dasar Nilai Absolut
- Contoh Soal
Untuk setiap bilangan riil $a$, kita mendefinisikan nilai absolutnya, dilambangkan dengan $|a|$, sebagai berikut: $$|a| = \left\{ \begin{array}{cl}
a, & \text{jika }a> 0 \\
0, & \text{jika }a= 0 \\
-a, & \text{jika }a<0.
\end{array} \right.$$ Secara geometris, setiap bilangan riil a dilambangkan dengan sebuah titik pada sumbu bilangan, dan nilai absolut $a$ adalah jarak titik yang mewakili $a$ dari titik asal sumbu bilangan.
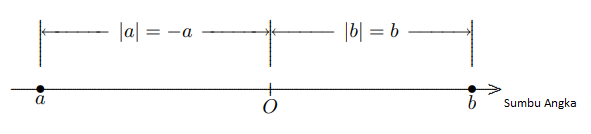
Secara umum, ekspresi $|a − b|$ menunjukkan jarak antara titik-titik pada sumbu bilangan yang mewakili bilangan $a$ dan $b$.
Ketika mengambil nilai absolut untuk setiap ekspresi aljabar, nilai non-negatif selalu dapat diperoleh darinya dengan menghilangkan tanda negatifnya jika nilai ekspresi tersebut adalah “−”. Aturan ini serupa dengan aturan untuk mengkuadratkan ekspresi tersebut.
Sifat Dasar Nilai Absolut
- $|a|=|-a|;$
- $-|a|\le a\le |a|;$
- $|a|=|b|\text{ jika dan hanya jika }a=b\text{ atau }a=-b.$
- $|a^n|=|a^n|\text{ untuk setiap bilangan positif }n;$
- $|ab|=|a|\cdot |b|;$
- $\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\text{ jika }b\neq 0;$
- $|a\pm b|\le |a|+|b|.$
Contoh Soal
- Apakah ada bilangan riil $x$ yang menyebabkan $\frac{|x − |x||}{x}$ merupakan bilangan positif?
Solusi: Sudah jelas bahwa $x\neq 0$.
Untuk $x>0,\frac{|x-|x||}{x}=\frac{|x-x|}{x}=\frac{0}{x}=0.$
Untuk $x<0,\frac{|x-|x||}{x}=\frac{|x-(-x)|}{x}=\frac{|2x|}{x}=\frac{-2x}{x}=-2.$
Jadi, tidak ada bilangan riil $x$ yang menyebabkan pecahan yang diberikan bernilai positif. - Jika $a, b, c$ adalah bilangan riil bukan nol, temukan semua nilai yang mungkin dari ekspresi $\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}.$
Solusi: Karena $\frac{x}{|x|}=1$ untuk setiap $x>0$ dan $\frac{x}{|x|}=-1$ untuk setiap $x<0,$ $$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=-3\text{ jika }a,b,c\text{ semuanya negatif};$$ $$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=-1\text{ jika tepat dua dari }a,b,c\text{ negatif};$$ $$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=1\text{ jika tepat satu dari }a,b,c\text{ negatif};$$ $$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}=3\text{ jika }a,b,c\text{ semuanya positif}.$$ Jadi, nilai yang mungkin dari ekspresi yang diberikan adalah $−3, −1, 1$ dan $3$. - Tentukan syarat persamaan $\left|\frac{a-b}{a}\right|=\frac{b-a}{a}$.
Solusi: Persamaan yang diberikan menyiratkan bahwa $a\neq 0$ dan $\left|\frac{a-b}{a}\right|=-\frac{a-b}{a}$, oleh karena itu $\frac{a-b}{a}\le 0$. Karena $$\frac{a-b}{a}\le 0\Longleftrightarrow 1-\frac{b}{a}\le 0\Longleftrightarrow \frac{b}{a}\ge 1,$$ syarat pada $a$ dan $b$ adalah $\frac{b}{a}\ge 1$. - $a,b,c$ adalah bilangan riil yang memenuhi $(3a+6)^2+|\frac{1}{4}b-10|+|c+3|=0$. Tentukan nilai dari $a^{10}+bc$.
Solusi: Setiap suku pada ruas kiri persamaan yang diberikan adalah non-negatif, kita harus memiliki $$3a+6=0\text{ }\text{ }\frac{b}{4}-10=0\text{ }\text{ }c+3=0$$ pada saat yang sama, oleh karena itu $a = −2, b = 40, c = −3$, sehingga $$a^10+bc=(-2)^{10}+(40)(-3)=1024-120=904.$$ - Diberikan $1 < x < 3$, sederhanakan ekspresi berikut:
(i) $\frac{|x-3|}{x-3}-\frac{|x-1|}{(1-x)}.$
(ii) $|x-1|+|3-x|.$
Solusi: Untuk menyederhanakan ekspresi dengan nilai absolut, perlu mengubahnya menjadi ekspresi normal dengan menghilangkan tanda absolut. Untuk ini, kita perlu mempartisi rentang $x$ menjadi beberapa interval, sehingga pada setiap interval tanda ekspresi tersebut tetap (hanya positif atau hanya negatif). Misalnya, untuk menghilangkan tanda absolut $|x−3|$, perlu mengambil $x−3 = 0$, yaitu $x = 3$ sebagai titik asal, dan tanda $x − 3$ berubah pada titik ini: positif ketika $x > 3$, dan negatif ketika $x < 3$, sehingga perlu membahas $|x − 3|$ untuk $x > 3$ dan $x < 3$ secara terpisah. Dengan demikian, karena rentang $x$ dari kanan ke $1$ dan dari kiri ke $3$,
(i) $x-3<0$ dan $x-1>0$ menyiratkan $|x-3|=-(x-3),|x-1|=x-1,$ maka, $$\frac{|x-3|}{x-3}-\frac{|x-1|}{(1-x)}=\frac{-(x-3)}{x-3}-\frac{x-1}{1-x}=-1-(-1)=0.$$
(ii) Dengan alasan yang sama, $|x-1|+|3-x|=(x-1)+(3-x)=2.$ - Diketahui $1<x<3$, sederhanakan $|x-2|+2|x|$.
Solusi: Titik nol dari $|x−2|$ dan $|x|$ masing-masing adalah $x = 2$ dan $x = 0$. Perlu untuk membagi rentang $x$ menjadi dua interval: $1 < x ≤ 2$ dan $2 < x <3$.
(i) Ketika $1<x\le 2,\text{ }|x-2|+2|x|=2-x+2x=2+x;$
(ii) Ketika $2<x<3,\text{ }|x-2|+2|x|=x-2+2x=3x-2.$ - Sederhanakan $||x+2|-7|-|7-|x-5||$ untuk $-2<x<5.$
Solusi: Kita hilangkan tanda absolut dari lapisan dalam ke lapisan luar. Karena $x + 2 > 0$ dan $x − 5 < 0$, $$||x+2|-7|-|7-|x-5||=|(x+2)-7|-|7-(5-x)|$$ $$=|x-5|-|2+x|=(5-x)-(2+x)=3-2x$$ - Tentukan jumlah solusi nyata dari persamaan $|x − 2| + |x − 3| = 1$.
(A) 0, (B) 1, (C) 2, (D) 3, (E) lebih dari 3.
Solusi: Kita perlu membahas Tiga kasus: $x\le 2;2<x\le 3$, dan $3<x$.
(i) Ketika $x\le 2,$ $$|x-2|+|x-3|=1\Leftrightarrow (2-x)+(3-x)=1\Leftrightarrow x=2;$$
(ii) Ketika $2<x\le 3,$ $$|x-2|+|x-3|=1\Leftrightarrow (x-2)+(3-x)=1\Leftrightarrow \text{ setiap }x\in (2,3]\text{ adalah solusi}.$$
Maka jawabannya adalah (E). - Misalkan posisi titik-titik pada sumbu bilangan yang mewakili bilangan riil $a, b, c$ seperti yang ditunjukkan pada diagram berikut. Tentukan nilai persamaan tersebut. $$|b-a|+|a-c|+|c-b|.$$
Solusi: Dari diagram kita menemukan bahwa $c < b < 0 < a < −c$, oleh karena itu $$|b-a|+|a-c|+|c-b|=(a-b)-(a-c)+b-c=0.$$ Jadi, nilai dari ekspresi tersebut adalah 0. - Diberikan $m=|x+2|+|x-1|-|2x-4|$. Tentukan nilai maksimum dari $m$.
Solusi: Kami membahas nilai maksimum $m$ pada masing-masing tiga
(i) Ketika $x\le -2$, maka $$m=-(x+2)-(x-1)+(2x-4)=-5.$$
(ii) Ketika $-2<x\le 1$, maka $$m=(x+2)-(x-1)+(2x-4)=2x-1\le 1.$$
(iii) Ketika $1<x\le 2$, maka $$m=(x+2)+(x-1)+(2x-4)=4x-3\le 5$$
(iv) Ketika $2<x$, maka $$m=(x+2)+(x-1)+(4-2x)=5.$$
Jadi, $m_{max}=5$. - Misalkan $a<b<c$, Tentukan nilai minimum dari ekpresi berikut $$y=|x-a|+|x-b|+|x-c|.$$
Solusi:
(i) Ketika $x\le a$, $$y=(a-x)+(b-x)+(c-x)\ge (b-a)+(c-a)$$
(ii) Ketika $a<x\le b$, $$y=(x-a)+(b-x)+(c-x)=(b-a)+(c-x)\ge (b-a)+(c-b)=c-a$$
(iii) Ketika $b<x\le c$, $$y=(x-a)+(x-b)+(c-x)=(x-a)+(c-b)>(b-a)+(c-b)=c-a$$
(iv) Ketika $c<x$, $$y=(x-a)+(x-b)+(x-c)>(b-a)+(c-b)+(x-c)>c-a$$
Jadi, $y_{min}=c-a$, dan $y$ mencapai nilai minimum ini pada $x=b$.
“If you are working on something that you really care about, you don’t have to be pushed. The vision pulls you.”
