Kekongruensian Segitiga

Pengantar Pemecahan Masalah

Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit

Kelas

Materi ini ditunjukan untuk siswa berbakat kelas 4, 5, 6, 7 dan 8

Presentasi

Unduh

Video Pengantar

fira

Video Lanjutan

Pre Test

Post Test

Referensi Tambahan

Unduh

Dua segitiga disebut kongruen jika dan hanya jika bentuk dan ukurannya sama.

Dalam geometri, kongruensi segitiga merupakan alat yang sangat penting dan mendasar dalam membuktikan hubungan kesetaraan atau ketidaksetaraan dua elemen geometri (misalnya, dua ruas garis, dua sudut, dua jumlah sisi, dua selisih sudut, dll.). Dua segitiga kongruen berarti keduanya sama dalam semua aspek, sehingga setiap elemen geometri yang bersesuaian juga sama.

Untuk membuktikan dua elemen geometri sama, akan lebih mudah jika kita membangun dua segitiga kongruen sedemikian rupa sehingga kedua elemen tersebut merupakan elemen-elemen yang bersesuaian dari segitiga kongruen tersebut.

Untuk membuktikan dua elemen geometri sama atau tidak sama, meskipun posisi mereka berjauhan, dengan menggunakan kongruensi dua segitiga, kita dapat menggeser posisi segitiga yang memuat satu elemen, sehingga kedua elemen tersebut diposisikan bersama sehingga perbandingannya menjadi jauh lebih mudah.

Kriteria Dasar Kekongruensian Dua Segitiga

S.A.S. : Dua sisi dan sudut yang termasuk di dalamnya pada satu segitiga sama besar dengan sisi dan sudut yang termasuk di dalamnya pada segitiga lainnya.
A.A.S. : Dua sudut dan satu sisi suatu segitiga sama besar dengan sisi-sisi pada segitiga lainnya.
S.S.S. : Tiga sisi suatu segitiga sama panjang dengan sisi segitiga lainnya secara berurutan.
Untuk segitiga siku-siku, kriteria ini dapat disederhanakan sebagai berikut:
S.A. : Satu sisi dan satu sudut lancip suatu segitiga sama besar dengan sisi segitiga lainnya.
S.S. : Dua sisi suatu segitiga sama panjang dengan sisi segitiga lainnya.

Contoh Soal

Seperti yang ditunjukkan pada diagram, jika pada $\Delta ABC, AB = AC$, $D$ berada pada $AB$ dan $E$ berada pada perpanjangan $AC$ sehingga $BD = CE$. Ruas garis $DE$ berpotongan dengan $BC$ di titik $G$. Buktikan bahwa $DG = GE$.

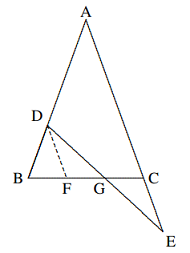
Solusi: Dari $D$, masukkan $DF || AE$, yang berpotongan dengan $BC$ di $F$, seperti yang ditunjukkan pada diagram samping. Kemudian $$∠FDG = ∠CEG, ∠DGF = ∠EGC.$$ Karena $∠BFD = ∠BCA = ∠DBF$, kita punya $$DF=DB=CE.$$ Oleh karena itu, $$\Delta DFG \cong \Delta ECG(\text{A.A.S.}),$$ Maka $DG=GE$.
Diketahui $BE$ dan $CF$ adalah garis tinggi dari $\Delta ABC$. $P, Q$ masing-masing berada pada $BE$ dan perpanjangan $CF$ sehingga $BP = AC, CQ = AB$. Buktikan bahwa $AP ⊥ AQ$.
Solusi: Dari $AB\bot CQ$ dan $BE\bot AC$ $$∠ABE = ∠QCA.$$ Maka $AB=CQ$ dan $BP=CA$, $$\Delta ABP\cong \Delta QCA\text{ (S.A.S.)},$$ $$∴ ∠BAP = ∠CQA,$$ $$∴ ∠QAP = ∠QAF + ∠BAP$$ $$= ∠QAF + ∠CQA$$ $$= 180◦ − 90◦ = 90◦.$$
Pada bangun sama sisi $\Delta ABC$, titik $D$ dan $E$ masing-masing berada di $AC$ dan $AB$, sehingga $BD$ dan $CE$ berpotongan di titik $P$, dan luas segiempat $ADPE$ sama dengan luas $\Delta BPC$. Tentukan $∠BPE$.

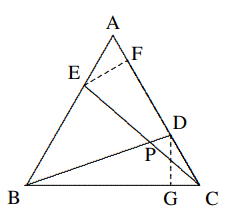
Solusi: Dari $E$ dan $D$ masukkan $EF ⊥ AC$ pada $F$ dan $DG ⊥ BC$ pada $G$.
Kondisi $[ADPE] = [BPC]$ menyiratkan bahwa $$[ACE] = [CBD]. $$ Karena $AC = BC$, maka $EF = DG$. Karena $∠A =∠C$, maka Rt$\Delta AEF \cong$ Rt$\Delta CDG \text{ (A.S.)}$. Oleh karena itu, $AE = CD$, sehingga $$\Delta AEC\cong\Delta CDB\text{ (S.A.S.)}$$ Karena, $\angle DBC=\angle ECD$, sehingga $$∠BPE = ∠PBC + ∠PCB = ∠PCD + ∠PCB = 60◦.$$
Diketahui $ABC$ adalah segitiga sama sisi dengan sisi $1$, $\Delta BDC$ adalah segitiga sama kaki dengan $DB = DC$ dan $∠BDC = 120◦$. Jika titik $M$ dan $N$ berada pada $AB$ dan $AC$ sehingga $∠MDN = 60◦$, tentukan keliling $\Delta AMN$.

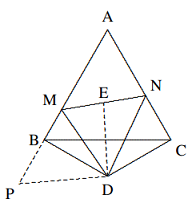
Solusi: $∵ ∠DBC = ∠DCB = 30◦, ∴ DC ⊥ AC, DB ⊥ AB.$
Dengan memperluas $AB$ ke $P$ sehingga $BP = NC$, maka $\Delta DCN \cong \Delta DBP \text{ (S.S.)}$, maka $DP =DN$. $∠PDM = 60◦ = ∠MDN$ menyiratkan bahwa $$\Delta PDM \cong \Delta MDN,\text{ (S.A.S.)},$$ $$∴ PM = MN,$$ $$∴ MN = PM = BM + PM = BM + NC.$$ Jadi, keliling $\Delta AMN$ adalah $2$.
Catatan: Di sini kongruensi $\Delta PDM \cong \Delta MDN$ diperoleh dengan memutar $\Delta DCN$ ke posisi $\Delta DBP$ pada dasarnya.
Seperti yang ditunjukkan pada gambar, pada $\Delta ABC$, $D$ adalah titik tengah $BC$, $∠EDF = 90◦$, $DE$ memotong $AB$ di $E$ dan $DF$ memotong $AC$ di $F$. Buktikan bahwa $$BE+CF>EF$$

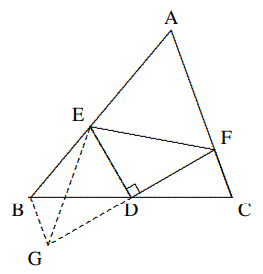
Solusi: Dalam soal ini, untuk membandingkan $BE + CF$ dan $EF$, diperlukan untuk memindahkan segmen $BE, EF, CF$ bersama-sama dalam segitiga yang sama, dan membangun segitiga kongruen dapat menyelesaikan tugas ini sebagai berikut.
Putar $\Delta DCF$ di sekitar $D$ sebesar $180◦$ searah jarum jam, maka $$C\to B,\text{ }\text{ }\text{ }F\to G.$$ Hubungkan $BG, EG, GD$. Karena $BG = CF$ dan $GD = DF$, kita peroleh $$\Delta EDG\cong \Delta EDF,\text{ (S.S.)},$$ maka $$EF = EG < BE + BG = BE + CF.$$
Diketahui $\Delta ABC$ adalah segitiga siku-siku sama kaki dengan $∠ACB = 90◦$. $D$ adalah titik tengah $BC, CE$ tegak lurus terhadap $AD$, berpotongan dengan $AB$ dan $AD$ di $E$ dan $F$ berturut-turut. Buktikan bahwa $∠CDF = ∠BDE$.

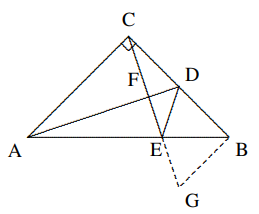
Solusi: Tidak praktis untuk membandingkan $∠CDF$ dan $∠BDE$ secara langsung. Untuk mengubah
posisi $∠CDF$, misalkan garis tegak lurus dari $B$ ke $BC$ berpotongan dengan garis $CE$ di $G$. Karena $AC = CB$, $$∠CAD = ∠BCG = 90◦ − ∠ACF,$$ $$\Delta ACD \cong \Delta CBG \text{ (S.A.)},$$ $$∴ ∠CDF = ∠BGC = ∠BGE.$$ $$∵ BD = CD = BG\text{ dan } ∠DBE = ∠GBE = 45◦,$$ $∴ \Delta BGE \cong \Delta BDE (S.A.S.), \text{ maka }∴ ∠CDF = ∠BGE = ∠BDE.$
Pada persegi $ABCD$, $E$ adalah titik tengah $AD, BD$, dan $CE$ berpotongan di $F$. Buktikan bahwa $AF ⊥ BE$.

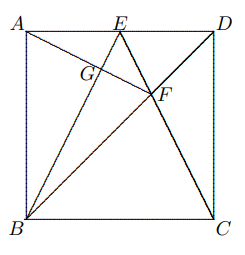
Solusi: Misalkan $G$ adalah titik potong $AF$ dan $BE$. Cukup ditunjukkan $$∠EAG = ∠ABG.$$ Berdasarkan simetri yang kita miliki $$\Delta ABE \cong \Delta DCE, \Delta ADF \cong \Delta CDF,$$ oleh karena itu $∠EAG = ∠DCF = ∠ABG.$
Pada grafik, segitiga $ABD$ dan $BEC$ keduanya sama sisi dengan $a, b$, dan $c$ kolinear, $M$ dan $N$ masing-masing adalah titik tengah $AE$ dan $CD, AE$ berpotongan dengan $BD$ di $G$ dan $CD$ berpotongan dengan $BE$ di $H$. Buktikan bahwa (i) $\Delta MBN$ sama sisi, (ii) $GH || AC$.

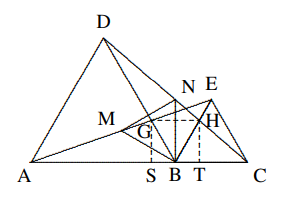
Solusi: (i) Dari $AB = BD, BE = BC, ∠ABE = ∠DBC = 120◦$ $$\Delta ABE \cong \Delta DBC \text{ (S.A.S.)},$$ $$∴ ∠MAB = ∠NDB, MA = ND,$$ yang berarti $\Delta MAB\cong \Delta NDB \text{ (S.A.S.)}.$ $$∴ MB = NB \text{ dan } ∠ABM = ∠DBN$$ $$∠MBN = ∠MBD + ∠ABM = ∠ABD$$ $$= 60◦, \Longrightarrow \Delta MBN\text{ sama sisi}.$$
(ii) Dari $G, H$ memperkenalkan $GS ⊥ AC$ di $S$ dan $HT ⊥ AC$ di $T$ masing-masing. Karena $$∠GBA = ∠ECA = ∠HBC = ∠DAC = 60◦ \Longrightarrow GB || CE, HB || AD,$$ $$\Longrightarrow GB=\frac{AB}{AC}\cdot CE,HB=\frac{BC}{AC}\cdot AD\Longrightarrow GB=HB.$$ Karena $∠GBS = ∠HBT = 60◦$, jadi Rt$\Delta GBS\cong$ Rt$\Delta HBT\text{(S.A.)}$. Maka, $GS=HT,$ yaitu $GH||AC$.

Solusi dari setiap Permasalahan diberikan pada kelas online

“Coming together is a beginning. Keeping together is progress. Working together is success.”