Fungsi Trigonometri

Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Definisi
- Sifat Dasar Fungsi Trigonometri
- Contoh Soal
Definisi
Definisi 1. Fungsi Trigonometri Untuk Sudut Lancip
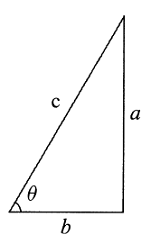
$$\begin{array}{rcl}
\sin \theta=\frac{a}{c}; & \cos \theta =\frac{b}{c}; \\
\tan \theta =\frac{a}{b}; & \cot \theta =\frac{b}{a}; \\
\sec \theta=\frac{c}{b}; & \csc \theta =\frac{c}{a}.
\end{array}$$
Definisi 2. Fungsi Trigonometri untuk Semua Sudut
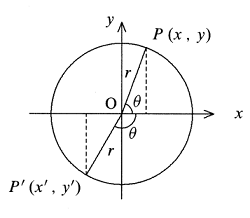
$$\begin{array}{rcl}
\sin \theta=\frac{y}{r}; & \cos \theta =\frac{x}{r}; \\
\tan \theta =\frac{y}{x}; & \cot \theta =\frac{x}{y}; \\
\sec \theta=\frac{r}{x}; & \csc \theta =\frac{r}{y}.
\end{array}$$- Sudut positif dan negatif: Sudut yang diukur dari sumbu $x$ berlawanan arah jarum jam adalah sudut positif. Sudut yang diukur dari sumbu $x$ searah jarum jam adalah sudut negatif.
- Tanda-tanda fungsi trigonometri pada setiap kuadran berbeda adalah

- Keenam fungsi tersebut masing-masing periodik dengan periode umum $2π$ (atau $360°$). Baik $\sin x$ maupun $\cos x$ memiliki rentang $[-1, 1]$, baik $\tan x$ maupun $\cot x$ memiliki rentang $(-\infty , +\infty )$, dan baik $| \sec x|$ maupun $| \csc x|$ tidak boleh kurang dari $1$.
Fungsi $\sin x,\tan x,\csc x$ adalah fungsi ganjil, dan $\cos x, \cot x, \sec x$ adalah fungsi genap.
Sifat Dasar Fungsi Trigonometri
- Grafik $y = \sin x, y = \cos x, y = \tan x, y = \cot x$ digambarkan sebagai berikut:
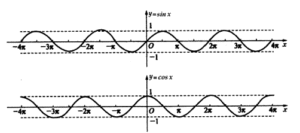
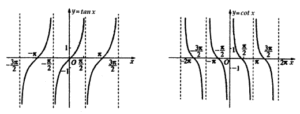
- Masing-masing dari keenam fungsi tersebut merupakan fungsi periodik. $y = \sin x$ dan $y = \cos x$ mengambil $2\pi$ sebagai periode minimumnya; dan masing-masing memiliki rentang $[-1, 1]$. $y = \tan x$ dan $y = \cot x$ diambil $\pi$ sebagai periode minimumnya, dan masing-masing memiliki rentang $(-∞, +∞)$.
- $y = \sin x, x \in \mathbb{R}$ adalah fungsi ganjil, dan meningkat pada $[-\frac{\pi}{2},\frac{\pi}{2}]$, dengan
rentang $[-1, 1]$.
$y = \cos x, x \in \mathbb{R}$ adalah fungsi genap, dan menurun pada $[0, π]$, dengan rentang $[-1, 1]$.
$y = \tan x$ adalah fungsi ganjil, dan meningkat pada $(-\frac{\pi}{2},\frac{\pi}{2})$, dengan rentang $(-\infty , +\infty )$.
$y = \cot x$ adalah fungsi ganjil, dan menurun pada $(, \pi)$, dengan rentang $(-\infty , +\infty )$. - Fungsi $y = \sin{-1}x$ meningkat, memiliki domain $[-1, 1]$ dan rentang $[-, -\frac{\pi}{2},\frac{\pi}{2}]$.
Fungsi $y = cos^{-1} x$ menurun, memiliki domain $[-1, 1]$ dan rentang $[0, π]$.
Fungsi $y = tan^{-1} x$ meningkat, memiliki domain $(-\infty , +\infty )$ dan rentang $(-\frac{\pi}{2},\frac{\pi}{2})$.
Fungsi $y = cot^{-1} x$ menurun, memiliki domain $(-\infty , +\infty )$ dan rentang $(0, \pi)$.
Berikut sketsa mereka, dalam urutan tersebut: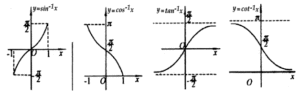
Contoh Soal
- Untuk $\alpha \in (0,\frac{\pi}{4})$, susun $(\sin \alpha)^{\cos \alpha},(\cos \alpha )^{\sin \alpha},(\sin \alpha)^{\sin \alpha}$ dalam urutan menurun.
Solusi: Karena $0<\sin \alpha <\cos \alpha <1$ untuk $0<\alpha <\frac{\pi}{4}$. $$(\cos \alpha)^{\sin \alpha}>(\sin \alpha)^{\sin \alpha}\text{ dan }(\sin \alpha)^{\sin \alpha}>(\sin \alpha)^{\cos \alpha},$$ oleh karena itu $$(\cos \alpha)^{\sin \alpha}>(\sin \alpha)^{\sin \alpha}>(\sin \alpha)^{\cos \alpha}.$$ - Bandingkan nilai $\cos(\cos x)$ dan $\sin(\sin x)$, jika $0\le x\le \pi$.
Solusi: Pertama-tama, $\pi>\frac{\pi}{2}-\cos x>\frac{\pi}{2}-1>0$ dan $$\frac{\pi}{2}-\cos x-\sin x=\frac{\pi}{2}-\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)\ge \frac{\pi}{2}-\sqrt{2}>0.$$
(i) Ketika $0\le x\le \frac{\pi}{2}$, sudut $\alpha_1=\frac{\pi}{2}-\cos x,\alpha_2=\sin x$ keduanya dalam $[0,\frac{\pi}{2}]$. Karena $\sin u$ adalah meningkat pada $[0,\frac{\pi}{2}]$, maka $$\cos(\cos x)-\sin(\sin x)=\sin \left(\frac{\pi}{2}-\cos x\right)-\sin(\sin x)=\sin \alpha_1-\sin \alpha_1-\sin \alpha_2>0.$$
(ii) Ketika $\frac{\pi}{2}<x\le \pi$, $$\frac{\pi}{2}\le \alpha_1=\frac{\pi}{2}-\cos x,\text{ }0\le\alpha_2=\sin x\le 1$$ dan $$\alpha_1+\alpha_2=\frac{\pi}{2}-\cos x+\sin x\le \frac{\pi}{2}+\sqrt{2}<\pi,$$ maka $\frac{\pi}{2}\le \alpha_1<\pi-\alpha_2$. Jadi $$\cos(\cos x)=\sin(\alpha_1)>\sin(\pi-\alpha_2)=\sin \alpha_2=\sin(\sin x).$$ Jadi, $\cos(\cos x)>\sin(\sin x)$ untuk $x \in [0,\pi]$. - Pada fungsi berikut, fungsi genap dengan $\frac{\pi}{2}$ sebagai periode minimumnya adalah
(A) $y = \sin 2x + \cos 2x;$ (B) $y = \sin 2x \cos 2x;$
(C) $y = \sin^2 x + \cos 2x;$ (D) $y = \sin^2 2x – \cos^2 2x.$
Solusi: Pada (A) ambil $x =\frac{\pi}{4}$ maka $y = 1$, dan ambil $x = -\frac{\pi}{4}$ maka $y = -1$, jadi $y$ bukan fungsi genap.
Fungsi pada (B) adalah $y = \frac{1}{2}\sin 4x$, jadi bukan fungsi genap.
Fungsi pada (C) adalah $y =\frac{1+\cos 2x}{2}$, sehingga periode minimumnya adalah $\pi$.
Fungsi pada (D) adalah $y = – \cos 4x$, jadi memenuhi persyaratan. - Tentukanlah range dari fungsi $f(x) = \sin^4 x \cdot \tan x +\cos^4 x\cdot \cot x.$
Solusi: Karena $f(x)=\frac{\sin^5 x}{\cos x}+\frac{\cos^5}{\sin x}=\frac{\sin^6x+\cos^6x}{\sin x\cos x}=\frac{2-\frac{3}{2}\sin^2 2x}{\sin 2x},$ jika misalkan $t=\sin 2x$, maka $t\in [-1,0)\cup (0,1]$ dan $$f(x)=g(t)=\frac{2-\frac{3}{2}t^2}{t}=\frac{2}{t}-\frac{3}{2}t.$$ Karena $2/t$ dan $-\frac{3t}{2}$ keduanya menurun pada $[-1,0)$ dan $(0,1]$, maka $g(t)=\frac{2}{t}-\frac{3}{2}t$ adalah menurun pada $[-1,0)\cup(0,1]$, oleh karena itu rentang $g(t)$ adalah $(-\infty ,-\frac{1}{2}]\cup[\frac{1}{2},+\infty )$.
Jadi, rentang $f(x)$ adalah $\left(-\infty ,-\frac{1}{2}\right]\cup \left[\frac{1}{2},+\infty \right)$. - Buktikan bahwa fungsi $f(x) = \cos x^3,x \in \mathbb{R}$ tidak periodik.
Solusi: Demi kontradiksi, misalkan $T$ adalah periode $f$. Maka $$f(T)=f(0)=1=f(\sqrt[3]{2k\pi})=f(\sqrt[3]{2k\pi}+T),\text{ }k\in \mathbb{Z}.$$ Oleh karena itu, terdapat bilangan bulat $m$ sehingga $T^3 = 2m\pi$ atau $T = \sqrt[3]{2m\pi}$, di mana $m ≠ 0$. Demikian pula, untuk $k = 2m$, terdapat $n ∈ \mathbb{Z}$ sehingga $$(\sqrt[3]{4m\pi}+T)^3=2n\pi,$$ Maka, $$(\sqrt[3]{4m\pi}+\sqrt[3]{2m\pi})^3=2n\pi\Rightarrow 2m\pi(\sqrt[3]{2}+1)^3=2n\pi$$ $$\Rightarrow m(2+3\sqrt[3]{4}+3\sqrt[3]{2}+1)=n\Rightarrow \sqrt[3]{4}+\sqrt[3]{2}=\frac{n}{3m}-1\Rightarrow \sqrt[3]{4}+\sqrt[3]{2}\in \mathbb{Q}.$$ Misalkan $a=\sqrt[3]{2}$, maka $a^2+a\in \mathbb{Q}$. Karena $a^3=2\in \mathbb{Q}$, jadi $a^3-1=1\in \mathbb{Q}$. Maka $$a-1=\frac{a^3-1}{a^2+a+1}\in \mathbb{Q}\Rightarrow a\in \mathbb{Q},$$ yang tidak mungkin: Mudah untuk menunjukkan bahwa $\sqrt[3]{2} \in \mathbb{Q}^o$ dengan kontradiksi. Dengan demikian, kontradiksi tersebut membuktikan kesimpulan bahwa $T$ tidak ada. - Untuk $\theta \in [0,\pi]$ didefinisikan $f(\theta)=\sin(\cos \theta),g(\theta)=\cos(\sin \theta)$. Jika $a=\underset{0\le \theta\le \pi}{\max}$ $f(x),b=\underset{0\le \theta\le \pi}{\min}$ $f(\theta),c=\underset{0\le \theta\le \pi}{\max}$ $g(\theta)$, dan $d=\underset{0\le \theta\le \pi}{\min}$ $g(\theta)$, maka mana yang hubungan ini benar?
(A) $b<d<a<c;$ (B) $d<b<c<a;$ (C) $b<d<c<a;$ (D) $d<b<a<c.$
Solusi: Pada $[0,\pi]$ fungsi $y_1=\cos \theta$ menurun, dan pada $[-1,1]$ fungsi $\sin y_1$ menaik, maka $a=\sin 1,b=\sin (-1)=-\sin 1$.
Pada $[0,\pi]$ fungsi $y_2=\sin \theta$ memiliki rentang $[0,1]$, dan fungsi $\cos y_2$ adalah menurun pada $[0,1]$, maka $c=\cos 0=1,d=\cos 1$.
Lebih lanjut, $1>\frac{\pi}{4}$ menyiratkan bahwa $a=\sin 1>\cos 1=d$.
Maka, $b<d<a<c$, jawaban nya adalah (A). - Diketahui fungsi $f(x)=\frac{6\sin^4x-7\sin^2x+2}{\cos 2x}$. (i) Tentukan domain dan range dari $f$; (ii) Tentukan jika $f$ adalah fungsi ganjil atau fungsi genap.
Solusi:
(i) $\frac{6\sin^4x-7\sin^2x+2}{cos 2x}=\frac{(3\sin^2x-2)(2\sin^2x-1)}{cos 2x}$
$=2-3\sin^2x=3\cos^2x-1=\frac{3}{2}\cos2x+\frac{1}{2}.$
Karena $\cos 2x\neq 0$, maka $2x\neq k\pi+\frac{\pi}{2}$, yaitu domain $f$ adalah $\left\{x:x\neq \frac{k\pi}{2}+\frac{\pi}{4}\right\}$.
Range $f$ adalah $\left[-1,\frac{1}{2})\cup(\frac{1}{2},2\right]$.
(ii) Karena $\cos 2x$ adalah fungsi genap, begitu juga $f$. - Diketahui $f(x)=\cos 2x-2a(1+\cos x)$ memiliki nilai minimum $-\frac{1}{2}$, tentukan nilai $a$.
Solusi: $f(x)=2\cos^2x-1-2a-2a\cos x=2\left(\cos x-\frac{a}{2}\right)^2-\frac{1}{2}a^2-2a-1.$
(1) Ketika $a>2$, nilai minimum $f$ adalah $1-4a<-7$, dan nilai tersebut diperoleh ketika $\cos x=1$.
(2) Ketika $a<-2$, nilai minimum $f$ adalah $1$, dan nilai tersebut diperoleh ketika $\cos x=-1$.
(3) Ketika $-2\le a\le 2$, nilai minimum $f$ adalah $-\frac{1}{2}a^2-2a-1$, dan nilai tersebut diperoleh ketika $\cos x=\frac{a}{2}$.
Dengan menyelesaikan $-\frac{1}{2}a^2-2a-1=-\frac{1}{2}$, maka diperoleh $a^2+4a+1=0$, jadi $$a=-2+\sqrt{3}\text{ atau }a=-2-\sqrt{3}$$ Karena $|a|\le 2$, maka $a=-2+\sqrt{3}$.
Solusi dari setiap Permasalahan diberikan pada kelas online
“We cannot solve our problems with the same thinking we used when we created them.”

