Beberapa Teorema Penting dalam Geometri

- Contoh Soal
Teorema I. (Teorema Nenelaus) Jika suatu garis lurus memotong sisi $AB, BC$ dan $CA$ (atau perpanjangannya) dari suatu $\Delta ABC$ masing-masing di titik $X, Y$ dan $Z$, maka $$\frac{AX}{XB}\cdot \frac{BY}{YC}\cdot \frac{CZ}{ZA}=1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(14.1)$$ (Teorema Menelaus Invers) Untuk sembarang $\Delta ABC$ yang diberikan, jika $X,Y,Z$ adalah titik-titik pada garis $AB,BC,CA$ berturut-turut (di mana tepat satu titik berada pada perpanjangan satu sisi, atau tiga titik semuanya berada pada perpanjangan sisi) sedemikian hingga (14.1) berlaku, maka $X,Y,Z$ pastilah kolinear.
Teorema II. (Teorema Ceva) Untuk setiap segitiga $ABC$ yang diberikan, misalkan $X,Y,Z$ menjadi titik dengan (i) semua pada segmen garis $BC,CA,AB$: atau (ii) tepat satu di satu sisi dan dua lainnya di perpanjangan kedua sisi tersebut. Maka garis $AX,BY,CZ$ sejajar atau konkuren jika dan hanya jika $$\frac{BX}{XC}\cdot \frac{CY}{YA}\cdot \frac{AZ}{ZB}=1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(14.2)$$ Bentuk Trigonometri Teorema Ceva Kondisi (14.2) dapat dinyatakan kembali sebagai $$\frac{\sin\angle BAX\cdot \sin \angle CBY\cdot\sin\angle ACZ}{\sin \angle CAX\cdot \sin\angle ABY\cdot\sin\angle BCZ}=1.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(14.3)$$
Teorema III. (Teorema Simson) Untuk $\Delta ABC$ dan titik $D$ yang berada di luar segitiga, buat tiga garis tegak lurus dari $D$ ke sisi $BC, CA$, yang berpotongan masing-masing di $A_1, B_1, C_1$. Maka, $A_1, B_1$, dan $C_1$ kolinear jika dan hanya jika $A, B, C, D$ konsiklik.
Catatan: Ketika $A_1,B_1,C_1$ kolinear, garis yang melalui nya di sebut Garis Simson.
Teorema IV. (Teorema Ptolemeus) Misalkan $ABCD$ merupakan segiempat cembung. Maka $$AB\cdot CD+AD\cdot BC=AC\cdot BD\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(14.4)$$ jika dan hanya jika $A,B,C,D$ konsiklik.
Teorema Ptolemeus yang Diperluas Untuk setiap segiempat cembung $ABCD$, ketidaksamaan $$AB\cdot CD+AD\cdot BC\ge AC\cdot BD\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(14.5)$$ selalu berlaku, dan persamaan berlaku jika dan hanya jika $A,B,C,D$ konsiklik.
Catatan: (14.5) disebut Ketidaksamaan Ptolemeus.
Contoh Soal
- Untuk dua segitiga $ABC$ dan $A_1B_1C_1$ pada bidang yang sama, bila garis $AA_1,BB_1,CC_1$ berpotongan di titik $S$, maka ketiga titik $P,Q,R$ haruslah kolinear, di mana garis $BC$ dan $B_1C_1$ berpotongan di $P$, garis $CA$ dan $C_1A_1$ berpotongan di $Q$, dan garis $AB$ dan $A_1B_1$ berpotongan di $R$, seperti yang ditunjukkan pada diagram.
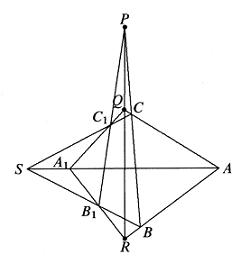
Solusi: Perhatikan garis $PC_1B_1$ sebagai garis transversal terhadap $\Delta SBC$, berdasarkan teorema Menelaus, $$\frac{BP}{PC}\cdot\frac{CC_1}{C_1S}\cdot\frac{SB_1}{B_1B}=1.$$ Karena $QC_1A_1$ melintang ke $\Delta SCA$, maka $$\frac{CQ}{QA}\cdot\frac{AA_1}{A_1S}\cdot\frac{SC_1}{C_1C}=1.$$ Demikian pula, mengingat $RB_1A_1$ melintang ke $\Delta SAB$, maka $$\frac{AR}{RB}\cdot\frac{BB_1}{B_1S}\cdot\frac{SA_1}{A_1A}=1.$$ Mengalikan ketiga persamaan tersebut menghasilkan $$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1.$$ Karena $P,Q,R$ semuanya berada pada ekstensi $BC,CA,AB$, maka $P,Q,R$ pasti kolinear dengan teorema Meneleus invers. - Lingkaran dalam $☉I$ dari $\Delta ABC$ menyinggung sisi-sisi $BC, CA, AB$ masing-masing di $A_1, B_1, C_1$. Misalkan $l$ adalah garis yang melalui $I$ dan $A’,B’,C’$ masing-masing adalah titik-titik simetris $A_1,B_1,C_1$ terhadap $l$. Buktikan bahwa garis-garis $AA’,BB’,CC’$ konkuren.
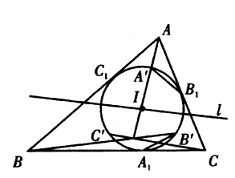
Solusi: Gunakan $d_a(X),d_b(X),d_c(X)$ untuk menyatakan jarak titik $X$ dari garis $BC,CA,AB$. Teorema Ceva dalam bentuk trigonometri memberikan $$AA’,BB’,CC’\text{ kolinear }\Leftrightarrow \frac{\sin\angle CAA’}{\sin\angle BAA’}\cdot \frac{\sin\angle ABB’}{\sin\angle CBB’}\cdot \frac{\sin\angle BCC’}{\sin \angle ACC’}=1$$ $$\Leftrightarrow \frac{d_b(A’)/AA’}{d_c(A’)/AA’}\cdot \frac{d_c(B’)/BB’}{d_a(B’)/BB’}\cdot \frac{d_a(C’)/CC’}{d_b(C’)/CC’}=1$$ $$\Leftrightarrow \frac{d_b(A’)}{d_c(A’)}\cdot \frac{d_c(B’)}{d_a(B’)}\cdot \frac{d_a(C’)}{d_b(C’)}=1.$$ Karena $A’B_1=A_1B’$ dan $CB,CA$ keduanya bersinggungan dengan $☉I$, maka dalam derajat, $$\angle B’A_1C=\frac{1}{2}\widehat{B’A_1}=\frac{1}{2}\widehat{A’B_1}=\angle A’B_1A,$$ $$\Rightarrow d_a(B’)=A_1B’\sin \angle B’A_1C=B_1A’\sin\angle A’B_1A=d_b(A’).$$ Demikian pula, $d_b(C’)=d_c(B’)$ dan $d_c(A’)=d_a(C’)$, kesimpulannya terbukti. - Misalkan $P$ adalah sebuah titik pada lingkaran luar $\Delta ABC$. Dari titik $P$, buatlah tiga garis yang memotong garis $BC, CA, AB$ masing-masing di $D, E, F,$ sehingga $\angle PDB=\angle PEC=\angle PFB$. Maka $D, E, F$ kolinear.
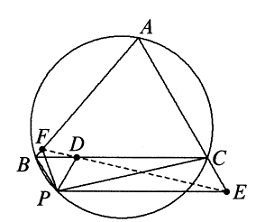
Solusi: Cukup menunjukkan bahwa $\angle PDF+\angle PDE=180^o$. Karena $\angle PDB=\angle PFB$ menyiratkan bahwa $BPDF$ siklik, maka $$\angle PDF+\angle PBF=180^o.$$ $ABPC$ siklik menyiratkan $$\angle PBF=\angle PCE,$$ dan $\angle PDE=\angle PCE$ menyiratkan $PDCE$ siklik, maka $$\angle PDE=\angle PCE=\angle PBF,$$ maka, $\angle PDF+\angle PDE=\angle PDF+\angle PBF=180^o$, maka $D,E,F$ kolinear. - Misalkan $AXYZB$ adalah pentagon cembung yang tertulis dalam setengah lingkaran berdiameter $AB$. Nyatakan dengan $P,Q,R,S$ kaki-kaki garis tegak lurus dari $Y$ ke garis $AX, BX, AZ, BZ$. Buktikan bahwa sudut lancip yang dibentuk oleh garis $PQ$ dan $RS$ adalah setengah dari besar sudut $\angle XOZ$, dengan $O$ adalah titik tengah ruas garis $AB$.
Solusi:
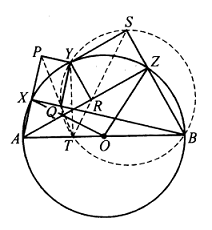
Seperti yang ditunjukkan dalam diagram, Misalkan $T$ adalah kaki garis tegak lurus dari $Y$ ke $AB$, maka, berdasarkan teorema Simson, $P,Q,T$ segaris dan demikian pula $S,R,T$. Maka $$\angle YQB=\angle YTB=\angle YSB=90^o,$$ $S,Y,Q,T,B$ konsiklik, sehingga $$\angle PTS=\angle QTS=\angle QBS=\angle XBZ=\frac{1}{2}\angle XOZ.$$ - Diberikan segi empat cembung $ABCD$ dengan $\angle B+\angle D<180^o$, $P$ adalah titik variabel pada bidang yang sama. Misalkan $f(P)=PA\cdot BC+PD\cdot CA+PC\cdot AB$. Buktikan bahwa $P, A, B, C$ konsiklik jika $f(P)$ mencapai nilai minimumnya.
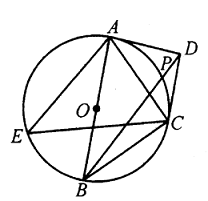
Solusi: Seperti pada gambar, untuk setiap titik $P$ pada bidang, ketidaksaam Ptolemeus memberikan $$PA\cdot BC+PC\cdot AB\ge AC,$$ oleh karena itu $$f(P)=PA\cdot BC+PC\cdot AB+PD\cdot CA$$ $$\ge PB\cdot CA+PD\cdot CA$$ $$=(PB+PD)\cdot CA\ge BD\cdot CA,$$ dimana persamaan berlaku jika dan hanya jika $PABC$ siklik. Oleh karena itu $f(P)$ mempunyai batas bawah $BD\cdot AC$. Akan tetapi, batas ini dapat dicapai jika dan hanya jika $P$ adalah titik perpotongan lingkaran luar $\Delta ABC$ dan ruas garis $BD$, sehingga $P, A, B, C$ bersifat konsiklis. - (Teorema Pascal) Jika suatu segi enam $ABCDEF$ tertulis di dalam suatu lingkaran sedemikian rupa sehingga garis $AB$ dan $ED$ yang dihasilkan berpotongan di $H$, garis $BC$ dan $FE$ yang dihasilkan berpotongan di $K$, dan garis $AF$ dan $CD$ yang dihasilkan berpotongan di $I$, buktikan bahwa $H, K, I$ segaris.
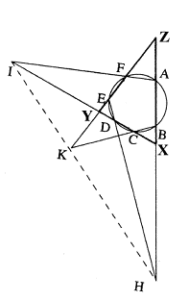
Solusi: Misalkan garis $AB, CD, EF$ membentuk $\Delta XYZ$. Dengan menganggap garis $AFI, BCK, HDE$ sebagai tiga garis transversal $\Delta XYZ$, maka Teorema Menelaus menghasilkan $$\frac{XA}{AZ}\cdot \frac{ZF}{FY}\cdot \frac{YI}{IX}=1,$$ $$\frac{XB}{BZ}\cdot \frac{ZK}{KY}\cdot \frac{YC}{CX}=1,$$ $$\frac{XH}{HZ}\cdot \frac{ZE}{EY}\cdot \frac{YD}{DX}=1.$$ Mengalikan tiga persamaan dan mempertimbangkannya $$XA\cdot XB=XC\cdot XD,\text{ }\text{ }YC\cdot YD=YE\cdot YF$$ dan $ZE\cdot ZF=ZA\cdot ZB$, kita peroleh $\frac{YI}{IX}\cdot \frac{XH}{HZ}\cdot \frac{ZK}{KY}=1$. Dengan Teorema Meneleus invers, $I,K,H$ kolinear. - (Teorema Pappus) Diketahui $A, B, C$ adalah tiga titik pada garis $\mathscr{l}_1$ dan $a, b, c$ adalah tiga titik pada garis $\mathscr{l}_2$ lainnya. Jika ruas garis $Ab$ dan $Ba$ berpotongan di $N$, ruas garis $Ac$ dan $Ca$ berpotongan di $L$, dan ruas garis $Bc$ dan $Cb$ berpotongan di $M$, buktikan bahwa $N, L, M$ kolinear.
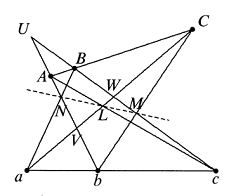
Solusi: Mempertimbangkan segitiga $UVW$ yang dibentuk dengan garis $Ab,aC,Bc$, seperti yang ditunjukkkan pada gambar. Ada lima lintang: $$ALc,CMb,aNB,CBA,abc.$$ Menerapkan teorema Meneleus menghasilkan $$\frac{VL}{LW}\cdot \frac{Wc}{cU}\cdot \frac{UA}{AV}=1,$$ $$\frac{VC}{CW}\cdot \frac{WM}{MU}\cdot \frac{Ub}{bV}=1,$$ $$\frac{Va}{aW}\cdot \frac{WB}{BU}\cdot \frac{UN}{NV}=1,$$ $$\frac{VC}{CW}\cdot\frac{WB}{BU}\cdot\frac{UA}{AV}=1\text{ dan }\frac{Va}{aW}\cdot \frac{Wc}{cU}\cdot \frac{Ub}{bV}=1.$$ Dengan mengalikan tiga persamaan pertama dan kemudian membagi persamaan yang dihasilkan dengan hasil perkalian dua persamaan terakhir, maka diperoleh: $$\frac{VL}{LW}\cdot \frac{WM}{MU}\cdot \frac{UN}{NV}=1.$$ Maka, dengan teorema Meneleus invers, $L,N,M$ kolinear. - $ABCD$ adalah segi empat yang sinar-sinarnya $BA$ dan $CD$ berpotongan di $E$, dan sinar-sinarnya $AD$ dan $BC$ berpotongan di $F$. Misalkan $N, L, M$ masing-masing adalah titik tengah $EF, AC, BD$. Buktikan bahwa $N, L, M$ kolinear.
Catatan: Garis yan melalui $N,L,M$ disebut Garis Newton pada segiempat $ABCD$.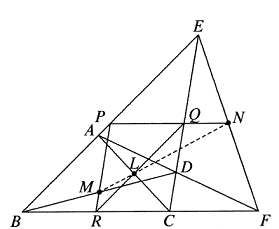
Solusi: Misalkan titik tengah $EB,EC,BC$ masing-masing adalah $P,Q,R$. Maka teorema titik tengah mengindikasi bahwa $Q,L,R$ kolinear, dan $$\frac{QL}{LR}=\frac{EA}{AB}.$$ Demikian pula, $P,M,R$ kolinear, dan $$\frac{RM}{MP}=\frac{CD}{DE}.$$ Di samping itu, $N,Q,P$ kolinear, dan $$\frac{PN}{NQ}=\frac{BF}{FC}.$$ Menerapkan teorema Meneleus ke $\Delta EBC$ dan lintang $ADF$ maka memberikan $$\frac{EA}{AB}\cdot\frac{BF}{FC}\cdot \frac{CD}{DE}=1,$$ oleh karena itu $\frac{QL}{LR}\cdot \frac{RM}{MP}\cdot\frac{PN}{NQ}=\frac{EA}{AB}\cdot\frac{CD}{DE}\cdot\frac{BF}{FC}=1$. Dengan menerapkan teorema Meneleus invers ke $\Delta PQR$ dan tiga titik $M,L,N$, kesimpulan $M,L,Q$ kolinear terbukti.
Solusi dari setiap Permasalahan diberikan pada kelas online
“Leadership is not about titles, positions, or flowcharts. It is about one life influencing another.”

