- Diberikan dua barisan aritmatika tak konstan $a_{1},a_{2},…$ dan $b_{1}.b_{2},…$ Jika $a_{228}=b_{15}$ dan $a_{8}=b_{5}$. Tentukan nilai dari $\frac{b_{4}-b_{3}}{a_{2}-a_{1}}$.
- Tentukan banyaknya bilangan asli $n \le 221$ sehingga $\frac{1^{2}+2^{2}+…..+n^{2}}{1+2+…..+n}$ merupakan bilangan bulat.
- Tentukan banyaknya garis berbeda pada koordinat kartesius yang dapat diambil dari pasangan $(a,b)\in \{ 0,1,2,3,6,7 \}$ sehingga memenuhi $ax+by=0$.
- Diberikan persegi panjang $ABCD$ dan segitiga sama sisi $BCP$ dan $CDQ$ seperti gambar di bawah ini.
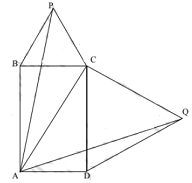
Jika panjang $AB=8, AC=10$ dan luas segitiga $ACP$ ditambah luas segitiga $ACQ$ dapat dinyatakan dalam bentuk $m\sqrt{3+n}$, tentukan nilai $m+n$. - Diberikan himpunan $S = \{ 1,5,6,7,9,10,11,13,15,20,27,45 \}$. Tentukan banyaknya himpunan bagian 3 anggota sehingga hasil kali ketiga bilangan tersebut habis dibagi 18.
- Perhatikan lingkaran pada gambar berikut ini.
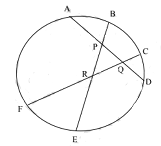
Jika diketahui panjang $AP = 22, CQ = 14$ dan $ER = 35$ serta segitiga $PQR$ sama sisi, tentukan nilai $BP + QD + RF$. - Tentukan banyaknya bilangan asli $n$ sehingga $$\sqrt{2n-12}+\sqrt{2n+40}$$ adalah bilangan asli.
- Diberikan bilangan real $a, b$ sehingga memenuhi kedua persamaan berikut $$\frac{1}{a}+\frac{1}{b}\le 2\sqrt{\frac{3}{7}}\text{ dan }(a-b)^{2}=\frac{9}{49}(ab)^{3}$$ Tentukan nilai maksimum dari $a^{2}+b^{2}$.
- Misalkan $ABCD$ adalah suatu persegi dengan panjang sisi 43 cm dan titik-titik $X$ dan $Y$ berturut-turut terletak pada sisi $AD$ dan $BC$ sehingga perbandingan luas $ABXY$ dengan luas $CDXY$ adalah 20 : 23. Tentukan panjang maksimum $XY$ yang mungkin.
- Misalkan $K$ suatu bilangan asli sehingga terdapat tripel bilangan $(x,y,z)$ dengan $$x^{3}+Ky,y^{3}+Kz$$ dan $$z^{3}+Kx$$ Semuanya merupakan bilangan kubik sempurna.
a. Buktikan bahwa $K\neq 2$ dan $K\neq 4$
b. Tentukan bilangan asli $K$ terkecil yang memenuhi syarat di atas, jelaskan jawaban anda.
Catatan: Bilangan kubik sempurna adalah bilangan bulat berbentuk $n^{3}$ dengan $n$ bilangan bulat. - Tentukan bilangan bulat terbesar $B$ sehingga untuk setiap 9 bilangan asli berbeda yang hasil penjumlahannya 2023, pasti terdapat 4 diantaranya yang hasil penjumlahannya minimal $B$.
- Tentukan semua bilangan real tak rasional $\alpha$ yang memenuhi $$\alpha^{3}-15\alpha\text{ dan }\alpha^{4}-56\alpha$$ Keduanya merupakan bilangan rasional.
- Diberikan segitiga $ABC$ dan titik $D$ dan $E$ terletak pada sisi $BC$. Titik $X$ dan $Y$ terletak di dalam segitiga $ABC$ sehingga berlaku
$$\angle BXE+\angle BCA= \angle CYD+\angle CBA= 180\circ$$
Misalkan garis $AD$ memotong garis $XE$ di titik $P$ dan garis $YD$ di titik $Q$. Jika diketahui bahwa $X,Y,D,E$ terletak pada satu lingkaran, buktikan bahwa garis $BP$, garis $CQ$ dan garis sumbu sisi $BC$ berpotongan pada satu titik.
Keranjang Belanja
