- Diberikan segitiga sama kaki $ABC$ dengan $AB = AC$. Misalkan garis bagi sudut $ABC$ memotong $AC$ di titik $D$ sehingga $BC = BD+AD$. Besar sudut $CAB$ adalah …
- Jika $n$ bilangan asli dan $\frac{1}{2}+\frac{1}{3}+\frac{1}{5}-\frac{1}{n}$ merupakan bilangan bulat, maka pembagi positif dari $n$ sebanyak …
- Jika $a \ge b > 1$, maka nilai terbesar yang mungkin untuk $a_{\log}\left( \frac{a}{b} \right)+b_{\log}\left( \frac{b}{a} \right)$ adalah …
- Diketahui segi empat $ABCD$. Semua titik $A, B, C$ dan $D$ akan diberi nomor 1, 2, 3, 4, 5 atau 6 sehingga setiap dua titik yang terletak dalam satu sisi empat nomornya berbeda. Banyaknya cara pemberian nomor dengan cara tersebut ada sebanyak …
- Diberikan fungsi $f$ dengan $f(x) = \sqrt{ax^{2} + x}$. Semua nilai $a$ yang mungkin sehingga domain dan daerah hasil $f$ sama adalah …
- Banyaknya kemungkinan bilangan asli berbeda $a, b, c$ dan $d$ yang kurang dari 10 dan memenuhi persamaan $a + b = c + d$ ada sebanyak …
- Jika kedua akar persamaan $x^{2} − 2013x + k = 0$ adalah bilangan prima, maka nilai $k$ yang mungkin adalah …
- Jika $$\left( 1-\tan^{2}\frac{x}{2^{2011}} \right)\left( 1-\tan^{2}\frac{x}{2^{2010}} \right)…\left( 1-\tan^{2}\frac{x}{2} \right)=2^{2011}\sqrt{3}\tan\frac{x}{2^{2011}}$$ maka $\sin 2x$ adalah …
- Pada ruang Cartesius kita ingin bergerak dari titik (2, 0, 11) ke titik (20, 1, 1) selalu pada koordinat $(x, y, z)$ dengan paling sedikit dua dari $x, y$ dan $z$ adalah bilangan bulat, dan lintasan terpendek. Cara bergerak yang dimaksud sebanyak …
- Misalkan $x, y$ dan $z$ adalah bilangan real positif dengan sifat $xyz = 1$. Nilai terkecil dari $$(x+2y)(y+2z)(xz+1)$$ tercapai saat $x+y+z$ bernilai …
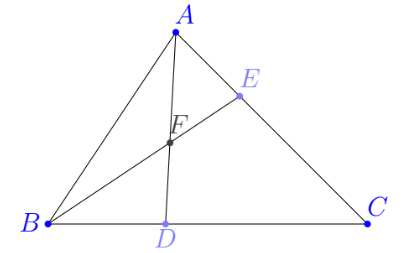
- Pada gambar di bawah ini, panjang $AE = x, EC = y$ dan $DC = 2BD$. Perbandingan panjang $BF$ dan $FE$ dinyatakan dalam $x$ dan $y$ adalah …
- Banyaknya bilangan tiga digit yang semua digit – digitnya berbeda dan digit terakhir merupakan hasil penjumlahan dari dua digit yang lainnya adalah …
- Diberikan barisan bilangan rasional $\{ a_{k} \}_{k\in \mathbb{N}}$ yang didefinisikan dengan $a_1 = 2$ dan $$a_{n+1}=\frac{a_{n-1}}{a_{n+1}},\mathcal{n}\in \mathbb{N}$$ Nilai $a_{2011}$ adalah …
- Misalkan $\Gamma$ lingkaran luar segitiga $ABC$. Talibusur $AD$ adalah garis bagi $\angle BAC$ yang memotong $BC$ di titik $L$. Talibusur $DK$ tegak lurus pada $AC$ dan memotongnya di titik $M$. Jika $\frac{BL}{BC} =\frac{1}{2}$, maka perbandingan $\frac{AM}{MC}$ = …
- Dua dadu memiliki angka 1 sampai 6 yang dapat dilepas dari dadu. Kedua belas angka tersebut dilepas dari dadu dan dimasukkan ke dalam suatu kantong. Secara acak diambil satu angka dan dipasangkan ke salah satu dari kedua dadu tersebut. Setelah semua angka terpasangkan, kedua dadu dilemparkan secara bersamaan. Peluang munculnya angka tujuh sebagai jumlah dari angka pada bagian atas kedua dadu tersebut adalah …
- Banyaknya bilangan asli $n$ sehingga setiap titik dengan koordinat bilangan asli yang terletak pada garis $x+y = n$ mempunyai jarak suatu bilangan prima terhadap titik pusat $(0, 0)$ adalah …
- Bilangan asli $n$ yang memenuhi $(−2004)^{n} − 1900^{n} + 25^{n} − 121^{n}$ habis dibagi 2000 adalah …
- Sepuluh orang siswa duduk dalam suatu baris. Semua siswa bangkit dan duduk kembali pada baris tersebut dengan aturan setiap siswa dapat duduk kembali pada kursi yang sama atau pada kursi yang berada di sebelah kursi lamanya. Banyaknya cara semua siswa tersebut duduk kembali pada baris tadi ada sebanyak …
- Bilangan asli terbesar $n \le 123456$ sehingga terdapat bilangan asli $x$ dengan sifat jumlah semua digit dari $x^{2}$ sama dengan $n$ adalah …
- Misalkan $ABC$ suatu segitiga dan $P$ titik di dalam segitiga. Misalkan $D, E, F$ berturut – turut titik di sisi – sisi $BC, CA, AB$ sedemikian sehingga $PD$ tegak lurus $BC, PE$ tegak lurus $CA$, dan $PF$ tegak lurus $AB$. Jika segitiga $DEF$ sama sisi dan $\angle APB = 70◦$, maka $\angle ACB$ = …
Keranjang Belanja
