- Misalkan $f(x) = a^{2}x + 200$.
Jika $f(20) + f^{-1}(22) = f^{-1}(20)+f(22),$
Maka $f(1)$ = … - Banyaknya bilangan bulat dari 1001 sampai dengan 2022 yang habis dibagi 12 atau 18 adalah …
- Diberikan segitiga $ABC$ siku-siku disudut $B$. Titik $D$ berada pada sisi $AB$ dan titik $E$ berada pada sisi $AC$. Diketahui bahwa $DE$ sejajar dengan $BC$. Jika $AD = 18, DB = 3$ dan $BC = 28$, maka panjang $AE$ adalah …
- Banyaknya pasangan bilangan bulat $(x,y)$ yang memenuhi persamaan $$|x| + |y| +|x+y| = 22$$ adalah …
- Jika sisa pembagian $$x^{2023}+x^{1012}+x^{506}+x^{253}+x^{127}$$ oleh $x^{2}-1$ adalah $Ax+B$, maka nilai dari $34+4B$ = …
- Sebuah papan catur persegi panjang berukuran 3 x 20 akan ditutupi dengan 20 tromino seperti pada gambar dibawah ini sehingga seluruh papan catur tertutupi oleh seluruh tromino dan tidak ada tromino yang tumpang tindih. Banyaknya cara untuk melakukan hal tersebut adalah …
- Diberikan segitiga $ABC$ seperti pada gambar dibawah.
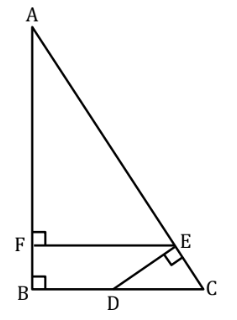
Diketahui $AB = \frac{3}{2}BC$ dan $BD=CD$, Jika luas segitiga $DEC$ adalah 13, maka luas segitiga $AFE$ adalah …
- Untuk setiap bilangan asli $n$, Misalkan $S(n)$ menyatakan hasil penjumlahan semua digit $n$. Diberikan barisan $(a_{n})$ dengan $a_{1}=4$ dan $a_{n}=(S(a_{n-1}))^{2}-1$ untuk $n\ge 2$. Sisa pembagian $a_{1}=a_{2}+a_{3}+…+a_{2022}$ oleh 21 adalah …
- Misalkan $x$ dan $y$ bilangan real dengan $x>y>0$. Jika $x+200 \le \sqrt{x^{2}-y^{2}+400(x+y)}$, maka $y$ = …
- Jika $x$ adalah bilangan asli sehingga $x^{2}+42x$ merupakan pangkat tiga dari suatu bilangan prima, maka $x$ = …
- Didalam suatu ruangan terdapat 12 kursi yang disusun dalam tiga baris, sehingga baris pertama memuat 3 kursi, baris kedua memuat 4 kursi dan baris terakhir memuat 5 kursi. 12 siswa termasuk Azka dan Budi akan menempati kursi-kursi tersebut. Jika banyaknya cara menempati sehingga Azka dan Budi di baris pertama adalah A maka $\frac{A}{9!}$ = …
- Diketahui segitiga $ABC$ merupakan segitiga siku-siku dengan luas 63. Misalkan $R$ dan $r$ berturut-turut menyatakan panjang jari-jari lingkaran luar dan jari-jari lingkaran dalam segitiga $ABC$. Jika $R+r= 12$, maka panjang sisi miring dari $ABC$ adalah …
- Jika $$\sum_{k=1}^{\infty }\frac{2k+B}{3^{k+1}}=20$$ maka $B$ adalah …
- Banyaknya tripel $(w_{1},w_{2},w_{3},…,w_{7})$ yang memenuhi persamaan $$w_{1},w_{2},w_{3},…,w_{7}=148$$ dengan $20\le w_{1},w_{2},w_{3},…,w_{7} \le 22$ adalah …
- Diberikan segitiga siku-siku sama kaki $ABC$ dengan $BC=AB$. Misalkan $L$ titik tengah $BC$ dan $P$ titik pada sisi $AC$ sehingga $BP$ tegak lurus $AL$. Jika $CP=20 \sqrt{2}$, maka panjang $AB$ adalah …
- Misalkan $m$ dan $n$ bilangan-bilangan asli. Jika $FPB(m,n)=3$ dan $FBP(2m,5n)=30$, maka $FPB(15m,6n)$ adalah …
- Diketahui $a,b,c,d$ bilangan real positif yang memenuhi $a>c,d>b$ dan $$3a^{2}+3b^{2}=3c^{2}+3d^{2}=4ac+4bd$$ Nilai $\frac{12(ab+cd)}{(ad+bc)}$= …
- Misalkan $A$ adalah himpunan semua bilangan 8 digit yang digit-digitnya adalah 1,2 atau 3 dan memuat paling sedikit 1 digit 2. Banyaknya bilangan $N$ di $A$ sehingga setiap digit 2 di $N$ diapit oleh digit 1 dan 3 adalah …
- Diberikan suatu belah ketupat $ABCD$ dan sebuah titik $E$ di dalamnya, sehingga $AE =BE$. Jika $\angle BAE=12\circ$ dan $\angle DAE = 72 \circ$, maka $\angle CDE$ = …
- Diketahui $x,y,z$ adalah bilangan bulat yang memenuhi $$x^{2}y+y^{2}z+z^{2}x-20=xy^{2}+yz^{2}+zx^{2}-22=3xyz$$ Nilai terbesar dari $x+y+z$ adalah …
Keranjang Belanja
