- Misal $u_{1}, u_{2}, u_{3},…$ barisan aritmatika dengan suku-suku real positif. Jika $\frac{u_{1}+u_{2}}{u_{3}}=\frac{11}{21}$, maka nilai $\frac{u_{2}+u_{3}}{u_{1}}$ adalah …
- Koefisien $x^{7}$ pada penjabaran $$(1+x)(2+x^{2})(3+x^{3})(4+x^{4})(5+x^{5})$$ adalah …
- Diberikan fungsi $f$ terdefinisi untuk semua bilangan real $x$ selain 0 dan 1, memenuhi $$(x+1)f(-x)+\frac{1-x}{4x}f\left( \frac{1}{x} \right)=\frac{100(x^{2}+4)}{x}$$ Hitung nilai dari $f(2)+f(3)+f(4)+…+f(400)$.
- Diketahui bilangan bulat positif $A$ dan $B$ jika dibagi 5 berturut-turut bersisa 2 dan 3. Sisa pembagian bilangan $A(A+ 1) + 5B$ oleh 25 adalah …
- Bilangan asli $n$ dikatakan menarik jika terdapat suku banyak (polinom) dengan koefisien bilangan bulat $P(x)$ sehingga $P(7) = 2021$ dan $P(n) = 2045$. Banyaknya bilangan prima menarik adalah …
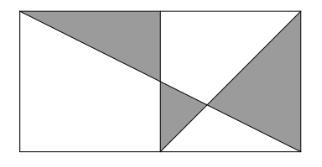
- Pada gambar di bawah ini, sebuah persegi panjang dibagi dua menjadi 2 buah persegi yang panjang sisinya 6 cm. Luas total daerah yang diarsir adalah … $cm^{2}$.
- Pada suatu lingkaran dengan jari-jari $r$, terdapat segiempat talibusur $ABCD$ dengan $AB = 8$ dan $CD = 5$. Sisi $AB$ dan $DC$ diperpanjang dan berpotongan di luar lingkaran di titik $P$. Jika $\angle APD = 60^o$ dan $BP = 6$, maka nilai dari $r^{2}$ adalah …
- Bilangan $1,2,3,… ,999$ digit-digitnya disusun membentuk angka baru $m$ dengan menuliskan semua digit bilangan-bilangan tadi dari kiri ke kanan. Jadi, $m = 1234… 91011 … 999$. Hasil penjumlahan digit ke-2021, 2022, 2023 dari $m$ adalah …
- Diketahui ada 6 pasang suami-istri. Dari keenam pasangan tersebut, dipilih 6 orang secara acak. Banyaknya cara untuk memilih 6 orang tersebut sehingga paling banyak terdapat sepasang suami-istri adalah …
- Diketahui segitiga $ABC$ dengan $AB>AC$. Garis bagi sudut $BAC$ memotong $BC$ di titik $D$. Titik $E$ dan $F$ berturut-turut terletak pada sisi $AC$ dan $AB$ sehingga $DE$ sejajar $AB$ dan $DF$ sejajar $AC$. Lingkaran luar $\Delta BCE$ memotong sisi $AB$ di titik $K$. Jika luas segitiga $CDE$ adalah 75 dan luas segitiga $DEF$ adalah 85, maka luas segiempat $DEKF$ adalah …
- Jika $a > 1$ suatu bilangan asli sehingga hasil penjumlahan semua bilangan real $x$ yang memenuhi persamaan $$\left\lfloor x \right\rfloor^{2}-2ax+a=0$$ adalah 51, maka $a$ adalah … Catatan: $\left\lfloor x \right\rfloor$ menyatakan bilangan bulat terbesar yang tidak lebih dari $x$.
- Diketahui bilangan real $a, b$ dan $c$ memenuhi pertidaksamaan $$|ax^{2}+bx+c|\le 1$$ untuk setiap $x$ anggota bilangan real dengan $0 \le x \le 1$. Nilai maksimum yang mungkin dari $21a+20b+19c$ adalah …
- Diberikan $x, y$ dan $n$ bilangan asli yang memenuhi $$x^{2}+(y+2)x+(n+1)y=n^{2}+252$$ Nilai $y$ terbesar yang mungkin adalah …
- Jika dua digit terakhir dari $a^{777}$ adalah 77, maka dua digit terkahir dari $a$ adalah …
- Bilangan asli ganjil $b$ terbesar sehingga barisan bilangan asli $$a_{n}=n^{2}+19n+b$$ memenuhi FPB$(a_{n},a_{n+1})$=FPB$(a_{n+2},a_{n+1})$ untuk setiap bilangan asli $n$ adalah …
- Diberikan segitiga $ABC$ dengan $AB = 6, BC = 7$ dan $CA = 8$. Jika $I$ adalah titik potong ketiga garis bagi segitiga $ABC$, maka $AI^{2}$ adalah …
- Banyak fungsi (pemetaan) dari $A = \{1, 2, 3, 4, 5,6\}$ ke $B = \{7, 8, 9, 10\}$ dengan syarat 7 dan 8 mempunyai prapeta, yaitu ada $x$ dan $y$ di $A$ sehingga $f (x) = 7$ dan $f(y) = 8$ adalah …
- Banyaknya barisan ternary (sukunya 0, 1 atau 2) yang memuat 13 suku, memuat tepat empat 0 dan setiap di antara dua 0 ada paling sedikit dua suku bukan 0 adalah …
- Sebuah papan catur berukuran $101\times 21$ akan dipasangi beberapa ubin berukuran $3\times 1$. Berapa ubin terbanyak yang bisa dipasang pada papan sehingga tidak ada 2 ubin yang bertumpuk atau bersentuhan? (Bersentuhan pada titik sudut ubin juga tidak diperbolehkan)
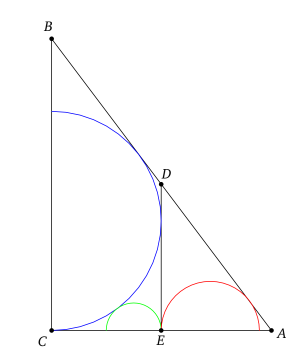
- Diberikan segitiga siku-siku $ABC$, dengan $\angle C=90^o$. Titik $D$ terletak pada sisi $AB$ dan $E$ pada sisi $AC$ sehingga garis $DE$ sejajar dengan garis $BC$. Diketahui tiga setengah lingkaran berwarna biru, merah dan hijau sedemikian sehingga setengah lingkaran biru menyinggung $AC$ dan $AB$, setengah lingkaran merah menyinggung sisi $AB$ dan garis $DE$, dan setengah lingkaran hijau menyinggung setengah lingkaran biru dan garis $DE$ (perhatikan gambar berikut).
Jika $2AC+5BC=5AB$, maka perbandingan panjang jari-jari setengah lingkaran merah dengan jari-jari setengah lingkaran hijau adalah $k:25$. Nilai $k$ adalah …
Keranjang Belanja
