- Diketahui angka satuan dari $p^x$ adalah 9 dan angka satuan dari $q^y$ adalah 8. Jika $p$ bilangan ganjil dan $q$ bilangan genap, serta $x$ dan $y$ bilangan bulat, maka banyaknya angka satuan yang mungkin dari $x + y$ adalah …
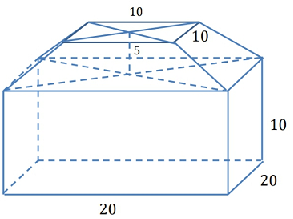
- Suatu penampung air berbentuk gabungan balok dan limas terpancung dengan ukuran dalam meter(m) seperti pada gambar berikut: Penampung tersebut yang semula kosong diisi air dengan debit 1000 $m^3$/jam. Waktu yang dibutuhkan agar air dalam penampung setinggi $20 − 5\sqrt[3]{2}m$ adalah …
- Misalkan $x, y$ dan $z$ adalah bilangan real positif yang memenuhi system persamaan berikut $$x + y + z = 6$$ $$x^2 + y^2 + z^2 = 20$$ $$x^3 + y^3 + z^3 = 72$$
Nilai dari $x^4 + y^4 + z^4$ adalah … - Empat titik berbeda $A, B, C$ dan $D$ terletak pada lingkaran berjari-jari 7 cm. Diketahui $AB: BC = 3: 4, AB = AD$, dan $BC = CD$. Titik $E$ adalah perpotongan $AC$ dan $BD$. Melalui $E$ dibuat garis $k$ dan $l$. Garis $k$ tegak lurus $BC$ dan memotong $AD$ di $P$. Sementara, garis $l$ tegak lurus $AD$ dan memotong $BC$ di $Q$. Perbandingan luas daerah segitiga $AQP$ dan $PQD$ adalah 1 ∶ …
- Jika $x$ merupakan akar dari $x^2 + x − 1 = 0$, maka nilai $n$ yang memenuhi: $$x^{2023} − x^{2024} = (x(1 − x))^n$$ adalah …
- Suatu permainan dilakukan dengan mengambil tiga bola sekaligus secara acak dari satu kantong yang berisi 31 bola bernomor berbeda, dari 1 sampai 31. Budi akan menang jika ketiga bola yang terambil memenuhi ketiga syarat berikut.
(a) Tidak ada bola nomor 1
(b) Tidak ada bola dengan nomor berurutan
(c) Rata-rata nomor terbesar dan terkecil lebih besar dari median ketiga nomor yang terambil
Jika peluang Budi memenangkan permainan tersebut dapat dinyatakan dalam bentuk pecahan yang paling sederhana $\frac{m}{n}$, maka nilai dari $m + n$ adalah … - Sejumlah $m$ bola merah dan $p$ bola putih akan disusun memanjang secara acak sehingga peluang bola di ujung kiri dan kanan susunan berwarna sama adalah 12. Jika diketahui $4 \le m \le p \le 2023$, maka banyaknya pasangan $(m, p)$ yang mungkin adalah …
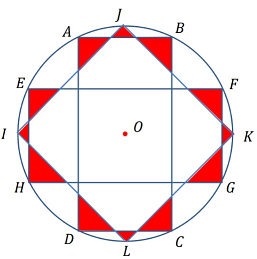
- Di dalam lingkaran berpusat di $O$, dibuat dua persegi panjang kongruen $ABCD$ dan $EFGH$, dimana titik-titik $A, B, C, D, E, F, G, H$ terletak pada lingkaran. Garis $AB$ sejajar $EF, AB = EH =2$ cm, dan $AD = EF = 4$ cm. Di dalam lingkaran tersebut juga dibuat persegi $IJKL$, dimana titik-titik $I, J, K, L$ terletak pada lingkaran dan diagonal $LJ$ sejajar $AB$. Jika jumlah luas daerah semua segitiga yang berwarna merah adalah $a + b\sqrt{5}$ $cm^2$, maka nilai dari $a − b$ adalah …
- Suatu kerucut memiliki jari-jari alas 3 cm dan panjang sisi miring 5 cm. kerucut tersebut dicelupkan dalam posisi tegak ke dalam suatu wadah cukup besar yang berisi cat. Pada saat keseluruhan alas kerucut menyentuh alas wadah cat, ketinggian cat pada wadah adalah 2 cm, sehingga sebagian kerucut akan tertutup cat. Jika perbandingan luas permukaan yang tertutup cat terhadap keseluruhan permukaan kerucut dapat dinyatakan dalam pecahan paling sederhana $\frac{a}{b}$, maka nilai dari $a + b$ adalah …
Dari hasil itu diperoleh $a = 27$ dan $b = 32$. Jadi, $a + b = 27 + 32 = 59$. - Didefinisikan $f(n)$ sebagai jumlah semua digit pada bilangan bulat $n$. Banyaknya bilangan bulat $n$ dengan $100 \le n \le 999$ dan $9 \le f(n) \le 12$ adalah …
- Diketahui fungsi-fungsi $F_1(x), F_2(x), F_3(x), … , F_1000(x)$, dengan $F_1(x) = x$, dan untuk $n \ge 1$ $$F_{n+1}(x) =\frac{1}{1 − F_n(x)}$$ Jika $K$ adalah bilangan genap tiga digit dan $F_K(K) = K$, maka banyaknya semua nilai $K$ yang mungkin adalah …
- Pak Andi merupakan salah satu dari 7 calon guru yang berpeluang sama untuk ditempatkan di salah satu sekolah, SMP X atau SMP Y. SMP X membutuhkan 2 guru baru, sedangkan SMP Y membutuhkan 3 guru baru. Jika peluang Pak Andi ditempatkan di SMP X adalah $\frac{a}{35}$ maka nilai $a$ adalah …
- Diketahui segitiga $ABC$ dengan panjang sisi $AB = 20$ cm. Titik $P$ berada pada sisi $AB$ sehingga $AP = BP = CP$. Luas daerah segitiga $APC$ adalah 30 $cm^2$. Jika jarak titik $P$ ke sisi $BC$ adalah $d$ cm, maka nilai terbesar $d^2$ yang mungkin adalah …
- Bilangan bulat $a$ memenuhi persamaan berikut. $$1+\frac{1}{2}+\frac{1}{3}+ ⋯ +\frac{1}{13} = \frac{a}{1 \text{ x } 2 \text{ × } 3 \frac{ × } … \text{ × } 13}$$ Sisa pembagian $a$ oleh 7 adalah …
- Empat puluh dua bilangan berbeda disusun dalam kotak papan dengan 7 baris dan 6 kolom. Banyaknya cara untuk memilih tiga bilangan yang berasal dari baris dan kolom berbeda adalah …
- Bilangan real $x$ memenuhi persamaan berikut. $$\sqrt{2x + \sqrt{2x}} − \sqrt{2x − \sqrt{2x}} = \frac{1}{2}\sqrt{\frac{2x}{2x − \sqrt{2x}}}$$ Nilai dari $32x$ adalah …
- Enam belas titik disusun dalam 4 baris dan 4 kolom sedemikian sehingga jarak antar titik dalam satu baris dan dalam satu kolom sama. Jika dipilih tiga titik secara acak, banyaknya kemungkinan bahwa ketiga titik tersebut membentuk suatu segitiga ketika dihubungkan adalah …
- Bilangan bulat terbesar $n$ dengan $200 < n < 257$ dan $12n$ merupakan bilangan kuadrat adalah …
- Diketahui segitiga sama sisi ABC dengan panjang sisi 10 cm. Suatu lingkaran menyinggung sisi $AB$ dan $AC$ masing-masing di titik $F$ dan $G$. Lingkaran tersebut juga menyinggung lingkaran luar segitiga $ABC$ di titik $H$. Jika luas daerah segitiga $AFG$ adalah $a\sqrt{3}$ $cm^2$, maka nilai dari $9a$ adalah …
- Bilangan bulat $a, b$ dan $c$ memenuhi $$a^3 − b^3 − c^3 = 3abc,$$ $$a^2 = 6(b + c) \text{ dan}$$ $$a^2 + b^2 + c^2 \neq bc − a(b + c)$$ Hasil penjumlahan semua faktor positif dari nilai $a$ terbesar yang mungkin adalah …
Keranjang Belanja
