- Diketahui suatu persamaan $$\frac{a}{b}+\frac{b}{a}= 2021$$ dengan $ab > 1$. Jika nilai terkecil dari $ab$ sehingga $a+b$ merupakan bilangan bulat positif dapat dinyatakan dalam bentuk pecahan yang paling sederhana $\frac{p}{q}$, maka nilai dari $p-q$ adalah …
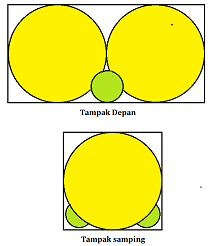
- Seorang anak memiliki 2 bola besar dengan diameter 108 cm dan 2 bola kecil dengan diameter 30 cm. Untuk menyimpannya, dibuatlah kotak transparan dengan ukuran dalam kotak 216 cm x 108 cm x 108 cm. Saat menyimpan, anak tersebut memasukkan 2 bola kecil diikuti dengn 2 bola besar sehingga posisinya seperti terlihat pada dua gambar berikut.
- Banyaknya tripel bilangan bulat positif $(a, b, c)$ yang memenuhi persamaan $$a+b+c = 50$$ dan ketiga pertidaksamaan $a < b + c, b < a + c, c < a + b$ adalah …
- Tujuh orang siswa berprestasi, termasuk Andi dan Budi, diundang menghadiri suatu Talk Show untuk berbagi pengalaman. Karena keterbatasan waktu, panitia hanya memilih lima orang dari ketujuh orang tersebut secara acak untuk berbicara secara bergantian di atas panggung. Peluang Andi dan Budi akan terpilih, tetapi dengan diselingi oleh setidaknya 1 pembicara lainnya adalah …
- Jika $a = 15^{642}, b = 5^{1070}$, dan $c = 3^{1712}$ maka bilangan yang terkecil adalah …
- Suatu bilangan $n$ akan dibagi terus menerus 63 sampai menghasilkan bilangan bukan kelipatan 63.
Jika $n = (1 × 2 × 3 × … × 2021)^{2021}$ maka banyaknya pembagian yang akan dilakukan adalah … - Suatu lingkaran diketahui memiliki pusat di titik $P (11, −2)$. Lingkaran tersebut menyinggung paraboal $y = ax^2 + 1$ di suatu titik $A(x,y)$ pada kuadran I. Jika diketahui pula bahwa suatu garis lurus $y = 3x$ menyinggung parabola di titik $A$ yang sama, maka nilai $a$ adalah …
- Perhatikan gambar berikut !
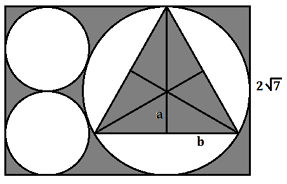
Di dalam lingkaran besar terdapat sebuah segitiga sama sisi dengan $a+b = 3$. Jika perbandingan panjang dan lebar persegi panjang 3 : 2, maka luas daerah yang di arsir adalah … (Gunakan $\pi = \frac{22}{7}$). - Pada suatu kotak terdapat beberapa bola bernomor. Nomor pada bola-bola tersebut terdiri dari faktor prima dari 102021, serta bilangan asli dari persamaan polinomial berikut. $$x^4 − 31x^3 + 321x^2 − 1241x + 1430 = 0$$
Jika dari kotak tersebut diambil 3 bola secar acak, maka peluang jumlah ketiga nomor pada bola berupa bilangan genap adalah … - Jika $k$ bilangan bulat positif, maka jumlah semua nilai $k$ sedemikian sehingga $\frac{3k^2 − 3k}{2k^2 − 10k + 8}$ juga merupakan bilangan bulat positif adalah …
Keranjang Belanja
