A. ISIAN SINGKAT
- Diketahui $x$ dan $y$ adalah bilangan bulat positif. Salah satu solusi dari $20x+14y=2014$ adalah $(x,y)=(100,1)$. Satu solusi yang lain adalah …
Jika $x$ dan $y$ merupakan bilangan real yang memenuhi $x^2+y^2=1$, maka nilai terbesar perkalian $x$ dan $y$ adalah …
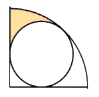
- Sebuah lingkaran berada dalam seperempat lingkaran besar, seperti pada gambar di bawah, jika jari-jari lingkaran besar = 8 satuan, maka luas daerah yang diarsir adalah …
- Jumlah 1007 buah bilangan bulat positif berbeda adalah 1023076. Tidak ada satupun dari bilangan-bilangan tersebut yang lebih besar dari 2014. Minimal banyaknya bilangan ganjil pada deret bilangan tersebut adalah …
- Terdapat bilangan ribuan dengan jumlah angka-angkanya 8. Contoh bilangan ini adalah 1232. Bilangan yang memenuhi sifat ini ada sebanyak …
- Misalkan $ABCD$ adalah suatu daerah trapesium sedemikian sehingga perpanjangan sisi $AD$ dan perpanjangan sisi $BC$ berpotongan di titik $E$. Diketahui panjang $AB=18,CD=30$, dan tinggi trapesium tersebut adalah $8$. Jika $F$ dan $G$ masing-masing adalah titik tengah $AD$ dan $BC$, maka luas segitiga $EFG$ adalah …
- Diberikan dua persamaan berikut. $$\frac{2}{x+y}+\frac{6}{x-y}=2\text{ dan }\frac{4}{x+y}-\frac{9}{x-y}=-1$$ Nilai $\frac{x}{y}$ yang memenuhi kedua persamaan tersebut adalah …
- Jika $a$ dan $b$ bilangan bulat ganjil serta $a>b$, maka banyak bilangan bulat diantara $2a$ dan $b$ adalah …
- Fungsi $g$ dari himpunan $X$ ke himpunan $Y$ dikatakan satu-satu, jika untuk semua $x_1,x_2\in X$ dengan $g(x_1)=g(x_2)$ berlaku $x_1=x_2$. Jika $X=\{9,6,3,2,1\}$ dan $Y=\{1,2,3,4,5,6\}$, maka fungsi berbeda dari $X$ ke $Y$ yang merupakan fungsi satu-satu dan setiap bilangan anggota $X$ tidak dikaitkan dengan faktornya di $Y$ ada sebanyak …
- Indah dan Nian bermain lempar dadu secara bergantian dimulai dengan lemparan pertama giliran Indah. Seseorang akan memenangkan permainan jika ia mendapatkan mata dadu 1 tetapi lawannya tidak mendapatkan mata dadu 2 atau 3 pada lemparan sebelumnya. Peluang Indah pada giliran yang ketiga melempar (lemparan kelima) akan menang adalah …
B. SOAL URAIAN
Temukan semua bilangan real $x$ yang memenuhi persamaan $\sqrt{2-x}>2$.
- Diketahui jumlah $n$ buah bilangan bulat positif ganjil berurutan adalah 5929. Tentukan $n$ terkecil yang mungkin.
- Diberikan kerangka limas $ABCD$ dengan alasnya adalah daerah segitiga siku-siku $ABC$. Diketahui sisi siku-sikunya adalah $AB$ dan $AC$ dengan panjang $AB=a\sqrt{3}$ dan panjang $AC=4a$, rusuk $BD$ tegak lurus dengan bidang $ABC$ dan panjang $BD=6a$. Jika pada rusuk $CD$ terdapat titik $P$ sehingga sebuah bola dengan $DP$ sebagai diameternya menyinggung bidang alas $ABC$, hitung jari-jari bola tersebut.
- Sebuah kode rahasia terdiri dari dua huruf dan satu bilangan antara 100 dan 600. Aturan yang harus dipenuhi adalah sebagai berikut.
(i) Semua angka dan huruf harus saling berbeda,(ii) Jika tiga angka membentuk bilangan genap maka kedua huruf yang dipilih adalah huruf vocal,
(iii) Jika tiga angka membentuk bilangan ganjil maka kedua huruf yang dipilih adalah konsonan.
Tentukan banyak kode rahasia yang mungkin dibuat.
- Untuk $x$ bilangan real, dirumuskan suatu fungsi $f(x)=\frac{2}{2+4^x}$. Maka hitunglah hasil penjumlahan berikut. $$f\left(\frac{1}{2014}\right)+f\left(\frac{2}{2014}\right)+…+f\left(\frac{2013}{2014}\right)$$
