A. ISIAN SINGKAT
- Diketahui segitiga sama sisi dengan panjang sisi 10 cm. Jika dibuat lingkaran yang berpusat titik tengah salah satu sisi segitiga dengan jari-jari 5 cm, maka luas daerah di dalam lingkaran dan di luar segitig adalah … $cm^2$.
- Rata-rata nilai dari 25 siswa adalah 40. Jika selisih rata-rata nilai 5 siswa terendah dan 20 siswa sisanya adalah 25, maka nilai rata-rata 5 siswa terendah adalah …
- Dalam sebuah kotak terdapat beberapa bola dengan empat macam warna yakni: Biru, Merah, Kuning, dan Putih. Paling sedikit terdapat 10 bola untuk masing-masing warna. Bola diambil satu demi satu dari dalam kotak tersebut secara acak tanpa pengembalian. Banyak pengembalian yang harus dilakukan untuk memastikan mendapatkan 6 bola dengan warna yang sama adalah …
- Jika $\frac{x^3+3x^{2}y}{x+3y}-\frac{27y^{3}+9xy^2}{3y+x}=x+3y$, maka nilai $x$ = …
- Himpunan penyelesain pertidaksamaan dibawah adalah … $$\frac{x^4-2x^3-2x^2-1}{x^2-1}\ge 1$$
- Jika nilai $100B=100^2+99^2-98^2-97^2+96^2+95^2-94^2-93^2+…+4^2+3^2-2^2-1$. Maka nilai $B$ adalah …
- Sebuah drum berbentuk tabung yang berjari-jari 70 cm dan berisi air setinggi 40 cm (gunakan $\pi=\frac{22}{7}$), seorang tukang pasang ubin memasukkan 110 buah ubin keramik ke dalam drum sehingga tinggi permukaan air bertambah 8 cm. Jika permukaan setiap ubin keramik berukuran 40 cm x 40 cm, berapakah tebal ubin keramik tersebut?
- Diketahui $n$ bilangan bulat positif. Jika $n$ ditambah angka-angka pembentukannya menghasilkan 313, maka semua nilai $n$ yang mungkin adalah …
- Diketahui 2 buah himpunan $A$ dan $B$ dengan.
$A=\{(x, y)|1987\le y < x \le 2013 \text{ dengan x dan y bilangan bulat }\}$ dan$B=\{(x, y)|y \le 2013 -x \text{ dengan x dan y bilangan bulat }\}$.
Banyaknya anggota himpunan $A-B$ adalah …
- Tim Sepakbola terdiri atas 25 orang, masing-masing diberi kaos bernomor 1 sampai dengan 25. Banyak cara memilih tiga pemain secara acak dengan syarat jumlah nomor kaos mereka habis dibagi tiga adalah …
B. SOAL URAIAN
- Suatu yayasan menyumbangkan 144 buku ke 4 sekolah. Banyak buku yang diterima untuk setiap sekolah tidak sama. Selisih buku yang diterima sekolah $A$ dan $B$ adalah 16. Selisih buku yang diterima sekolah $C$ dan $D$ adalah 8. Sekolah $A$ menerima buku paling sedikit dibandingkan dengan yang diterima sekolah lain. Jika sekolah $D$ menerima buku 2 kali lebih banyak daripada buku yang diterima sekolah $A$, tentukan banyak buku yang diterima masing-masing sekolah.
- Satu set kartu remi/Bridge terdiri dari 52 lembar. Diambil 5 lembar kartu secara acak. Tentukan peluang terambil 2 kartu warna merah dan 3 kartu warna hitam, yang diantaranya terdapat tepat 1 kartu King.
- Misalkan 10 lingkaran yang berjari-jari 1 cm dimasukkan dalam lingkaran berjari-jari $R$ cm seperti pada gambar berikut. Tentukan $R$.
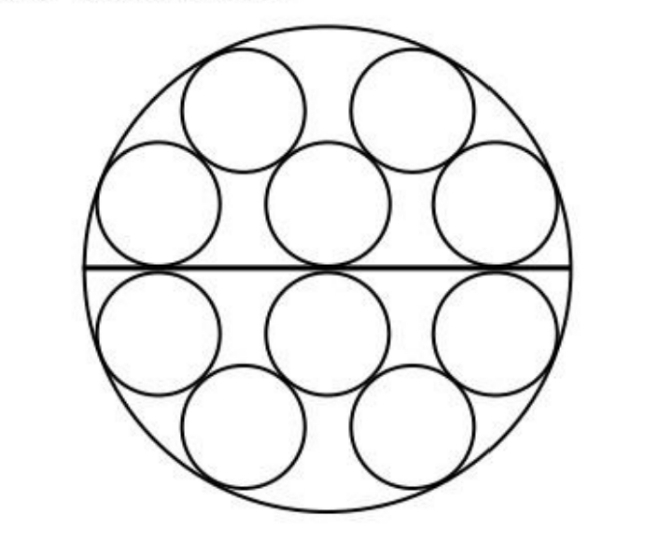
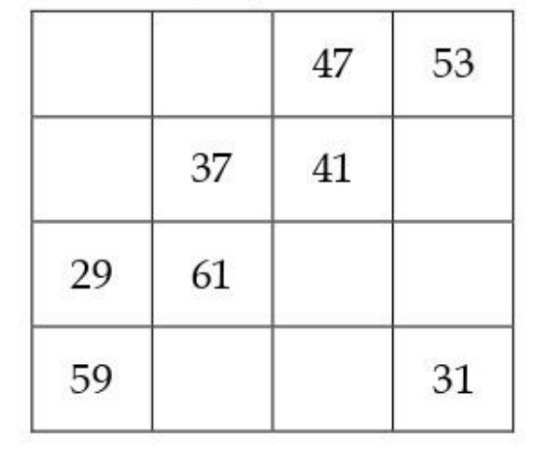
- Gunakan delapan bilangan prima yang berbeda dan kurang dari 25 untuk melengkapi persegi ajaib dibawah, sehingga setiap kotak di dalam persegi terisi oleh satu bilangan prima serta jumlah bilangan pada setiap baris dan setiap kolom selalu sama.
- Didefinisikan $\left[ x \right]$ adalah bilangan bulat terbesar yang kurang dari atau sama dengan $x$. Sebagai contoh $\left[ \frac{5}{2} \right]=2$ karena $2 \le \frac{5}{2} < 3$. Jika $x$ dan $y$ adalah bilangan real dengan $\left[ \sqrt{x} \right]=10$ dan $\left[ \frac{1}{4}\sqrt{y} \right]=8$, tentukan nilai dari $\left[ \sqrt{\left[ \sqrt{x+y} \right]} \right]$.
