- Diberikan segi enam $ABCDEF$ dengan panjang sisi 8 cm. Pada setiap sisi, dibuat setengah lingkaran seperti pada gambar.
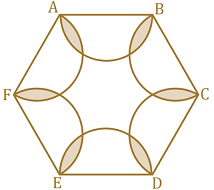
Tentukan luas daerah yang berwarna. - Sebuah segitiga pada koordinat kartesius dikatakan PAS jika titik beratnya pada titik letis. Tentukan nilai $k$ terkecil sehingga jika dipilih $k$ titik letis dengan syarat tidak ada tiga titik yang segaris agar pasti terdapat tiga titik yang membentuk segitiga PAS.
- Bilangan $f_n$ didefinisikan sebagai berikut: $$f_1=2, \text{ }f_2=5, \text{ dan}$$ $$f_n=\frac{1}{2}(f_{n-1}+f_{n-2}), \text{ untuk setiap } n \ge 3$$ Tentukan nilai $f_{2023}+2f_{2024}$.
- Terdapat 2 kelompok bilangan berbeda dengan setiap kelompoknya terdiri dari 2023 bilangan. Kedua kelompok memiliki bilangan pertama $a$, kuartil pertama $b$, median 2023, kuartil ketiga $c$, jangkauan 2023. Kelompok pertama memiliki rata-rata terbesar 2383$\frac{5}{7}$ dan kelompok kedua memiliki rata-rata terkecil $d$ dengan $d$ merupakan bilangan bulat. Tentukan nilai $a,b,c$ dan $d$, jika $b$ merupakan kelipatan 289.
- Didefinisikan sebuah fungsi $g$ dengan $$g(x)=\frac{x}{1-2^x}-\frac{x}{2}$$ untuk setiap $x$ merupakan bilangan real tak nol. Tentukan semua nilai yang mungkin dari $$\frac{g(-x)-g(x)}{g(23)}$$
- Perhatikan pecahan berikut ini.
$$\frac{(10^3-1)(11^3-1)(12^3-1)…(2023^3-1)}{(10^3+1)(11^3+1)(12^3+1)…(2023^3+1)}$$ Jika pecahan tersebut dapat dinyatakan dalam bentuk $$\frac{p(q+1)}{(p+1)q}$$ dengan $p$ dan $q$ bilangan bulat, maka tentukan nilai dari $p$ dan $q$. - Diketahui bilangan real $x,y$ dan $z$ sehingga $$yz=2-x$$ $$xz=\sqrt{2}-\frac{1}{2}y$$ $$xy=-1-\frac{1}{4}z$$ Tentukan semua bilangan $x,y$ dan $z$ yang memenuhi.
- Perhatikan gambar dibawah.
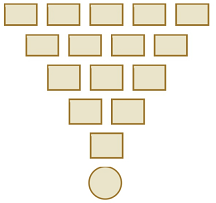
Dipilih lima bilangan dari $\{1,2,3,4,5,6,7,8\}$ dan diletakkan pada lima kotak dibaris paling atas pada gambar. Pada setiap kotak dibawahnya, ditulis bilangan yang merupakan hasil perkalian dari dua kotak di atasnya. Misalkan $x$ merupakan bilangan pada kotak paling bawah. Diketahui $$y=\sqrt{\frac{x}{3}\text{x}10^{-4}}$$ dan $y$ ditulis pada lingkaran paling bawah. Tentukan peluang $y=576$ - Terdapat sebuah kubus $ABCD.EFGH$ yang diletakkan dengan sisi $ABCD$ berada dilantai. Kubus itu diangkat sehingga posisi titik $A$ tetap dan diagonal bidang $ABGH$ tegak lurus lantai. Jarak titik $B$ dan titik $H$ ke lantai adalah 4dan 12 berturut-turut. Kubus itu dipotong menjadi tiga bagian oleh dua bidang sejajar lantai dengan bidang pertama melalui titik $B$ dan bidang kedua berjarak 14 ke lantai. Tentukan volume terbesar dari ketiga bagian tersebut.
- Seseorang memainkan permainan menggunakan dua dadu dengan aturan berikut;
a) Pada langkah pertama dadu dilempar secara bersamaan
b) Jika jumlah mata dadu bernilai 7 atau 11, maka dia menang
c) Jika jumlah mata dadu bernilai 2, 3 atau 12, maka dia kalah
d) Jika jumlah mata dadu tidak bernilai 2, 3, 7, 11 atau 12, maka dia melanjutkan langkah selanjutnya dengan melempar kedua dadu lagi.
e) Jika jumlah mata dadu bernilai 7 atau sama dengan jumlah mata dadu pada lemparan pertama, maka dia menang
f) Jika jumlah mata dadu tidak bernilai 7 dan berbeda dengan jumlah mata dadu pada lemparan pertama, maka lempar kembali kedua dadu dan ulangi lagi mulai pada poin (e)
Tentukan peluang dia memenangkan permainan tersebut.
Keranjang Belanja
