- Misalkan $a$ dan $b$ adalah bilangan real yang memenuhi $a^2 + b^2 \le 1$. Tentukan peluang grafik $f(x) = ax^2 − 2bx − a$ memotong grafik $g(x) = 2x^2$ setidaknya satu titik.
- Danish dan Hamdi memainkan suatu permainan “skuash” yang terdiri dari 5 permainan. Danish bertekad untuk memenangkan setidaknya 2 permainan. Peluang Danish memenangkan suatu permainan adalah 13. Danish dan Hamdi bersepakat jika saat itu Danish memenangkan setidaknya 2 permainan mereka akan berhenti. Jika tidak, mereka akan melakukan 5 permainan tambahan. Pada saat itu mereka melakukan 10 permainan. Peluang Danish memenangkan setidaknya 2 pertandingan?
- Jumlah semua solusi real dari $\sqrt[3]{x − 12} + \sqrt[3]{3x − 16} = \sqrt[3]{2x − 14}$.
- Diberikan barisan bilangan asli
$(n + 1), (n + 2), (n + 3), … … … … , (n + k)$.
Jika suatu bilangan diambil dari barisan tersebut sehingga rata-rata barisannya menjadi $\frac{5055}{100}$, maka berapakah jumlah semua bilangan $k$ yang mungkin? - Diketahui $ABCD$ jajargenjang. Sebuah lingkaran dengan pusatnya pada perpotongan diagonal $AC$ dan $BD$ menyinggung $AB$ dan $CD$. Lingkaran tersebut digeser sehingga menyentuh $BC$. Lingkaran hasil memotong diagonal $BD$ di titik $P$ dan $Q$. Jika $BP = 9, PQ = 27$, dan $DQ = 48$. Tentukan luas daerah jajargenjang yang belum pernah disentuh lingkaran.
- Suatu jarring-jaring laba-laba terbentuk dari komponen berikut.
• Beberapa lingkaran dengan persamaan $x^2 + y^2 = r^2$ dengan jari-jari r = 0, 1, 3, 5, 7, 9 satuan.
• Garis $x = 0, y = 0, x + y = 0, x − y = 0$.
Pergerakan laba-laba memiliki aturan sebagai berikut:
• Pergerakan dari lingkaran yang satu ke lingkaran terdekat dapat dilakukan melalui jaring-jaring yang ada di lingkaran awal atau garis $x = 0, y = 0, x + y = 0$, dan $x − y = 0$, atau
• Membuat lintasan baru dengan menghubungkan suatu titik di jaring-jaring yang sudah ada ke titik ($a, b$) yang terletak pada lingkaran terdekat, dimana $a, b$ bilangan bulat, atau sebaliknya.
• Laba-laba hanya bisa menggunakan lingkaran dan garis di jaring-jaring yang sudah ada maupun lintasan baru satu kali saja. Sebagai contoh, jika misalkan garis $x = 0$ sudah dipergunakan, maka untuk pindah dari satu lingkaran ke lingkaran lain tidak boleh menggunakan garis ini kembali.
• Kecepatan perjalanan melalui jaring-jaring yang sudah ada adalah 1 satuan/menit.
• Kecepatan perjalanan melalui lintasan baru adalah setengah kecepatan perjalanan melalui jaring-jaring yang sudah ada.
Apabila seekor laba-laba berada pada titik (0, 0) dan akan menuju ke lingkaran terluar, tentukan rute dengan durasi tercepat. - Bilangan real $a, b, c$ memenuhi sistem bersamaan berikut:
$ab + ca = 2022 − (a^2 + bc),$
$bc + ca = 7077 − (c^2 + ab),$
$ab + bc = 126 − (b^2 + ca).$
Tentukan semua tripel $(a, b, c)$. - Di suatu semesta alternatif (SA), bilalngan ditulis dengan sistem yang berbeda dengan aturan yang selama ini digunakan di Indonesia. Berikut diberikan beberapa contoh hasil konversi bilangan di Indonesia ke sistem SA tersebut.
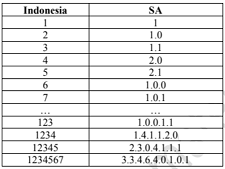
Jika $a(n!)$ Adalah hasil konversi bilangan bulat $n! = n × (n − 1) × (n − 2) × … × 3 × 2 × 1$ ke sistem SA, maka tentukan bilangan bulat terkecil $n$ setelah $n = 1$ yang mengakibatkan banyak digit $n!$ Lebih banyak dari banyaknya titik di $a(n!)$. - Kubus $ABCD.EFGH$ memiliki volume 1 liter. Titik $I$ pada $BF$ dan titik $J$ pada $CG$ sehingga $IJ//BC$. Titik $K$ dan $L$ adalah titik tengah $EH$ dan $FG$ berturut-turut. Titik $O$ pada bidang $IJK$ yang paling dekat ke $L$, jarak $F$ ke garis $IK$ adalah $\frac{5}{2}\sqrt{70}$ cm. tentukan volume limas $L.OIJ$.
- Terdapat sebuah barisan bilangan bulat dengan rata-rata, median, modus, dan jangkauan 2022. Jika $p$ dan $q$ merupakan bilangan terkecil dan terbesar berturut-turut dari barisan tersebut, tentukan banyak pasangan berbeda ($p, q$) yang memenuhi.
Keranjang Belanja
