- Kubus $ABCD.EFGH$ memiliki volume 1000 liter. Garis $l$ terletak pada bidang alas $ABCD$ dan melalui titik pusat $ABCD$, dengan jarak $l$ ke $A$ adalah $30\sqrt{2}$ cm. jika dibuat empat persegi panjang dengan syarat salah satu titik sudut setiap persegi panjang terletak di $l$ dan salah satu sisi setiap persegi panjang adalah rusuk kubus $ABCD.EFGH$ yang berbeda, tentukan jumlah luas minimum keempat persegi panjang tersebut.
- Dari sekumpulan kartu bilangan bulat positif berbeda akan diambil secara bertahan dan ditumpuk satu persatu menjadi satu tumpukan dengan aturan sebagai berikut.
A. Aturan pengambilan
A1. Pengambilan pertama 1 kartu, pengambilan kedua 2 kartu, pengambilan ketiga 3 kartu dan seterusnya.
A2. Kartu yang diambil pada setiap pengambilan (kecuali pengambilan pertama) harus selalu lebih besar dari kartu terbesar di pengambilan sebelumnya.
A3. Setiap pengambilan (kecuali pengambilan pertama) harus berbeda paritasnya dengan pengambilan berikutnya. Maksud paritas berbeda adalah jika pengambilan pertama kartu genap, maka pengambilan kedua harus kartu ganjil semua, pengambilan ketikga harus kartu genap semua, dan begitu seterusnya, serta sebaliknya.
B. Aturan penumpukkan
B1. Proses penumpukan dilakukan setelah proses pengambilan selesai.
B2. Kartu yang lebih kecil tidak boleh berada di atas kartu yang lebih besar.
Proses pengambilan kartu akan dihentikan setelah mendapatkan setidaknya 2021 kartu dan akan dilanjutkan dengan proses penumpukan. Jika kartu yang ditumpuk pertama diberi kode 0001, kartu yang ditumpuk kedua diberi kode 0002, dan seterusnya, maka tentukan bilangan bulat terkecil yang mungkin ada di kartu dengan kode 2021. - Penentuan pemenang suatu permainan dilakukan dengan memutar anak panah pada suatu bidang lingkaran yang dibagi menjadi daerah bernomor seperti pada gambar berikut.
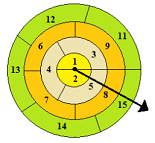
Penyusunan nomor diatur dengan ketentuan berikut.
Lingkaran pertama diagi dalam 2 daerah seimbang dan diberi nomor 1 dan 2.
Lingkaran kedua dibagi dalam 3 daerah seimbang dengan nomor 3, 4, dan 5.
Lingkaran ketiga dibagi dalam 4 daerah seimbang dengan nomor 6, 7, 8, dan 9.
Lingkaran keempat dibagi dalam 5 daerah seimbang dengan nomor 11, 12, 13, 14, dan 15.
Permainan dilakukan dengan memutar anak panah (dengan arah bebas). Kemudian pada saat anak panah berhenti, diamati jumlah nomor semua daerah yang dilewati oleh tanda panah tersebut. Asumsikan bahwa anak panah berhenti secara acak di setiap kemungkinan posisi dan tidak berhenti di ruas garis penyekat antar bagian pada lingkaran tersebut. Seorang pemain dinyatakan sebagai pemenang jika jumlah semua nomor yang dilalui anak panah adalah ganjil. Tentukan peluang pemain tersebut menjadi pemenang. - Sebuah wadah memuat 8 buah bola, empat berwarna merah dan empat berwarna hijau. Dua bola diambil sekaligus secara acak dari wadah. Jika bola yang terambil berwarna merah dan hijau, maka kedua bola tersebut dibuang dan dua bola berwarna buru akan dimasukkan ke dalam wadah. Sedangkan jika kondisi lain yang terjadi, maka bola yang terambil dikembalikan ke wadah. Proses pengambilan ini dilakukan terus-menerus sampai wadah hanya berisi bola berwarna biru saja. Jika $P_{xy}$ menyatakan peluang bahwa banyak bola hijau sebelum suatu pengambilan adalah $x$ dan setelah pengambilan tersebut adalah $y$, tentukan setiap nilai $P_{xy}$ yang mungkin.
- Diketahui $n$ adalah banyak angka 1 yang muncul pada hasil penjumlahan berikut. $$1 + 11 + 111 + ⋯ + \underset{201}{\underbrace{11…11}}$$ Jika $k$ adalah bilangan bulat positif yang merupakan penyelesaian dari persamaan di bawah ini, maka tentukan banyak digit dari $k$. $$\underset{n}{\underbrace{11…1}}\text{ }\underset{n+2}{\underbrace{00…0}}\text{ + }\underset{n}{\underbrace{88…88}}\text{ }0=9(k^2-1)$$
- Diketahui himpunan $A$ dan $B$ dengan
$A = \{a, e, i, o, u, x, y, z\}$
$B = \{−2, −1, 0, 1, 2, 3, 4\}$
Fungsi $f$ dari $A$ ke $B$ disebut fungsi asyik jika memenuhi tiga syarat berikut.
1. Untuk setiap $n \in B$ terdapat $m \in A$ sedemikian sehingga $f(m) = n$.
2. Huruf vokal hanya dipetakan ke bilangan genap.
3. Huruf konsonan hanya dipetakan ke bilangan ganjil.
Berikut ini adalah salah satu contoh fungsi asyik yang disajikan dalam bentuk diagram panah.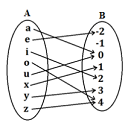
Jika diambil satu fungsi $A$ ke $B$ secara acak, tentukan peluang bahwa yang terambil adalah fungsi asyik. - Suatu fungsi suku banyak berderajat $n$ dapat dinyatakan dalam bentuk
$f(x) = a_nX^n + a_{n−1}X^{n−1} + ⋯ + a_1x + a_0$ dengan $a_n \neq 0$.
Diketahui fungsi suku banyak $T(x)$ memenuhi persamaan
$2T(−c + 2T(x)) = c + x^{16}$ dengan $c$ adalah konstanta.
Tentukan $T(x)$ jika $T(2) = 2021$. - Diketahui $aba$ adalah bilangan tiga digit dengan $a × b$ = 24. Koleksi($n$) adalah barisan bilangan bulat positif yang jumlah dan hasil kali semua sukunya sama dengan $n$. Sebagai ilustrasi, dua contoh Koleksi(12) adalah 1, 1, 1, 1, 2, 6 dan 1, 1, 1, 1, 1, 3, 4. Jika $m$ adalah banyak suku dari Koleksi($aba$), tentukan nilai terbesar $m$ yang mungkin.
- Diketahui daerah segi empat $ABCD$ dengan $AB$ = 2 cm, $BC$ = 8 cm, $CD$ = 6 cm, $DA$ = 7 cm, terbagi menjadi dua daerah segitiga oleh $\overline{AC}$ yang panjangnya 9 cm. Lingkaran dalam kedua segitiga menyinggung $\overline{AC}$ di titik $E$ dan $F$. Jika titik pusat masing-masing lingkaran dalam segitiga adalah $M$ dan $N$, serta luas daerah segitiga $EFM$ adalah $L$ $cm^2$, tentukan nilai maksimum dari $L^2$.
- Dari kubus-kubus yang telah dinomori 1, 2, 3, dst. (setiap sisi suatu kubus memiliki nomor yang sama) akan dipilih kubus-kubus yang dapat dimasukkan ke dalam kelompok A, B, dan C dengan kriteria sebagai berikut.
Kelompok A: kubus dengan nomor 1 (kubus-1).
Kelompok B: kubus yang nomornya hanya memiliki faktor prima, yaitu 3. (contoh: kubus-3, kubus-27).
Kelompok C: kubus yang nomornya dapat dinyatakan sebagai hasil penjumlahan nomor kubus-kubus berbeda yang ada di kelompok A ataupun kelompok B (contoh: kubus-4, kubus-30, kubus-31).
Kubus-kubus dari kelompok A, B, C dapat disusun menjadi priamida dengan banyak kubus di tiap tingkatnya tertentu dan nomornya terurut dari kecil ke besar seperti terlihat pada ilustrasi piramida 2 tingkat dan piramida 3 tingkat berikut.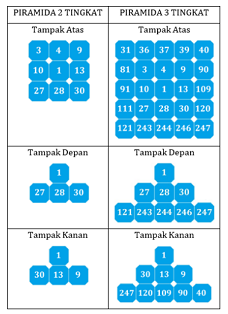
Jika kubus-9 ada di suatu piramida, posisi kubus-9 akan selalu berada dilapisan ke-2 (dihitung dari puncak piramida), baris ke-1, kolom ke-3. Posisi kubus-9 dapat ditulis dengan (2, 1, 3).
Jika kubus dengan nomor terbesar di piramida 100 tingkat diganti oleh kubus-2021 dan kubus-2021 digantikan ke dalam piramida sesua dengan urutan, maka tentunya kubus-2021 akan menggeser posisi kubus-kubus dengan nomor yang lebih besar. Jika setelah diurutkan ternyata kubus-2021 terletak di lapisan ke-m, tentukan nomor kubus yang posisinya ($m, m, m$).
Keranjang Belanja
