- Diketahui dua bilangan bulat positif m dan n dengan $10n − 9m = 7$ dan $m \le 2018$. Bilangan $k = 20 − \frac{18m}{n}$ merupakan suatu pecahan sederhana.
a. Tentukan bilangan pecahan terkecil k yang mungkin
b. Jika penyebut bilangan terkecil k tersebut adalah N, tentukan semua faktor positif dari N.
c. Pada pengambilan satu dari faktor positif dari N, tentukan terambilnya satu faktor kelipatan 4. - Misalkan fungsi $f,g:\mathbb{R}\to \mathbb{R}$ diberikan dalam bentuk grafik berikut.
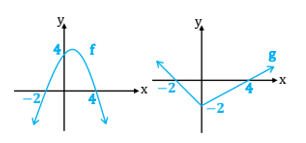
Didefinisikan fungsi $g ∘ f$ dengan $g ∘ f = g(f(x))$ untuk semua $x \in D_f$ dengan $D_f$ adalah daerah asal $f$.
a. Gambarlah grafik fungsi $g ∘ f$
b. Tentukan semua bilangan $x$ agar $−\frac{1}{2}\le (g ∘ f)(x) \le 6$ - Segiempat ABCD memiliki panjang sisi AB = BC = $4\sqrt{3}$ cm dan CD = DA = 4 cm. Semua titik sudut segiempat tersebut terletak pada sebuah lingkaran. Hitunglah luas daerah segiempat ABCD.
- Terdapat bilangan bulat positif x dan y, dengan x < 100 dan y > 9. Diketahui bahwa $y = \frac{p}{777}x$, dengan p berupa bilangan tiga digit yang memiliki digit puluhan angka 5. Tentukan banyaknya nilai y berbeda yang mungkin.
- Bilangan 8 digit berbeda $\overline{abcdefgh}$ disusun dari anggota himpunan $\{1, 2, 3, 4, 5, 6, 7, 8\}$. Bilangan tersebut memenuhi $$a + c + e + g \ge b + d + f + h$$ Tentukan banyaknya bilangan yang mungkin.
- Diberikan bilangan bulat Y yang dengan $$Y=2018+20118+201018+2010018+… … …+201 \underset{100 \text{ digit angka 0}}{\underbrace{000…\text{ }…\text{ }…000}}18$$ Hitunglah jumlah dari semua digit pada bilangan Y tersebut.
- Tiga kelompok garis membagi sebuah bidang menjadi D daerah. Masing-masing garis dalam satu kelompok adalah sejajar. Misalkan x, y, dan z berturut-turut merupakan banyak garis pada kelompok garis ke-1, ke-2, dan ke-3. Jika tidak ada garis pada kelompok 3 yang melalui titik potong dua garis, maka paling sedikit jumlah garis yang dibutuhkan sehingga terdapat lebih dari 2018 daerah adalah ….
- Diketahui limas terpancung ABCD.EFGH dengan ABCD dan EFGH berbentuk persegi yang merupakan dua bidang sejajar. Panjang rusuk persegi ABCD dan EFGH berturut-turut 6a dan 3a serta tinggi limas adalah 3t. Titik M dan N berturut-turut adalah titik potong diagonal ABCD dan EFGH serta MN tegak lurus bidang EFGH. Lukislah limas M.EFGH dan N.ABCD serta hitung volume bangun ruang yang merupakan irisan antara limas N.ABCD dan M.EFGH.
- Perhatikan susunan bilangan asli pada tabel berikut. Posisi dari bilangan tersebut ditentukan dengan nomor baris dan kolom, serta diagonal (yaitu barisan bilangan yang dibaca dari kiri bawah ke kanan atas). Sebagai contoh, posisi bilangan 19 pada baris ke 3, kolom ke-4, dan diagonal ke-6. Sementara posisi dari bilangan 26 adalah pada baris ke-3, kolom ke-5, dan diagonal ke-7.
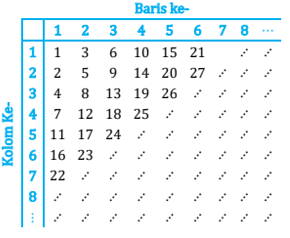
a. Tentukan posisi baris, kolom, dan diagonal dari bilangan 2018
b. Tentukan rata-rata dari barisan bilangan-bilangan yang terletak pada diagonal utama, yaitu barisan bilangan yang dibaca dari ujung kiri atas ke kanan bawah : 1, 5, 13, 25, …. , dengan suku terakhir adalah bilangan terbesar yang kurang dari atau sama dengan 2018. - Diketahui A adalah himpunan bilangan bulat tiga digit yang tidak memuat angaka nol. Didefinisikan bilangan gadang yaitu anggota A yang digitnya berbeda dan penyusunnya bukan bilangan prima serta memberi sisa 5 jika dibagi 7. Jika dipilih secara acak anggota A, berapakah peluang untuk mendapatkan bilangan gadang?
Keranjang Belanja
