- Carilah semua bilangan real $x$ yang memenuhi pertidaksamaan $$\frac{x^2 − 3}{x^2 − 1}+\frac{x^2 + 5}{x^2 + 3}\ge \frac{x^2− 5}{x^2− 3}+\frac{x^2 + 3}{x^2 + 1}$$
- Diketahui $m$ adalah bilangan asli empat angka dengan angka satuan dan ribuan sama. Jika $m$ merupakan bilangan kuadrat, tentukan semua bilangan $m$ yang mungkin.
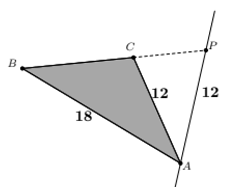
- Pada gambar berikut, $\Delta ABP$ adalah segitiga sama kaki, dengan $AB = BP$ dan titik $C$ pada $BP$. Hitunglah volume dari benda yang diperoleh dari hasil pemutaran $\Delta ABC$ mengelilingi garis $AP$.
- Acara perpisahan suatu kelas dihadiri oleh 10 siswa laki-laki dan 12 siswa perempuan. Wali kelas dari kelas tersebut menyediakan enam hadiah untuk siswa yang dipilih secara acak. Hadiah yang disediakan adalah satu buah tas sekolah, dua buah novel, dan tiga buah kalkulator. Jika total siswa laki-laki yang mendapat hadiah sama banyak dengan total siswa perempuan yang mendapat hadiah, ada berapa banyak susunan yang mungkin dari siswa yang mendapat hadiah?
- Diketahui $S = \{1945, 1946, 1947, · · · , 2016, 2017\}$. Jika $A = \{a, b, c, d, e\}$ himpunan bagian dari $S$ dengan $a + b + c + d + e$ habis dibagi 5, tentukan banyak $A$ yang mungkin.
- Parabola $y = ax^2 + bx, a < 0,$ memiliki titik puncak $C$ dan memotong sumbu-$x$ di titik $A$ dan $B$ yang berbeda. Garis $y = ax$ memotong parabola tersebut di titik berbeda $A$ dan $D$. Jika luas segitiga $ABC$ sama dengan $\left| ab \right|$ kali luas segitiga $ABD$, tentukan nilai $b$ sebagai fungsi dari $a$ tanpa menggunakan tanda nilai mutlak.
Catatan :$\left| ab \right|$ disebut nilai mutlak $x$ dengan $$|x| = \left\{ \begin{array}{cl}
-x, & \text{ jika } x < 0 \\
x, & \text{ jika } x \ge 0
\end{array} \right.$$ - Diketahui $a$ adalah bilangan prima dan $k$ adalah bilangan bulat positif. Jika $\sqrt{k^2 − ak}$ adalah bilangan bulat positif, tentukan nilai $k$ sebagai fungsi dari $a$.
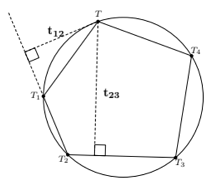
- Terdapat lima titik berbeda, $T_1, T_2, T_3, T_4$ dan $T$ pada sebuah lingkaran $\Omega$. Misalkan $t_{ij}$ adalah jarak dari titik $T$ ke garis $T_iT_j$ atau perpanjangannya. Buktikan bahwa $$\frac{t_{ij}}{t_{jk}}=\frac{TT_{i}}{TT_{k}} \text{ dan } \frac{t_{12}}{t_{24}}=\frac{t_{13}}{t_{34}}$$
- Diberikan barisan bilangan bulat positif 7 angka $a_1, a_2, a_3, · · · , a_{2017}$ dengan $a_1 < a_2 < a_3 < · · · < a_{2017}$. Setiap suku tersebut memiliki angka-angka penyusun dengan urutan tak-naik. Diketahui $a_1 = 1000000$ dan $a_{n+1}$ adalah bilangan terkecil yang mungkin yang lebih besar dari $a_n$. Sebagai contoh diperoleh $a_2 = 1100000$ dan $a_3 = 1110000$. Tentukan $a_{2017}$.
- Pada kilang minyak di daerah Duri, tersedia pompa-1 dan pompa-2. Kedua pompa tersebut digunakan untuk mengisi tangki penampungan dengan volume $V$ . Tangki tersebut dapat diisi penuh menggunakan pompa-1 saja dalam waktu empat jam, atau menggunakan pompa-2 saja dalam waktu enam jam. Mula-mula kedua pompa digunakan secara bersamaan dalam waktu $a$ jam. Kemudian, pengisian dilanjutkan dengan hanya menggunakan pompa-1 selama $b$ jam dan dilanjutkan lagi dengan hanya menggunakan pompa-2 selama $c$ jam. Jika biaya operasional pompa-1 adalah $15(a + b)$ ribu per jam dan biaya operasional pompa-2 adalah $4(a + c)$ ribu per jam, tentukan $b$ dan $c$ agar biaya operasional seluruh pompa adalah minimum (nyatakan $b$ dan $c$ sebagai fungsi dari $a$). Tentukan juga nilai $a$ yang mungkin.
Keranjang Belanja
