- Diketahui $p$ dan $q$ adalah bilangan bulat positif dengan $p-1=\left( k^2-4k-3\right)^2$ dan $q-1=\left( k^2-4k-5\right)^2$. Jika $pq$ adalah bilangan prima, maka nilai yang terbesar yang mungkin bagi $p^2+q^2$ adalah …
A. 10
B. 26
C. 122
D. 1370 - Diberikan suatu fungsi $f\left( x\right)=2025+\frac{x+1}{x}+\frac{x^2+2}{x^2}+\frac{x^3+3}{x^3}+…+\frac{x^{10}+10}{x^{10}}$ untuk sembarang bilangan real.
Carilah nilai $f\left(2 \right)+f\left( 1\right)-f\left( -1\right)-f\left( -2\right)$
A. 0
B. $\frac{565}{256}$
C. $\frac{13365}{256}$
D. 11430 - Jika $$a=\frac{\left( -1 \right)^4\times 4+\left( -1 \right)^3\times 3+\left( -1 \right)^2\times 2+\left( -1 \right)^1\times 1}{2^3}$$ Maka nilai $$\frac{a+\sqrt{a}}{a-\sqrt{a}}$$
A. -3
B. $-\frac{1}{3}$
C. $\frac{1}{3}$
D. 3 - Suatu data terdiri dari 35 bilangan bulat positif. Bilangan terbesar di data tersebut adalah 29 dan mediannya adalah 22. Misalkan rata-rata terkecil yang mungkin dari data-data tersebut adalah $x$ dan rata-rata terbesar yang mungkin adalah $y$. Maka nilai $x+y=$
A. 40,4
B. 37,4
C. 36,4
D. 25,4 - Dalam suatu lingkaran berpusat di $O$ berjari-jari 7, dibuat segitiga $ABC$ dengan titik $A,B,C$ terletak pada keliling lingkaran dan $AC$ sebagai diameter lingkaran dan $\angle ACB=60^o$.
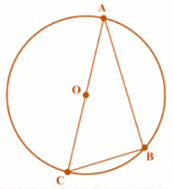
Melalui titik $C$ dan titik tengah $AB$ dibuat garis yang memotong lingkaran di titik $D$. Panjang $CD$ sama dengan …
A. $3\sqrt{7}$
B. $5\sqrt{7}$
C. $6\sqrt{7}$
D. $7\sqrt{7}$ - Suatu perusahaan pembuat baterai mobil listrik sedang melakukan kontrol kualitas terhadap 2000 baterai hasil produksi. Jenis kerusakan pada baterai yang dicek, yaitu kerusakan pelat penutup, kerusakan elektrolit, dan kerusakan terminal. Hasil pengecekan kerusakan dirangkum pada tabel berikut:
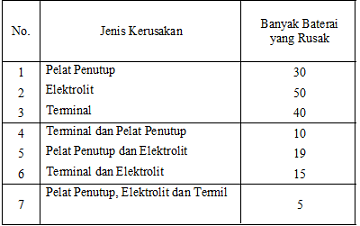
Baterai yang tidak mengalami kerusakan sama sekali dikatakan memenuhi standar. Berdasarkan data tersebut, banyaknya baterai yang memenuhi standar adalah …
A. 1804
B. 1880
C. 1919
D. 1920 - Perhatikan barisan bilangan berikut $$1,2,3,4,6,7,8,9,11,12,13,14,16,17,…$$ Suku-suku barisan tersebut diperoleh dari suku-suku barsian semua bilangan bulat positif dengan menghilangkan kelipatan 5. Suku ke 2025 barisan tersebut adalah …
A. 2430
B. 2530
C. 2531
D. 2532 - Tiga bersaudara Ana, Bona dan Cinta mendapatkan uang saku bulanan mereka dalam bentuk uang pecahan Rp5.000, Rp10.000 dan Rp20.000 dengan pembagian sebagai berikut:
– Ana mendapatkan $x$ lembar Rp5.000, $y$ lembar Rp10.000, serta $z$ lembar Rp20.000.
– Bona mendapatkan $y$ lembar Rp5.000, $z$ lembar Rp10.000, serta $x$ lembar Rp20.000.
– Cinta mendapatkan $z$ lembar Rp5.000, $x$ lembar Rp10.000, serta $y$ lembar Rp20.000.
Diketahui total uang saku ketiganya adalah Rp700.000. Maka pernyataan benar tentang uang saku mereka yang dapat diambil dari informasi tersebut adalah …
A. Ana mendapatkan uang saku sejumlah tepat 20 lembar.
B. Bona mendapatkan uang saku dengan nilai terbesar.
C. Cinta mendapatkan uang saku dengan nilai terkecil.
D. Ana, Bona dan Cinta mendapatkan uang saku lembaran Rp10.000 yang sama banyaknya. - Suatu bidang empat TABC memiliki bidang alas segitiga TBC, TBA dan ABC yang masing-masing saling tegak lurus seperti gambar.
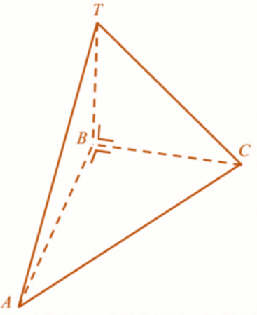
Jika Luas $\Delta TBC$ : Luas $\Delta TBA$ : Luas $\Delta ABC$ = 1 : 2 : 3 dan panjang AC = 10 cm, volume bidang empat TABC sama dengan …
A. $\frac{80}{9}\sqrt{5}$
B. $\frac{80}{3}\sqrt{5}$
C. $80\sqrt{5}$
D. $320\sqrt{5}$ - Suatu objek di titik ($x,y$) hanya dapat bergerak ke titik ($x+1,y$),($x,y+1$) atau ($x+1,y+1$). Banyaknya jalur berbeda yang dapat dilalui objek yang bergerak dari titik (0,0) ke titik (5,5) adalah …
A. 25
B. 252
C. 1683
D. 3125 - Enam bilangan prima yang kurang dari 160 membentuk barisan aritmatika dengan beda lebih dari 1. Jumlah keenam bilangan tersebut adalah …
A. 240
B. 300
C. 492
D. 926 - Banyaknya pasangan terurut bilangan bulat ($x,y$) dengan $-5\le x \le 5$ dan $-5\le y \le 5$, yang memenuhi nilai $10\le x^2+y^2\le 30$ adalah …
A. 10
B. 25
C. 34
D. 68 - Diberikan barisan geometri $80,x,y,z,3125$
Nilai terkecil yang mungkin dari $x-y+z$ adalah …
A. -3120
B. -1950
C. 475
D. 950 - Sebuah buku dibentuk dari beberapa kertas yang ditumpuk dan dilipat ditengah lalu diberi halaman di bagian atas secara terurut seperti pada gambar. Jika salah satu lembar kertas dari buku tersebut diambil, maka jumlah empat nomor halamannnya pada bagian depan dan belakang adalah 122.
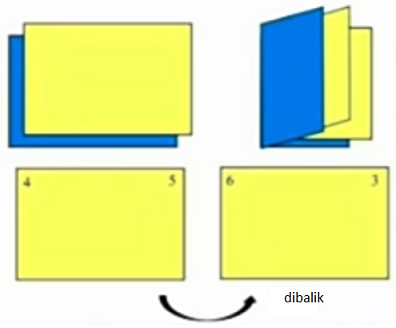
Sebagai contoh keempat nomor halaman untuk bewarna kuning adalah 3 + 4 + 5 + 6 = 18
Banyak kertas yang digunakan untuk menyusun buku tersebut adalah …
A. 60
B. 15
C. 12
D. 10 - Bilangan super ganjil didefinisikan sebagai bilangan bulat positif yang semua digitnya ganjil. Hasil penjumlahan semua bilangan super ganjil yang kurang dari 1000 adalah …
A. 45130
B. 55250
C. 60125
D. 70775 - Dua bilangan bulat positif memiliki jumlah 40 dan kelipatan persekutuan terkecil 48. Faktor persekutuan terbesar dari dua bilangan tersebut adalah …
A. 8
B. 12
C. 16
D. 24 - Segitiga sama sisi $ABC$ dan $DEF$ memiliki panjang sisi yang sama, yaitu 1 cm. Titik $B$ terletak pada sisi $DE$, titik $D$ terletak pada sisi $AB$ dan titik $G$ adalah perpotongan sisi $BC$ dan sisi $DF$.
Jika luas daerah segi empat $ADGC$ sama dengan luas daerah segi empat $BEFC$ dan juga sama dengan luas daerah degitiga $BDG$, maka keliling segi lima $AEFGC$ adalah … cm.
A. $6-\frac{1}{2}\sqrt{2}$
B. $6-\sqrt{2}$
C. $6-\frac{3}{2}\sqrt{2}$
D. $6-3\sqrt{2}$ - Delapan ekor semut ditempatkan pada setiap titik sudut kerangka kubus yang memiliki 8 titik sudut sehingga setiap semut menempati tepat satu titik sudut kubus. Pada saat yang bersamaan masing-masing semut bergerak melawati rangka kubus secara acak menuju salah satu dari tiga titik sudut yang terhubung dengan kecepatan yang sama ke tujuan semua semut berhenti.
Peluang bahwa tidak ada semut yang bertemu dengan semut lain baik di tengah perjalanan maupun di titik sudut tujuan adalah …
A. $\frac{2}{3^8}$
B. $\frac{5}{3^8}$
C. $\frac{4}{3^7}$
D. $\frac{8}{3^7}$ - Suatu segitiga $ABC$ sama kaki dengan $AC=BC$ dan $AB=10$ cm memiliki luas 25 $cm^2$. Titik $D,E$ dan $F$ terletak berturut-turut pada sisi $BC,AC$ dan $AB$ dengan $BD:DC=2:3,CE:EA=2:3$ dan $AF:FB=2:3$. Titik $P,Q$ dan $R$ berturut-turut adalah titik potong garis $AD$ dan $CF$, garis $AD$ dan $BE$ serta garis $BE$ dan $CF$. Perbandingan luas segitiga $PQR$ dan $ABC$ adalah …
A. 1 : 19
B. 2 : 19
C. 3 : 25
D. 1 : 5 - Liam berkesempatan memilih secara acak satu nomor keberuntungan yang terdiri dari 6-digit bilangan dari 0 sampai 9. Ia akan mendapatkan hadiah jika ada setidaknya tiga bilangan ganjil di letak berurutan di nomor keberuntungannya. Peluang Liam mendapatkan hadiah adalah …
A. $\frac{1}{8}$
B. $\frac{3}{16}$
C. $\frac{1}{4}$
D. $\frac{5}{16}$ - Jajar genjang $ABCD$ memiliki keliling 106 cm dengan panjang sisi $AB$ = ($3x+1$)cm dan $BC$ = ($5x-20$)cm. Titik $E$ pada sisi $AB$ sehingga $DE$ tegak lurus $AB$. Titik $F$ dan $H$ pada ruas garis $CE$. Titik $K$ pada sisi $AB$ sehingga $FK$ sejajar $DE$. Titik $G$ berada di dalam segitiga $ECD$ sehingga garis $GF$ tegak lurus $GH$ dan $GF$ sejajar $DE$.
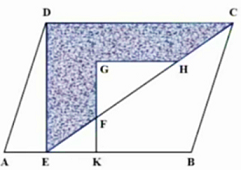
Jika panjang $DE$ = ($3x-7$)cm, $HC=2\times EF$ dan $FK=5$ cm, Luas bangun datar yang diarsir adalah … $cm^2$.
A. 122,5
B. 185
C. 262,5
D. 280 - Oktahedron adalah bangun ruang tiga dimensi dengan 8 bidang sisi datar. Berikut adalah jaring-jaring ruang oktahedron beraturan yang memiliki 8 bidang sisi segitiga sama sisi yang kongruen.
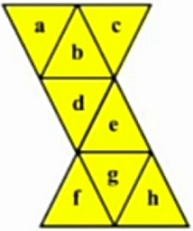
Jika jaring-jaring tersebut dibentuk menjadi oktahedron, maka angka pada setiap bidang sisi sama dengan penjumlahan angka pada semua bidang sisi yang berbagi rusuk dengan bisang sisi tersebut (contoh $B=A+C+D$). Jika $A=-4,C=0,G=-10$ maka nilai $B$ adalah …
A. -10
B. -8
C. 8
D. 10 - Bilangan segi lima ke-$n$ adalah banyaknya titik yang membentuk $n$ segi lima seperti yang diilustrasikan pada gambar berikut.
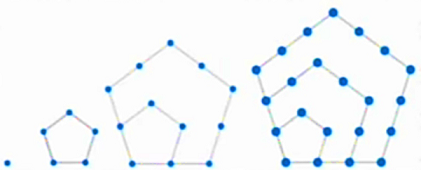
Bilangan segi lima ke-0 adalah 1, bilangan segi lima ke-1 adalah 5, bilangan segi lima ke-2 adalah 12, dan bilangan segi lima ke-3 adalah 22.
Bilangan segi lima yang paling dekat dengan 2025 adalah bilangan segi lima ke- …
A. 30
B. 33
C. 36
D. 39 - Aluna memiliki 9 stiker sebagai berikut

Delapan stiker akan ditempel berjajar dari kiri ke kanan di sampul buku tulisnya. Banyaknya cara ia menempel ke delepan stiker tersebut sedemikian sehingga stiker yang sama tidak bersebelahan dan stiker dengan gambar hati tersenyum terletak di paling kanan adalah …
A. 26
B. 32
C. 35
D. 36 - Berikut ini adalah barisan bilangan bulat positif berurutan dari 1 sampai 10 yang ditulis dengan aturan yang menggunakan hanya huruf $A,B$ dan $C$ saja. $$A,AB,AC,AA,ABB,ABC,ABA,ACB,ACC,ACA$$ Jika aturan tersebut digunakan untuk menuliskan seluruh bilangan bulat positif, maka nilai dari $ABAB$ ditambah $ACAC$ adalah …
A. $ABCCC$
B. $ABCBB$
C. $ABCAC$
D. $ABCAB$
Keranjang Belanja
