- Di samping kolam ikan berbentuk segitiga, dibangun jalan berbentuk $L$ dengan panjang 3 meter dan lebar $x$ meter, seperti yang terlihat pada gambar berikut:
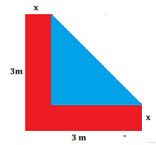
Jika luas segitiga tersebut sama dengan luas daerah yang berbentuk $L$, maka nilai $x$ adalah … meter.
A. $3-\sqrt{6}$B. $2\sqrt{3}-3$
C. $3+\sqrt{6}$
D. $2\sqrt{3}+3$
- A bergerak mendekati B yang berjarak 55 km dengan kecepatan 5 km/jam. Satu jam kemudian, B bergerak menuju A dengan kecepatan $x$ km/jam, dengan $x$ adalah waktu (dalam jam) ketika B berangkat sampai bertemu A. Grafik yang menyatakan hubungan antar waktu $(t)$ yang dibutuhkan A bertemu B dengan jarak (S) A dan B adalah …
A.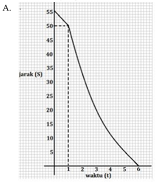
B.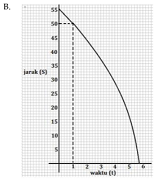
C.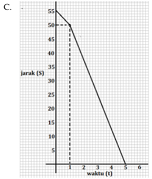
D.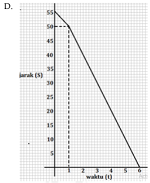
- Misalkan $a, b, c,$ dan $d$ adalah bilangan-bilangan bulat positif yang berbeda sehingga $a + b, a + c,$ dan $a + d$ bilangan ganjil sekaligus bilangan kuadrat. Nilai $a + b + c + d$ terkecil yang mungkin adalah …
A. 33B. 67
C. 81
D. 83
- Diketahui $$x^{2}+\sqrt{xy}+y^{2}=168$$ $$x-\sqrt{xy}+y=10$$ Jumlah semua nilai $x+\sqrt{xy}+y$ yang mungkin adalah …
A. 14B. 27
C. 44
D. 62
- Diketahui sebuah dadu seimbang bersisi 6 semula memiliki mata dadu 2, 3, 4, 5, 6, dan 7. Dadu tersebut dilambungkan satu kali dan diamati hasilnya. Jika yang muncul angka ganjil, maka angka tersebut diganti dengan angka 8. Namun, Jika yang muncul angka genap, maka angka tersebut diganti dengan angka 1, kemudian dadu yang mata dadunya telah diganti tersebut dilambungkan kembali, peluang munculnya mata dadu ganjil adalah …
A. $\frac{1}{3}$B. $\frac{2}{3}$
C. $\frac{1}{2}$
D. 1
- Seorang milliarder sedang membangun hotel. Kamar-kamar hotel tersebut diberi nomor secara berurutan dengan menggunakan bilangan asli mulai dari angka 1. Nomor kamar dibuat dari plat besi seharga Rp8.000 per digit. Sebagai contoh No. 7 perlu biaya Rp8.000 dan No. 11 perlu biaya Rp16.000. Jika hotel tersebut menghasikan biaya sebesar Rp33.416.000 untuk membuat seluruh nomor kamar, maka banyaknya kamar pada hotel tersebut adalah …
A. 1.288B. 1.321
C. 2.700
D. 4.177
- Aima mendapatkan kesempatan makan malam gratis di suatu resto dari tanggal 1 hingga 10 juni 2023. Aima boleh memilih lebih dari satu tanggal kedatangan pada periode tersebut selama bukan tanggal berurutan. Jika Aima berencana datang setidaknya satu kali, maka banyaknya kemungkinan jadwal kedatangan yang dapat dibuat oleh Aima adalah …
A. 45B. 143
C. 144
D. 2025
- Suatu bak penampungan air berbentuk kerucut terbalik (seperti gambar) berisi air dengan volume 1 liter. Jika bak penampungan tersebut ditambahkan air sebanyak 331 mililiter, maka perbandingan antara tinggi air di dalam bak penampungan mula-mula dan setelah ditambahkan air adalah …
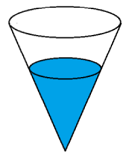
A. 10 : 11B. 11 : 13
C. 331 : 1000
D. 1000 : 1331
- Perhatikan gambar berikut! Di dalam persegi ABCD terdapat dua setengah lingkaran dengan diameter AD dan BC. Ruas garis EF dan GH sejajar AB. Jika EK = 3 cm, LH = 6 cm, dan EG = 9 cm, maka luas daerah persegi ABCD adalah … $cm^{2}$.
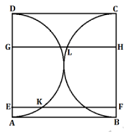
A. 180B. 360
C. 90
D. 150
- Diketahui dua buah segitiga OAB dan OCB dengan O(0, 0), A(4, 0), B(0, 3), dan C(2, 3). Jika segitiga OCB digeser searah sumbu-x sehingga titik O terletak di tengah sisi OA, maka perbandingan antara luas irisan kedua segitiga mula-mula dan luas irisan kedua segitiga setelah segitiga OCB digeser adalah …
A. 3 : 2B. 2 : 1
C. 3 : 1
D. 4 : 1
- Misalkan populasi ikan A semula adalah x dan populasi ikan B semula adalah y. Sekarang, populasi ikan A meningkat 28% dan populasi B berkurang 28%, sehngga rasio populasi ikan A dan B menjadi y/x. Persentase perubahan populasi keseluruhan ikan sekarang dibandingakan total populasi ikan semula adalah …
A. 0%B. 4%
C. 28%
D. 33%
- Diketahui a, b, c, d, e merupakan bilangan bulat positif dengan $a \le b \le c \le d \le e$ dan $a + b + c + d + e = abcde$. Nilai terbesar yang mungkin dari e adalah …
A. 2B. 3
C. 5
D. 7
- Segitiga $ABC$ terletak pada setengah lingkaran berdiameter $AB$ dengan $\angle ABC = 30°$. Titik E terletak pada AB sehingga AB = 4 EB dan EC = 14 cm. Luas segitiga BEC sama dengan … $cm^{2}$.
A. $14\sqrt{3}$B. $16\sqrt{7}$
C. $28\sqrt{3}$
D. $32\sqrt{3}$
- Segitiga ABC siku-siku di A dan ADEC adalah persegi panjang. Titik H terletak pada DE dan lingkaran dengan pusat H menyinggung ketiga sisi segitiga ABC. Jika FG = 2 cm dan EF = 4 cm, maka luas segitiga ABC adalah … $cm^{2}$.
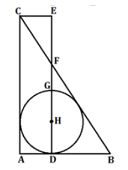
A. 8B. 27
C. 54
D. 108
- Empat orang siswa dipilih mewakili suatu sekolah untk OSK SMP 2023. Peluang ada siswa yang lahir di bulan yang sama adalah …
A. 0,4271B. 0,5729
C. 0,2747
D. 0,4115
- Dua kapal memiliki tempat bersandar (berlabuh) yang sama di suatu pelabuhan. Diketahui bahwa waktu kedatangan kedua kapal saling bebas dan memiliki kemungkinan yang sama untuk bersandar pada suatu hari Minggu (jam 00.00 – 24.00). Jika waktu bersandar kapal pertama adalah 2 jam dan waktu bersandar kapal kedua adalah 4 jam, peluang bahwa satu kapal harus menunggu sampai tempat bersandar dapat digunakan adalah …
A. 67/44B. 1/4
C. 67/288
D. 23/144
- Perhatikan kedua persamaan berikut. $$A=\frac{(p^2+q^2+r^2)^2}{p^2q^2+q^2r^2+r^2p^2}\text{dan }B=\frac{q^2-pr}{p^2+q^2+r^2}$$ Jika $p+q+r=0$, maka nilai $A^2-4B$ adalah …
A. 6
B. 8
C. 12
D. 14 - Diketahui barisan bilangan bulat $x_1,x_2,…,x_{2023}$ yang memenuhi tiga syarat berikut $$x_1+x_3+…+x_{2023}=25-(x_2+x_4+…+x_{2022})$$ $$x_1\text{ }^2+x_3\text{ }^2+…+x_{2023}\text{ }^2=125-(x_2\text{ }^2+x_4\text{ }^2+…+x_{2022}\text{ }^2)$$ $$-2 \le x_i \le 1 \text{ untuk }i=1,2,3,…,2023$$
Nilai terkecil yang mungkin untuk $x_1\text{ }^3+x_3\text{ }^3+…+x_{2023}\text{ }^3$ adalah …
A. -100
B. -71
C. -51
D. -16 - Suatu bilangan prima disebut “prima kanan” jika dapat diperoleh bilangan prima dengan menghilangkan setidaknya satu angka di sebelah kiri. Sebagai contoh. 223 adalah “prima kanan” sebab setelah menghilangkan angka 2 paling kiri, bilangan yang tersisa adalah 23 yang merupakan bilangan prima. Contoh lainnya 127. Dengan menghilangkan 2 angka paling kiri maka angka yang tersisa adalah 7 yang merupakan bilangan prima. Banyaknya bilangan prima antara 10 dan 200 yang merupakan “prima kanan” adalah….
A. 24
B. 26
C. 28
D. 30 - Jika $$M=\frac{1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2023}}{\frac{1}{1\text{ x }2023}+\frac{1}{3\text{ x }2021}+\frac{1}{5\text{ x }2019}+…+\frac{1}{2023\text{ x }1}}$$ maka hasil penjumlahan semua faktor prima dari $M$ adalah …
A. 10
B. 17
C. 30
D. 36 - Jika $(x, y)$ adalah pasangan bilangan bulat positif yang memenuhi $x^2 + 2023x + 2023 = y^2$ dengan $x > y$. Banyaknya $(x, y)$ yang mungkin adalah….
A. 0
B. 2
C. 4
D. Tak hingga - Jika $\binom{n}{k}=\frac{n!}{k!(n-k)!}$, dengan $n!$=1 x 2 x … x $n$ dan $0!$=1, maka nilai darai deret berikut $$\frac{1}{1}\binom{20}{0}+\frac{1}{2}\binom{20}{1}+\frac{1}{3}\binom{20}{2}+\frac{1}{4}\binom{20}{3}+…+\frac{1}{21}\binom{20}{20}$$ adalah …
A. $\frac{(2^{21}-1)}{21}$
B. $\frac{(2^{20}-1)}{21}$
C. $\frac{2^{21}}{21}$
D. $\frac{2^{20}}{21}$ - Banyaknya himpunan bagian dari $\{1, 2, 3, 4, 5, 6, 7, 8, 9\}$ yang berisi 3 bilangan dan memuat tepat dua bilangan ganjil adalah …..
A. 40
B. 84
C. 30
D. 48 - Banyaknya bilangan asli tujuh digit yang disusun dari 0 atau 1 saja serta habis dibagi 6 adalah…
A. 11
B. 17
C. 21
D. 22 - Diketahui suatu konstanta $k > 0$. Garis $l$ dengan persamaan $y = 2kx + 3k^2$ memotong parabola dengan persamaan $y = x^2$ pada titik $P$ di kuadran $I$ dan $Q$ di kuadran II. Jika koordinat $O$(0, 0) dan luas daerah segitiga $POQ$ adalah 48 satuan luas, maka kemiringan garis $l$ adalah….
A. $\frac{2}{3}$
B. 2
C. $\frac{4}{3}$
D. 4
Keranjang Belanja
