OSK SMP 2022

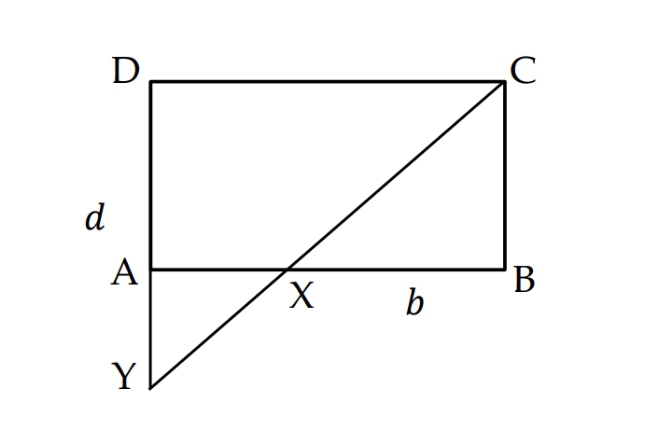
  1. ABCD adalah suatu persegi panjang. Dari titik C ditarik garis lurus yang memotong sisi AB di titik X. Garis CX memotong perpanjangan sisi AD di titik Y. Jika panjang BX adalah b cm, panjang DY adalah d cm, dan luas persegi panjang ABCD adalah L cm2, maka pernyataan yang benar adalah …

    A. $b\text{ x }d=L$
    B. $b\text{ x }d=2L$
    C. $L<b\text{ x }d<2L$
    D. $b\text{ x }d<L$
  2. Diketahui suatu barisan aritmetika $a_{1}, a_{2}, a_{3}, …$ dengan semua sukunya bilangan bulat, $a_{1}$ habis dibagi 3, $a_{2}$ habis dibagi 5, dan $a_{3}$ habis dibagi 7. Jika $a_{1}+a_{2}+a_{3} = 405$ dan $a_{1} > 105$, maka nilai $k$ terkecil sedemikian $a_{k} > 1000$ adalah …
    A. 74
    B. 75
    C. 76
    D. 77

  3. Pada sebuah ujian yang dilaksanakan secara lisan oleh seorang guru digunakan aturan sebagai berikut.

    • Sebanyak 30 pertanyaan berbeda dimasukkan secara berpasangan pada 15 kartu.
    • Seorang siswa mengambil satu kartu secara acak. Jika dia menjawab dengan benar kedua pertanyaan pada kartu yang ditarik, dia dinyatakan lulus.
    • Jika dia menjawab dengan benar hanya satu pertanyaan pada kartu yang ditarik, dia mengambil kartu lain dan guru menentukan yang mana dari dua pertanyaan pada kartu kedua yang harus dijawab. Jika siswa menjawab dengan benar pertanyaan yang ditentukan, siswa tersebut dinyatakan lulus. Pada keadaan lainnya siswa dinyatakan gagal.
    Jika seorang siswa mengetahui jawaban dari 25 pertanyaan dan tidak tahu jawaban yang benar untuk 5 pertanyaan lainnya, peluang siswa tersebut lulus ujian adalah …
    A. $\frac{195}{203}$
    B. $\frac{185}{203}$
    C. $\frac{175}{203}$
    D. $\frac{165}{203}$
  4. SMP Nusantara mengadakan kegiatan menanam pohon yang diikuti oleh sejumlah guru pria dan guru wanita. Sepertiga dari keseluruhan guru tersebut mengajak serta siswa dengan aturan satu guru hanya mengajak satu siswa. Terdapat 159 pohon yang ditanam. Jika satu orang guru pria menanam 13 pohon, satu orang guru wanita menanam 10 pohon, dan 1 orang siswa menanam 6 pohon, maka banyaknya guru wanita yang menanam pohon adalah …
    A. 5
    B. 7
    C. 9
    D. 12

  5. Perhatikan setengah lingkaran pusat O dan diameter AB berikut!

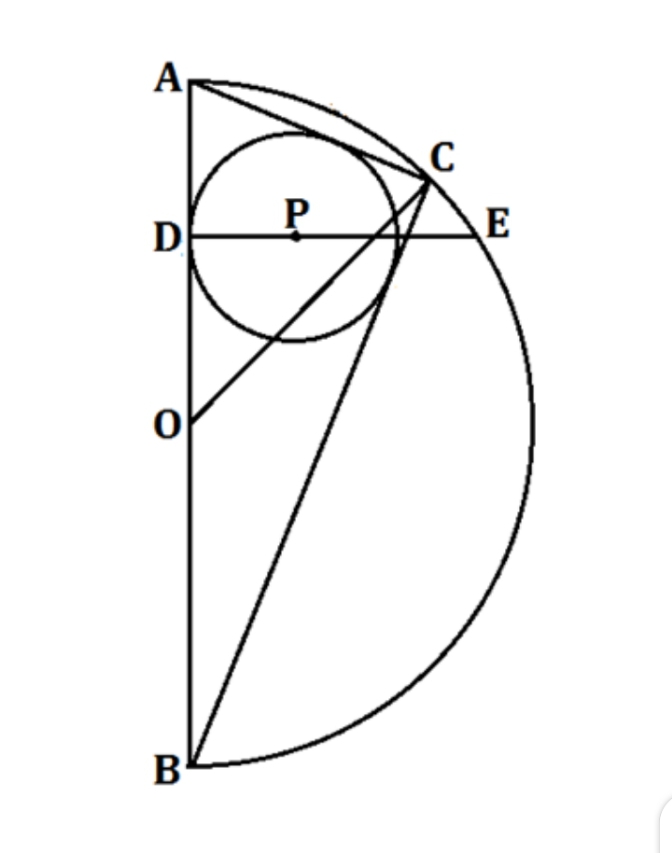    Titik C terletak pada busur AB dan P adalah pusat lingkaran dalam ABC. Titik P dilalui DE yang tegak lurus AO, Jika $DE = 4$ cm, maka luas daerah $\Delta OBC$ adalah … $cm^{2}$.
    A. 2
    B. 4
    C. 8
    D. 16
  6. Tiga puluh koin dengan jari-jari 3,5 cm ditumpuk menjadi 4 tingkat sehingga meyerupai limas tegak segi empat beraturan dengan sisi angka menghadap ke atas. Tingkat pertama (paling bawah) terdiri dari 16 koin, tingkat kedua terdiri dari 9 koin, tingkat ketiga terdiri dari 4 koin dan tingkat keempat terdiri dari 1 koin. Pada setiap tingkat, koin akan disusun menyerupai persegi dengan setiap koin yang berdekatan saling bersinggungan. Jika dilihat dari atas, total luas sisi angka yang tertutup oleh koin lainnya adalah … $cm^{2}$.
    A. 381,5
    B. 444,5
    C. 539
    D. 1155
  7. Diketahui persegi $ABCD$ dengan panjang sisi 12 cm. Titik $P$ terletak pada sisi $CD$ dengan $CP:DP$ = 1 : 2. Persegi ini akan dibentuk menjadi selimut tabung dengan cara mempertemukan sisi AD dengan sisi BC. Jika jarak titik A ke titik P di selimut tabung yang terbentuk adalah $\sqrt{\frac{a+bπ^{2}}{π^{2}}}$ cm, maka $a + b$ = …
    A. 252
    B. 260
    C. 180
    D. 165
  8. Dalam suatu kotak tertutup, terdapat dua buah dadu dengan enam sisi. Dadu pertama memiliki satu sisi bermata 1, satu sisi bermata 2, dua sisi bermata 3, dan dua sisi bermata 5. Sedangkan Dadu keduamemiliki satu sisi bermata 1, satu sisi bermata 2, satu sisi bermata 3, dan tiga sisi bermata 5. Suatu permainan dilakukan dengan mengambil secara acak satu dadu dari dalam kotak, kemudian melemparkan dadu tersebut, mengamati hasilnya, dan memasukkannya kembali ke dalam kotak. Permainan dapat diulang beberapa kali. Andi main dua kali dan mendapatkan hasil amatan mata 1 pada permainan pertama dan mata 5 pada permainan kedua. Peluang bahwa hanya dadu kedua yang terambil pada kedua permainan yang dilakukan Andi adalah …
    A. 0,4
    B. 0,3
    C. 0,2
    D. 0,1
  9. Diketahui $f(x) = x^{2022} − x^{2021}$ dan $g(x) = x^{2020} − 2x^{2019} + 3x^{2018} − 4x^{2017} + ⋯ − 2020x + 2021$.
    Jika $n$ adalah nilai minimum dari $f(x) + g(x)$ untuk $x$ bilangan real, maka nilai $n + 1$ adalah …
    A. 1011
    B. 1012
    C. 2021
    D. 2022
  10. Banyaknya kemungkinan bilangan bulat positif $n$ yang kurang dari 95 dan mengakibatkan $(\sqrt[3]{6})^{200-n}\left( \frac{1}{\sqrt{3}} \right)^{n}$ bilangan bulat adalah …
    A. 14
    B. 15
    C. 16
    D. 17
  11. Doni membeli 3 pasang burung kutilang di pasar dan membawanya dalam 1 wadah besar. Sampai di rumah, burung-burung tersebut akan ditempatkan secara acak ke dalam 3 sangkar berbeda yang masing-masing berisi 2 burung. Peluang setiap burung akan ditempatkan di kandang bersama pasangannya yang sesuai adalah …
    A. $\frac{1}{15}$
    B. $\frac{1}{10}$
    C. $\frac{1}{5}$
    D. $\frac{1}{6}$
  12. Banyaknya bilangan bulat positif yang habis membagi $10^{199}$ dan merupakan kelipatan $10^{111}$ adalah …
    A. 7921
    B. 12544
    C. 32079
    D. 40000
  13. Jika $a, b, c, d$ bilangan-bilangan asli sehingga $$a^{5} = b^{4}, c^{3} = d^{2}, \text{dan } c − a = 19$$ maka nilai dari $d − b$ adalah …
    A. 757
    B. 243
    C. 1000
    D. 81
  14. Diketahui barisan himpunan bilangan dengan pola berikut $$\{1\}, \{2,3\}, \{4,5,6\},…$$
    Himpunan pertama memiliki 1 anggota, yaitu bilangan bulat positif pertama.
    Himpunan berikutnya memiliki 1 anggota lebih banyak dibanding himpunan sebelumnya, dengan anggota adalah bilangan bulat positif pada urutan berikutnya. Jika $M_{n}$ adalah rata-rata dari seluruh anggota himpunan ke-$n$, maka $2M_{2022} − 2M_{2021}$ = …
    A. 2021
    B. 2022
    C. 4043
    D. 4044

  15. Nilai ulangan harian Matematika siswa Kelas VII di SMP Harapan disajikan dalam grafik berikut.

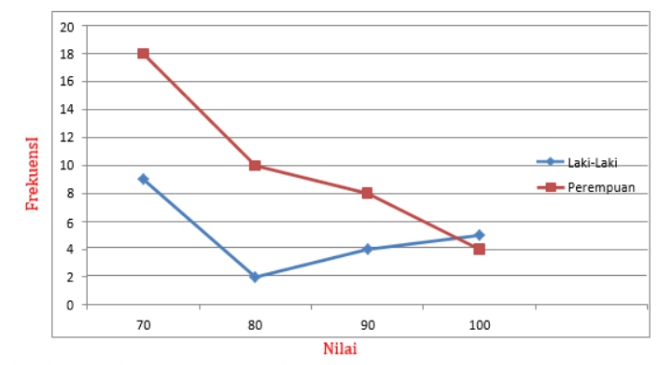    Grafik tersebut memberikan frekuensi nilai kelompok siswa laki-laki (L) dan siswa perempuan (P) secara terpisah. Misalkan RL dan ML, menyatakan rata-rata dan median nilai kelompok siswa laki- laki serta RP dan MP menyatakan rata-rata dan median nilai kelompok siswa perempuan. Di antara pernyataan berikut, pernyataan yang benar adalah …
    A. $M_{P}=M_{L}$
    B. $M_{P}<M_{L}$
    C. $R_{P}=R_{L}$
    D. $R_{P}>R_{L}$
  16. Bilangan “primus” dihasilkan dari bilangan 4 digit $\overline {abcd}$ dengan $b=0$ yang melalui 3 langkah berikut:
    (i) Kurangi $\overline {abcd}$ dengan jumlah semua digitnya
    (ii) Bagilah hasil dari langkah (i) dengan 9
    (iii) Kurangilah bilangan hasil dari langkah (ii) dengan 99 kali digit pertama bilangan hasil dari langkah (ii)
    Di antara bilangan berikut, yang bukan merupakan bilangan “primus” adalah …
    A. 38
    B. 59
    C. 104
    D. 117
  17. Perhatikan persamaan berikut: $$\sqrt{x+2-4\sqrt{x-2}}+\sqrt{x+7-6\sqrt{x-2}}=1$$ Banyaknya bilangan bulat $x$ yang memenuhi persamaan tersebut adalah …
    A. 1
    B. 2
    C. 4
    D. 6

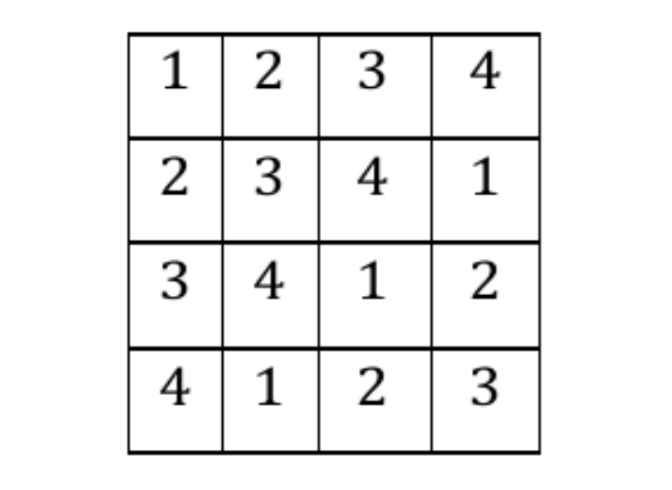
  18. Rio ingin bermain Sudoki pada kotak berukuran 4 x 4. Peraturan permainan Sudoki adalah setiap sel harus diisi dengan salah satu dari angka 1, 2, 3, atau 4 dengan syarat tidak boleh ada angka yang sama dalam pada setiap baris maupun kolom. Berikut diberikan salah satu contoh tampilan akhir permainan Sudoki yang mungkin. Banyak tampilan sudoki yang mungkin adalah …

    A. 50
    B. 576
    C. 432
    D. 676

  19. Perhatikan gambar setengah lingkaran dengan pusat O.

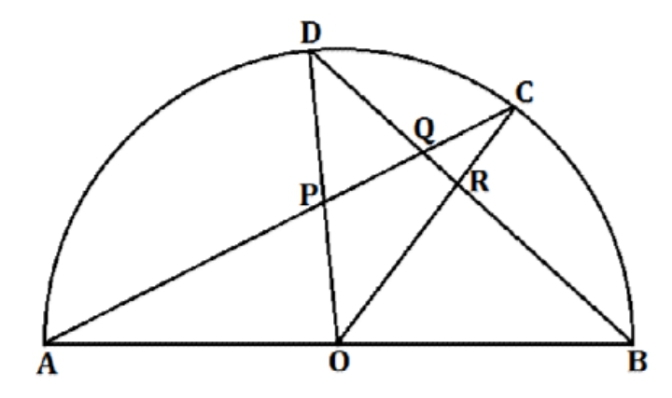    Jika $\angle BOR = 48°$ dan $\angle OPA = 80°$, maka besar $\angle PQR$ = …°.
    A. 92
    B. 104
    C. 118
    D. 125
  20. Urutan kelima bangun datar disebut ideal jika ketiga syarat berikut terpenuhi
    (i) Ada tepat 1 bangun diantara segilima dan segienam
    (ii) Ada lebih dari 1 bangun diantara segitiga dan segi delapan
    (iii) Segiempat tidak disebelah segienam maupun segi delapan
    Banyaknya urutan yang tidak ideal dari kelima bangun datar tersebut adalah …
    A. 1
    B. 2
    C. 118
    D. 119
  21. Jika $a_{1}$ dan $a_{2}$ adalah 2 bilangan bulat positif terkecil berbeda yang memenuhi $a^{9} + 2$ habis dibagi 10 maka nilai dari $a_{1} + a_{2}$ adalah …
    A. 18
    B. 22
    C. 24
    D. 26

  22. Berikut ini adalah sel 3 x 3 yang akan diisi dengan bilangan bulat positif sedemikian sehingga jumlah 3 bilangan dalam setiap baris, kolom, maupun diagonal sama. Jika $n$ adalah nilai terkecil yang mungkin untuk mengisi sel pojok kiri atas, maka jumlah semua bilangan yang berada di keempat sel pojok adalah …

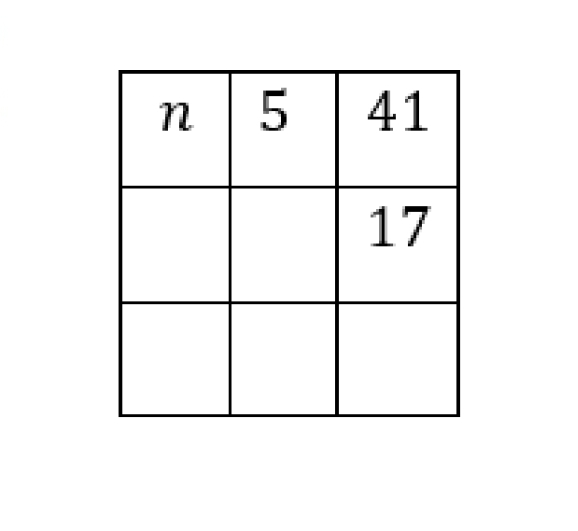    A. 104
    B. 105
    C. 107
    D. 110
  23. Diketahui suatu persegi panjang $ABCD$ dengan titik $P$ dan $Q$ masing-masing berada pada sisi $AB$ dan $CD$ sedemikian sehingga $APCQ$ merupakan belah ketupat. Titik $R$ merupakan titik pusat persegi panjang $ABCD$. Titik $S$ terletak di sisi $CD$ dan $PS$ tegak lurus dengan sisi $CD$. Jika panjang $AB = a$ dan panjang $BC = b$ selisih panjang $RS$ dan $QS$ adalah …
    A. $\frac{a}{b}\sqrt{a^{2}+b^{2}}-\frac{2a^{2}}{b}$
    B. $\frac{b}{2a}\sqrt{a^{2}+b^{2}}-\frac{b^{2}}{a}$
    C. $\frac{b}{a}\sqrt{a^{2}+b^{2}}-\frac{2a^{2}}{b}$
    D. $\frac{2a}{b}\sqrt{a^{2}+b^{2}}-\frac{a}{b^{2}}$
  24. Perhatikan persamaan berikut. $$x^{2023}-x^{2021}-x^{2019}-…-x^{3}=2x$$ Jumlah dari kuadrat akar-akar real persamaan tersebut adalah …
    A. 0
    B. 4
    C. 6
    D. 9
  25. Diketahui himpunan A sebagai berikut. $$\left\{ \frac{(n-2)^{2}+2}{m},\frac{(n-2)^{3}+2}{m},\frac{(n-2)^{4}+2}{m},… \right\}$$ Semua anggota A adalah bilagan bulat positif. Jika $n$ adalah kelipatan dari $m$, maka jumlah semua nilai $m$ yang mungkin untuk $n=2022$ adalah …
    A. 3
    B. 6
    C. 12
    D. 28
Keranjang Belanja
Scroll to Top