OSK SMP 2012

  1. Pernyataan yang benar di antara pernyatan-pernyataan berikut adalah …
    A. $\left\{ \phi \right\}\in \phi$
    B. $\left\{ \phi \right\}\subseteq \phi$
    C. $\phi \subseteq \phi$
    D. $\left\{ a,b \right\}\in \{ a,b,\{ \{ a,b \} \} \}$
    E. $\{ a,\phi \}\subseteq \{ a,\{ a,\phi \} \}$
  2. Diketahui persegi $ABCD$. Jika titik $E$ terletak pada $BC$ dan titik $F$ terletak pada $CD$ sehingga $AE$ dan $AF$ membagi persegi $ABCD$ menjadi 3 daerah yang luasnya sama, maka perbandingan luas segitiga $AEF$ terhadap luas persegi $ABCD$ adalah …
    A. 4/18
    B. 5/18
    C. 6/18
    D. 7/18
    E. 8/18
  3. Jika kedua akar persamaan $p^{2}x^{2}-4px+1=0$ bernilai negatif, maka nilai $p$ adalah …
    A. $p<0$
    B. $p<\sqrt{3}-\frac{1}{2}$
    C. $p<\sqrt{3}+\frac{1}{2}$
    D. $p<\sqrt{3}$
    E. $p<2-\sqrt{3}$
  4. Jika $f(x)=3x+1, g(x)=1-2x$, dan $f(g(a))=28$, maka nilai $a$ adalah …
    A. -7
    B. -4
    C. 4
    D. 7
    E. 13,5
  5. Suatu $byte$ didefinisikan sebagai susunan angka yang terdiri dari 8 angka (digit), yaitu 0 atau 1. Contoh $byte : 01110111$. Banyak jenis $byte$ yang memuat angka 1 tepat sebanyak 5 adalah …
    A. 30
    B. 45
    C. 56
    D. 62
    E. 66

  6. Perhatikan pola bilangan berikut. Bilangan 2012 akan terletak dibawah huruf …

    A. Q
    B. R
    C. S
    D. T
    E. U
  7. Jika $m$ dan $n$ adalah bilangan bulat positif sehingga $m^{2}+2m+3n=33$, maka banyak bilangan $n$ yang memenuhi adalah …
    A. 7
    B. 6
    C. 5
    D. 4
    E. 3
  8. Enam pipa besar dapat mengeringkan sebuah kolam dalam waktu 5 jam, sedangkan delapan pipa kecil dapat mengeringkan kolam tersebut dalam waktu 10 jam. Waktu yang diperlukan untuk mengeringkan kolam tersebut apabila menggunakan 3 pipa besar dan 5 pipa kecil adalah … jam
    A. 60/13
    B. 80/13
    C. 90/13
    D. 8
    E. 9
  9. Lima orang guru akan ditempatkan pada tiga sekolah yang berbeda, 2 orang di sekolah pertama, 2 orang disekolah kedua dan 1 orang di sekolah ketiga. Banyak cara menempatkan kelima orang guru tersebut adalah …
    A. 40
    B. 30
    C. 20
    D. 10
    E. 4

  10. Diketahui persegi panjang $PQRS$. Panjang $PV=QT=PS=6$. Titik $U$ adalah perpotongan antara garis $SV$ dan $RT$ (seperti gambar dibawah). Jika $PQ=10$ maka luas segiempat $PTUS$ adalah …

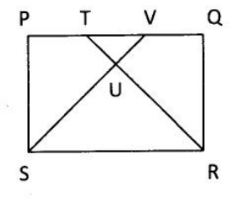    A. 15
    B. 17
    C. 19
    D. 21
    E. 23
  11. Empat bola bernomor 1,2,3 dan 4 diletakkkan dalam sebuah kotak. Sebuah bola diambil secara acak dari kotak tersebut. Nomor yang muncul dicatat, kemudian bola dikembalikkan ke kotak semula. Jika proses pengambilan bola dilakukan sampai tiga kali dengan cara yang serupa, maka peluang nomor bola yang terambil berjumlah 5 adalah …
    A. 5/256
    B. 5/64
    C. 1/16
    D. 3/32
    E. 3/16
  12. Suatu antrian pembelian tiket masuk pertandingan sepak bola terdiri dari 2012 orang. Jika diantara 2 pria paling sedikit terdapat 3 wanita, maka banyak pria pada antrian tersebut paling banyak adalah …
    A. 501
    B. 502
    C. 503
    D. 504
    E. 505
  13. Diketahui $abc$ dan $def$ adalah bilangan yang terdiri dari 3 angka (digit) sehingga $abc+def=1000$ Jika $a,b,c,d,e$ atau $f$ tidak satupun yang sama dengan 0, maka nilai $a+b+c+d$ adalah …
    A. 25
    B. 26
    C. 27
    D. 28
    E. 29
  14. Suatu tes matematika terdiri dari 5 soal pilihan ganda dengan lima pilihan dan hanya ada satu pilihan yang benar. Jika Mulan menjawab soal secara menerka (secara acak atau asal-asalan), maka peluang tepat dua soal dijawab dengan benar adalah …
    A. 32/725
    B. 32/625
    C. 64/725
    D. 64/625
    E. 128/625
  15. Untuk setiap bilangan bulat $x$ didefinisikan fungsi $f$ dengan $f(x)$ adalah banyak angka (digit) dari bilangan $x$. Contoh : $f(125)=3$ dan $f(2012)=4$. Nilai $f(2^{2012})+f(5^{2012})$ adalah …
    A. 2013
    B. 2014
    C. 2015
    D. 2016
    E. 2025
  16. Dalam sebuah karung terdapat 60 kaos bernomor 11,12,13,…40. Ada 2 kaos untuk setiap nomor (nomor 11 ada 2 kaos, nomor 12 ada 2 kaos dan seterusnya). Jika diambil 2 kaos secara acak, maka peluang yang terambil adalah kaos yang bernomor sama adalah …
    A. 1/59
    B. 2/35
    C. 2/33
    D. 2/31
    E. 2/29
  17. Sehabis belanja, Ratina membawa pulang uang kembalian berupa 8 koin (uang receh), yang terdiri dari ratusan, lima-ratusan dan ribuan. Total nilai uang kembalian adalah tiga ribu rupiah. Sayangnya, dalam perjalanan pulang salah satu uang koin jatuh (hilang). Jika peluang kehilangan untuk satu ratusan, satu lima-ratusan, dan satu ribuan adalah sama, maka peluang kehilangan satu koin lima-ratusan adalah …
    A. 1/8
    B. 2/8
    C. 3/8
    D. 4/8
    E. 5/8
  18. Jika 2,3,5,6,7,10,11,… adalah barisan yang terdiri dari semua bilangan asli yang bukan bilangan kuadrat dan bukan bilangan pangkat tiga, maka bilangan 270 adalah suku ke …
    A. 247
    B. 248
    C. 249
    D. 250
    E. 251
  19. Suatu balok dengan volume 240 satuan mempunyai panjang $a,$ lebar $b$, dan tinggi $c$ ($a,b,c$ adalah bilangan asli). Jika $a+b+c=19$ dan $a>b>c>3$, maka luas permukaan balok yang sisinya mempunyai rusuk $b$ dan $c$ adalah …
    A. 64
    B. 60
    C. 48
    D. 40
    E. 30

  20. Perhatikan gambar dibawah ini. Jika lingkaran besar berjari-jari 4 dan lingkaran kecil berjari-jari 2, serta luas daerah yang diarsir adalah $\frac{5}{12}$ luas lingkaran besar, maka besar $\angle RPQ$ adalah …

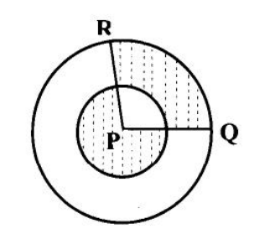    A. $60\circ$
    B. $90\circ$
    C. $120\circ$
    D. $135\circ$
    E. $150\circ$
 
ISIAN SINGKAT
  1. Diketahui 2012 bilangan bulat positif berurutan. Jika setiap bilangan tersebut dibagi 5, kemudian sisa-sisa pembagiannya dijumlahkan, maka hasil penjumlahan sisa-sisanya adalah …
  2. Jika $a=b+2,a^{2}=b^{2}+6$ dan $3(a+b)^{2}c+3(a+b)c^{2}+c^{3}=10+(a+b)^{3}$, maka nilai $c$ adalah …
  3. Jika segitiga $ABC$ siku-siku di $B, AB=6,AC=10$ dan $AD$ adalah garis bagi sudut $BAC$, maka panjang $AD$ adalah …
  4. Semua nilai $x$ yang memenuhi persamaan $\sqrt{(6x-2)}-\sqrt{(4x-3)}=1$ adalah …
  5. Jika rata-rata 1000 bilangan ganjil positif berurutan adalah 2012, maka bilangan terkecil dari bilangan-bilangan tersebut adalah …
  6. Jalan Majapahit sejajar dengan jalur kereta api yang membentang lurus. Anton menampung bus OSN di jalan Majapahit dengan kecepatan konstan (tetap) 40km/jam. Dari arah berlawanan, bus yang ditumpangi Anton berpapasan dengan kereta api barang yang bergerak dengan kecepatan konstan 20 km/jam. Anton mencatat bahwa bus dan kereta api berpapasan selama seperempat menit terhitung mulai dari lokomotif (bagian paling depan) sampai bagian paling belakang. Panjang kereta api tersebut adalah … meter.
  7. Banyak himpunan bagian dari himpunan $\{ a,b,c,d,e,f \}$ yang memuat sedikitnya satu huruf vokal adalah …
  8. Empat titik ditempatkan pada lingkaran berjari-jari 1/2 satuan. Jika keempat titik tersebut dihubungkan sehingga membentuk persegi panjang, maka luas terbesar (maksimum) yang mungkin bagi persegi panjang tersebut adalah …
  9. Kubus $ABCD.EFGH$ mempunyai panjang rusuk 2 cm. Jika titik $T$ adalah titik potong diagonal bidang $BCGF$, titik $P$ adalah titik tengah rusuk $AB$ dan titik $Q$ adalah titik tengah rusuk $DC$ maka jarak antara titik $T$ dengan bidang $PQHE$ adalah … cm
  10. Misalkan $ab$ adalah bilangan terdiri dari dua angka. Jika bilangan itu ditambah 45, maka diperoleh bilangan $ba$. Pada bilangan $ab$, jika di antara $a$ dan $b$ disisipkan angka 0, maka diperoleh bilangan yang nilainya $7\frac{2}{3}$ kali bilangan $ab$. Bilangan $ab$ tersebut adalah …
Keranjang Belanja
Scroll to Top