OSP SD 2011

  1. There are young brothers. The younger brother is between 30 and 40 years of age and other is between 40 and 50 years of age. The product of their ages is a perfect cube. The sum of their ages is ……
  2. if A – B = 2009, B – C = – 2010 dan C – D = 2011, then the value of $\frac{A−D}{(A−C)(B−D)}$ is …..
  3. Perhatikan gambar berikut!
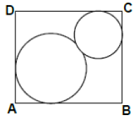    Dua lingkaran dengan jari-jari 17 dan 9 bersinggungan. Jika AB = 50, maka luas persegi panjang ABCD adalah …..
  4. For how many positive value of n are both $\frac{n}{3}$ and $3n$ four-digit integer?
  5. What is the largest integer less than 2011 that has a remainder of 5 when divided by 7, a remainder of 10 when divided 11 and a remainder of 10 when divided 13 ?
  6. How many ounces of pure water must be added to 30 ounces of a 30% solution of acid to yield a solution that is 20% acid ?
  7. Three squares with sides of length two, four and six units, respectively, are arranged side by side.

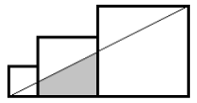
    What is the area of the shaded guadrilateral ?
  8. Jika bilangan positif $x$ ditambahkan pada pembilang dan penyebut dari pecahan $\frac{2011}{8}$, maka pecahan tersebut menjadi bilangan bulat. Nilai $x$ yang memenuhi adalah …..
  9. Bilangan 8 mempunyai dua sifat :
    *). Jika bilangan itu ditambah 1, diperoleh bilangan kuadrat sempurna, yaitu 9 = 3 x 3
    *). Setengah dari bilangan itu adalah 4 yang juga bilangan kuadrat sempurna, yaitu 4 = 2 x 2.
    Bilangan berikutnya yang terkecil dan mempunyai sifat seperti itu adalah …..
  10. $A, B$, dan $C$ adalah bilangan-bilangan prima berbeda. Jika $A$ × $B$ × $C$ adalah bilangan genap dan $A$ × $B$ × $C > 100$, maka nilai terkecil dari $A + B + C$ adalah …..
  11. Adi dan Agung masing-masing memiliki 12 bola dan 15 bola. Jika $a$ kali banyak bola Adi sama dengan $b$ kali banyak bola Agung, maka nilai terbesar dari $b − a$ adalah …..
  12. Nilai paling sederhana dari $$\left[ \frac{3}{1+\frac{1}{3}} \right]\times\left[ \frac{4}{2+\frac{1}{4}} \right]\times\left[ \frac{5}{3+\frac{1}{5}} \right]\times …\times\left[ \frac{59}{57+\frac{1}{59}} \right]\times\left[ \frac{60}{58+\frac{1}{60}} \right]$$
  13. Ada tujuh bar berukuran 3 cm $\times$ 1 cm di dalam kotak berukuran 5 cm $\times$ 5 cm, seperti tampak pada gambar berikut.
    Minimal beberapa bar yang mungkin harus digeser agar ada ruang kosong untuk satu lagi bar di dalam kotak tersebut?
  14. Jumlah dari 2011 bilangan pertama pada pola barisan berikut :
    1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, … adalah …..
  15. Sepuluh anak lahir pada tanggal yang sama pada tahun yang berurutan. Jika jumlah umur 4 anak termuda adalah 26, maka jumlah umur dua anak tertua adalah ….
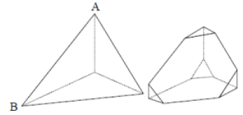
  16. A solid triangular pyramid has six edges such as AB. Each corner is cut off. (see new figure) How many edges will the new figure have?
  17. Perhatikan gambar berikut.
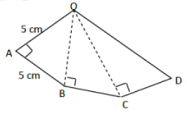    Jika $\angle OAB = \angle OBC = \angle OCD = 90\circ$ dan panjang $AB=BC=CD$, maka jumlah panjang dari $OB, OC$, dan $OD$ adalah ….
  18. Logo dari suatu organisasi seperti tampak pada gambar berikut.
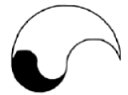    Bila logo tersebut seluruhnya tersusun dari busur setengah lingkaran dengan jari-jari 1 cm, 2 cm, 4 cm atau 8 cm. Luas dari bagian dari logo yang diarsir adalah ……
  19. Pada gambar ABCD adalah persegipanjang, PQRS adalah persegi. Bila daerah diarsir adalah setengah dari luas persegi panjang ABCD, maka panjang PX adalah …..
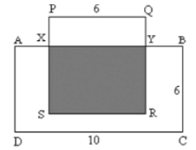
  20. Lengkapilah kotak-kotak di bawah ini dengan menggunakan angka-angka 1, 2, 3, dan 4, sehingga tidak ada angka yang sama dalam satu kolom, baris dan diagonalnya!
  21. Hitunglah:
    $\left( \frac{3-2}{2\text{ x }3} \right)+\left( \frac{4+3}{3\text{ x }4} \right)+\left( \frac{5-4}{4\text{ x }5} \right)+\left( \frac{6+5}{5\text{ x }6} \right)+\left( \frac{7-6}{6\text{ x }7} \right)+\left( \frac{8+7}{7\text{ x }8} \right)+\left( \frac{9-8}{8\text{ x }9} \right)$ = ⋯
  22. Perhatikan gambar berikut ini.
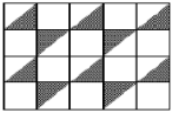    Perbandingan daerah berwarna gelap dengan daerah yang terang adalah …..
  23. Harga tiket kereta api Surabaya-Bandung kelas bisnis Rp150.000,00 untuk orang dewasa, dan anak-anak 50% dari tiket dewasa. Jika pada suatu hari penumpang di suatu gerbong ada 60 orang dan uang yang terkumpul adalah Rp6.000.000,00, maka banyak orang dewasa yang ada dalam gerbong itu adalah ….
  24. Di antara 5 bilangan berikut: $A =\frac{7}{8}, B =\frac{66}{77}, C =\frac{555}{666}, D =\frac{4444}{5555}, E =\frac{33333}{44444}$ bilangan manakah yang terkecil?
  25. Diketahui $x =\frac{1}{1^5} +\frac{1}{2^5} +\frac{1}{3^5} +\frac{1}{4^5} +\frac{1}{5^5} + ⋯$
    dan $y =\frac{1}{1^5} +\frac{1}{3^5} +\frac{1}{5^5} +\frac{1}{7^5} +\frac{1}{9^5} + ⋯$
    Nilai $\frac{y}{x}$ = ⋯
 
URAIAN
  1. The rectangle below consist of 6 unit squares formed by using 17 identical sticks. Each side of a unit square is formed by one stick. The greatest number of unit squares in a rectangle that can be formed by using exactly 500 identical sticks are …..?
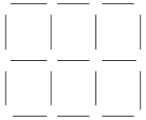
  2. The perimeter of figure below is 304. Find the area ……
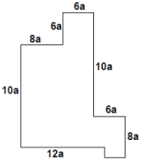
  3. Nurul menjumlahkan $n$ bilangan asli pertama. Pada saat menjumlahkan bilangan-bilangan tersebut, dia membuat kesalahan dengan menghitung sebuah bilangan dua kali sehingga diperoleh hasil 2011. Tentukan bilangan yang dihitung dua kali tersebut.
  4. Antok menulis 11 bilangan bulat positif berurutan di papan tulis. Sebuah bilangan dihapus dan ternyata jumlah bilangan-bilangan yang tersisa adalah 2011. Tentukan bilangan yang dihapus.
  5. Suatu bilangan bulat positif dikatakan bilangan cantik jika bilangan tersebut habis dibagi jumlah angka-angka pembentuknya. Contoh : bilangan 1729 adalah bilangan cantik, sebab $\frac{1729}{1+7+2+9}= 91$ , yaitu 91 bilangan bulat. Tentukan bilangan cantik terkecil dan kelipatan 13.
  6. Nilai $x$ yang memenuhi jumlah berikut $$\frac{x}{11\text{ × }13}+\frac{x}{13\text{ × }15}+\frac{x}{15\text{ × }17}+ ⋯ +\frac{x}{2009\text{ × }2011}=\frac{11}{2011}$$ adalah ….
  7. Now many centimeters are in the diameter of the largest circle ?
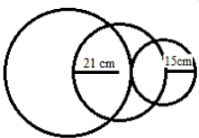
  8. Tiga lingkaran identic dengan jari-jari 6 cm saling bersinggungan satu sama lain. Persegi panjang ABCD dibentuk mengikuti aturan bahwa garis AB menyinggung dua lingkaran, sedangkan sisi-sisi yang lainnya hanya menyentuh satu lingkaran. Hitunglah luas persegi panjang ABCD ?
  9. Jika $ab = a + b$ maka dikatakan bahwa $b$ adalah “sumprod partner” of $a$ . Tentukan sumprod partner dari 2.
  10. Barisan bilangan terdiri dari tujuh bilangan bulat berturut-turut. Bila diketahui jumlah dari tiga bilangan terkecil adalah 33, berapa jumlah dari tiga bilangan terbesar ?
  11. Perhatikan bentuk factorial berikut ini :
       3! = 1.2.3
       4! = 1.2.3.4
       5! = 1.2.3.4.5
    Gunakan fakta di atas untuk menyederhanakan bentuk $\frac{10!−9!}{10!+9!}$
  12. Perhatikan gambar berikut ini :
    Misal AB : BC = 2 : 3, dan BC : CD = 1 : 3. Tentukan CD bila diketahui pula bahwa panjang AD adalah 42 cm.
  13. Misalkan P dan Q berturut-turut menyatakan bilangan terbesar dan bilangan terkecil di antara bilangan 5-angka yang jumlah kelima angkanya adalah 9. Berapakah faktor prima terbesar dari P dan Q?
  14. Tentukan semua bilangan asli 9 angka yang memenuhi sifat-sifat berikut:
    a). Masing-masing angka 1, 2, …, 9 muncul tepat satu kali.
    b). Jika 6 angka terakhir dibuang, maka terbentuk bilangan yang habis dibagi 3 dan memiliki tepat 3 faktor prima.
    c). Jika 6 angka pertama dibuang, maka terbentuk bilangan yang nilainya adalah dua kali lipat suatu bilangan kuadrat yang habis dibagi 3.
    d). Jika 3 angka pertama dan 3 angka terakhir dibuang, maka terbentuk bilangan ganjil yang habis dibagi 9.
    Petunjuk: Bilangan 60 = $2^2$.3.5 memiliki tepat 3 faktor prima.
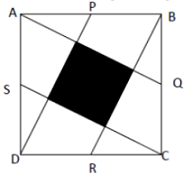
  15. Pada gambar berikut, ABCD adalah persegi. P, Q, R, dan S adalah titik tengah dari AB, BC, CD dan DA berurutan. Tentukan perbandingan dari daerah yang diarsir dan tidak diarsir ?
Keranjang Belanja
Scroll to Top