- Banyak pasangan bilangan prima antara 1 – 50 yang jumlahnya 60 adalah …
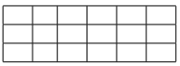
- Luas daerah yang diarsir pada gambar di bawah ini adalah ….
- Jika $a \bigotimes b = \frac{a×b}{a+b}$ maka $(6 \bigotimes 3) \bigotimes (−4)$ =….
- Vida mengumpulkan data tentang rasa es krim kesukaan teman-teman sekelasnya. Hasilnya ditampilkan seperti berikut:
 Persentase banyak teman Vida yang menyukai es krim coklat atau durian adalah….
Persentase banyak teman Vida yang menyukai es krim coklat atau durian adalah…. - Jika 15% dari $\frac{4}{5}$ uang Rani adalah Rp45.000,00, maka $\frac{5}{6}$ uang Rani adalah ….
- Banyak digit hasil operasi bilangan $32^{17}$ × $5^{80}$ adalah ….
- Banyak siswa kelas V-A adalah 30 orang. Mereka akan mengikuti Lomba Permainan Tradisional berkelompok. Tiap kelas boleh mengirimkan lebih dari satu kelompok untuk setiap jenis permainan tetapi setiap siswa hanya boleh mengikuti satu jenis permainan. Banyak anggota kelompok yang dibutuhkan untuk setiap jenis permainan dapat dilihat pada keterangan berikut:
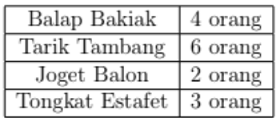 Jika semua jenis permainan diikuti oleh siswa kelas V-A, maka banyak kelompok yang dapat diusulkan kelas V-A paling sedikit adalah … kelompok.
Jika semua jenis permainan diikuti oleh siswa kelas V-A, maka banyak kelompok yang dapat diusulkan kelas V-A paling sedikit adalah … kelompok. - Bilangan Asli berurutan diletakkan mengikuti pola seperti pada tabel berikut.
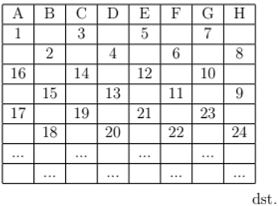
Bilangan 2016 terletak pada kolom (huruf) …. - Diberikan tiga bilangan bulat positif $a, b$ dan $c$ sedemikian sehingga $a : b = b : c = c : a$. Nilai dari $\frac{(150 × a) + (200 × b) + (250 × c)}{a + (3 × b) − (2 × c)}$ adalah ….
- Rata-rata delapan bilangan adalah 15. Jika delapan bilangan tersebut ditambah dengan bilangan kesembilan dan kesepuluh, maka rata-ratanyamenjadi 60. Jika delapan bilangan tersebut hanya ditambah dengan bilangan kesembilan, maka rata-ratanya menjadi 30. Selisih bilangan kesembilan dan kesepuluh adalah ….
- The sum of three numbers $x, y$ and $z$ is 180. If sum of $x$ and $y$ is 130, sum of $x$ and $z$ is 110 then $y + z – x$ equal to ….
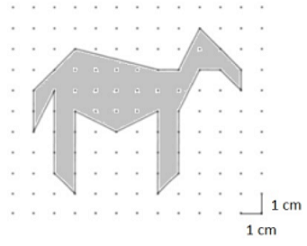
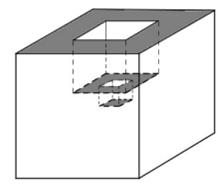
- Diketahui sebuah kubus dengan panjang rusuk $a$ satuan panjang. Jika kubus itu dilubangi sedemikian rupa dengan lubang berbentuk susunan dua kubus yang panjang rusuknya masing-masing setengah satuan panjang rusuk-rusuk kubus sebelumnya, maka akan dihasilkan bentuk bangun ruang seperti di bawah ini. Hitunglah luas permukaan bangun ruang tersebut.
- Sembilan puluh kelereng dimasukkan ke dalam empat kotak. Perbandingan isi kelereng di dalam kotak I, II dan III adalah 2:3:4. Jika isi kotak IV paling banyak di antara semua kotak, maka banyak kelereng minimal pada kotak IV adalah ….
- If ABCD is a square and $\measuredangle APB : \measuredangle CQR = 12 : 21$, then $\measuredangle PBC$ is … $\circ$.

- Andika memiliki lima kartu yang masing-masing bertuliskan bilangan satu digit $a, b, c, d$ dan $e$. Andika mengambil dua kartu secara acak, kemudian mencatat selisih dari kedua bilangan yang tertulis di kartu tersebut. Beberapa hasil operasi bilangan yang muncul pada catatan Andika adalah 1, 2, 4, 6, 7. Nilai terbesar yang mungkin dari $a + b + c + d + e$ adalah ….
- Baharuddin mempunyai koleksi kerajinan tangan yang berasal dari beberapa provinsi seperti ditampilkan pada tabel berikut:
 Kerajinan dari jenis bahan apa yang dimiliki Baharuddin yang persentase koleksi dari Kalimantan lebih besar dibandingkan Sulawesi?
Kerajinan dari jenis bahan apa yang dimiliki Baharuddin yang persentase koleksi dari Kalimantan lebih besar dibandingkan Sulawesi? - Bilangan 2016 dapat ditulis sebagai jumlah dari bilangan asli berurutan (contoh untuk jumlah tiga bilangan : 2016 = 671 + 672 + 673). Berapa cara untuk menuliskannya, bila banyak bilangan yang dijumlahkan empat bilangan atau lebih?
- Persegi panjang berukuran 3 cm × 2 cm dapat ditutup oleh persegi panjang 2 cm × 1 cm atau 1 cm × 2 cm dengan berbagai cara seperti tampak pada gambar di bawah ini.
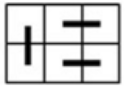 Berapa banyak cara bangun berikut dapat ditutup dengan persegi panjang 2 cm × 1 cm atau 1 cm × 2 cm?
Berapa banyak cara bangun berikut dapat ditutup dengan persegi panjang 2 cm × 1 cm atau 1 cm × 2 cm?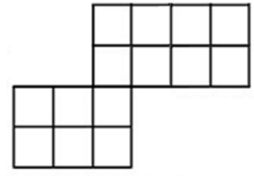
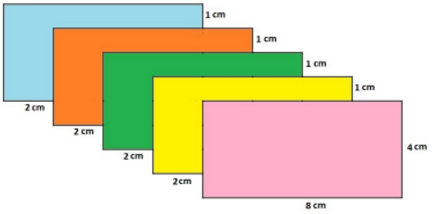
- Terdapat lima kartu berbentuk persegi panjang berukuran 8 cm × 4 cm. Kartu-kartu tersebut kemudian disusun bertumpuk seperti terlihat pada gambar di bawah ini. Berapa luas daerah tumpukan kartu yang tampak?
- Diketahui lima pecahan $\frac{1}{3},\frac{1}{6},\frac{1}{9},\frac{1}{12}$ dan $\frac{1}{15}$ . Empat dari lima pecahan tersebut dilambangkan dengan huruf $a, b, c$ dan $d$. Jika $a + b + c = \frac{7}{12}$ dan $c$ × $d$ = $\frac{1}{45}$ maka nilai $d$ = ….
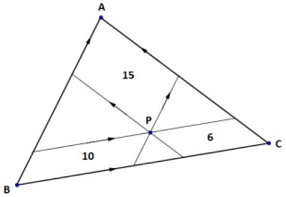
- Melalui titik $P$ di dalam segitiga $ABC$ dibuat garis sejajar sisi-sisi segitiga seperti tampak pada gambar di bawah ini.Jika luas jajar genjang berturut-turut adalah 6 $cm^2$, 10 $cm^2$ dan 15 $cm^2$,maka luas segitiga $ABC$ adalah ….
- Diketahui bilangan empat digit $abcd$ yang semua angkanya berbeda. Jika $a$ × $d$ = $b$ × $c$ maka bilangan empat digit $abcd$ terbesar adalah ….
- Suatu kelas yang terdiri dari 30 siswa membentuk dua kelompok belajar A dan B yang masing-masing beranggotakan 20 dan 10 siswa. Nilai rata-rata hasil ulangan kelompok A dan B masing-masing 70 dan 60. Selanjutnya 5 siswa dari kelompok belajar A pindah ke kelompok B sehingga didapatkan rata-rata hasil ulangan dari kedua kelompok sama. Jika nilai ulangan dari 5 siswa yang pindah kelompok tersebut berurutan, maka nilai ulangan terkecil dari 5 siswa tersebut adalah ….
- Terdapat 5 petak yang bisa diisi dengan huruf a atau b.
 Sebagai contoh,
Sebagai contoh,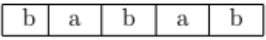 Ada berapa banyak susunan huruf a atau b dalam lima petak yang berawal atau berakhir dengan huruf b?
Ada berapa banyak susunan huruf a atau b dalam lima petak yang berawal atau berakhir dengan huruf b? - Peserta lomba “Pemburu Harta Karun” harus melewati tepat satu kali semua lintasan sesuai dengan arah panah seperti pada gambar di bawah. Peserta yang melewati setiap pos (K, L, M, N dan J) harus mengambil satu bendera yang tersedia di pos tersebut (di setiap pos disediakan beberapa bendera). Pemenang lomba adalah peserta yang berhasil mengumpulkan bendera terbanyak. Berapa banyak bendera maksimal yang harus dikumpulkan supaya menjadi juara?

SOAL URAIAN
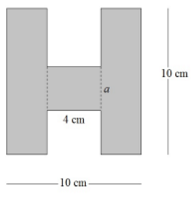
- Luas daerah yang diarsir di bawah ini adalah 80 $cm^2$. Tentukan nilai $a$.
- Ucok dan Alisa bersepeda mengelilingi lapangan secara bersamaan dengan arah yang sama dan berangkat dari titik yang sama. Ucok dan Alisa masing-masing bersepeda dengan kecepatan 8 km/jam dan 4 km/jam. Setelah menempuh satu putaran Ucok beristirahat 5 menit, kemudian dia
bersepeda kembali. Setelah 20 menit bersepeda Ucok dan Alisa berada di posisi yang sama. Berapakah keliling lapangan tersebut? - Andi menuliskan semua bilangan empat digit yang memenuhi tiga sifat berikut:
• Kelipatan 9
• Angka ribuan adalah 3
• Angka satuan ditambah angka ribuan sama dengan angka puluhan ditambah angka ratusan.
Tentukan semua bilangan yang ditulis Andi. - Toko Roti “Puri Indah” menjual roti isi coklat seharga Rp2.000,00 per potong, roti isi kelapa seharga Rp1.500,00 per potong dan roti isi keju seharga Rp2.500,00 per potong. Ibu Ayu membeli semua jenis roti tersebut sebanyak 10 potong dengan harga Rp20.000,00. Tentukan semua kemungkinan roti yang dibeli oleh Ibu Ayu.
- Perbandingan banyak siswa kelas $A, B$ dan $C$ adalah 2:3:4. Perbandingan nilai rata-rata ujian matematika kelas $A, B$ dan $C$ adalah 4:3:2. Rentang nilai ujian matematika 0 sampai dengan 100. Tentukan nilai rata-rata terbesar seluruh siswa yang mungkin.
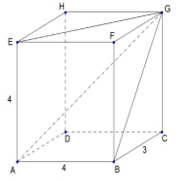
- Bila panjang rusuk-rusuk balok $ABCD.EFGH$ adalah 4 cm × 3 cm × 4 cm seperti tampak pada gambar di bawah. Tentukan perbandingan luas permukaan limas $G.ABFE$ dengan permukaan balok $ABCD.EFGH$.
- Mahatma memiliki 10 butir kelereng. Kemudian Mahatma bergabung dalam sekelompok anak untuk bermain kelereng. Pemenang akan men-
dapatkan 1 kelereng dari tiap-tiap anak yang bermain. Jika setelah bermain lima kali, kelereng Mahatma menjadi 31 butir, maka berapakah banyak anak yang bermain bersama Mahatma? - Sebuah mesin memiliki tiga roda A, B, dan C yang dihubungkan dengan tali karet seperti tampak pada gambar. Sebelum mesin dihidupkan ketiga
roda harus dalam posisi standar yaitu huruf-huruf roda harus terbaca tegak. Jika roda A, B, dan C masing memiliki jari-jari 14 cm, 21 cm, dan 28 cm. Setelah mesin dihidupkan, pada putaran ke berapa masing-masing huruf pada roda tersebut kembali dalam keadaan standar untuk pertama kalinya (gunakan $\pi =\frac{22}{7}$)?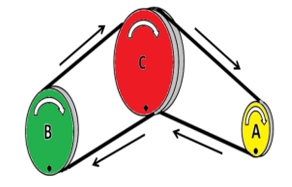
- Diketahui sebuah tabung dengan jari-jari 2 cm dan tinggi 20 cm, dan sebuah kerucut padat dengan jari-jari dan tinggi sama dengan tabung tersebut. Kerucut dipotong setengah dari tinggi tabung sejajar alas. Jika bagian bawah kerucut terpotong tersebut dimasukan ke dalam tabung maka volume ruang di dalam tabung dan di luar kerucut terpotong (seperti tampak pada gambar) adalah ….
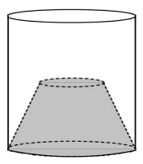
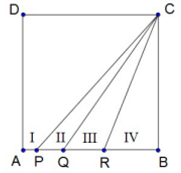
- Gambar di bawah ini merupakan persegi ABCD. Jika AP : PQ : QR : RB = 1 : 2 : 3 : 4 maka tentukan perbandingan luas daerah I : II : III : IV.
- Tabel berikut ini menunjukkan banyak siswa SD yang mengunjungi perpustakaan dalam enam hari.

Rata-rata pengunjung perpustakaan itu dalam enam hari ternyata sama banyaknya dengan salah satu hari kunjungan itu. Apabila 17A dan 1B3 menyatakan bilangan tiga digit, tentukan nilai A dan B yang memenuhi. - Selama pelatihan OSN siswa-siswa diinapkan di suatu wisma. Tersedia beberapa kamar kosong. Bila setiap kamar akan diisi tiga siswa, maka akan ada delapan siswa yang tidak mendapat kamar. Tapi bila setiap kamar akan diisi empat siswa, maka akan tersisa empat kamar yang tidak terisi. Berapa banyak siswa yang akan mengikuti pelatihan OSN tersebut?
- How many difference rectangles are there in the following figure?