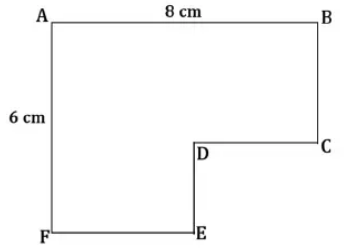
- Pada gambar dibawah ini, diketahui $AF$ sejajar $BC$ dan $DE$, sedangkan $AB$ sejajar $FE$ dan $DC$. Jika $AB=8$ cm, $AF=6$ m, maka berapakah keliling dari $ABCDEF$?
- Diberikan enam bilangan $A,B,C,D,E,F$ yang memenuhi: $$A+2=B-4^2=C+7=D+4=E+3^2=F-3^2$$ Di antara $A,B,C,D,E,F$, manakah yang bernilai paling besar?
- Andika beserta istri dan tiga orang anaknya akan berfoto. Berapa banyak cara posisi foto mereka jika Andika dan istri harus berdampingan?
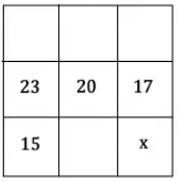
- Gambar dibawah ini merupakan “Magic Square” yaitu jumlah bilangan pada setiap baris, kolom dan diagonal adalah sama. Tentukan nilai dari $x$.
- Diketahui tiga bilangan prima $A,B$, dan $C$ memenuhi $499A+103B+102C=2025$. Berapakah nilai dari $A+B-C$?
- Jika diketahui kriptaritem berikut: $$\text{ROTI + ROTI = KEJU.}$$ Setiap huruf mewakili satu digit berbeda tanpa 0. Berapakah nilai terkecil yang mungkin dari KEJU?
- Dari digit 0, 1, 2, 3, 6, 7, 9 disusun bilangan genap 4 digit yang digit-digitnya berbeda. Ada berapa banyak bilangan yang dapat dibentuk?
- Dua buah dadu, masing-masing berwarna merah dan hijau, dilempar bersamaan. Misalkan pada dadu merah muncul mata dadu $a$ dan pada dadu hijau muncul mata dadu $b$. Selanjutnya dihitung $a\times b$ dan $a+b$. Ada berapa banyak pasangan $(a,b)$ mungkin sehingga selisih dari $a\times b$ dan $a+b$ merupakan bilangan kuadrat?
(Contoh. $a=2, b=1$, maka $(a+b)-(a\times b)=(2+1)-(2\times 1)=1=1^2)$. - Terdapat tiga tabung $A, B$ dan $C$. Diketahui jari-jari tabung $A,B$ dan $C$ berturut-turut adalah 8 cm, 3 cm dan 2 cm. Sedangkan tinggi tabung $A,B$ dan $C$ berturut-turut adalah 15 cm, 7 cm dan 3 cm. Pada mulanya tabung $A$ kosong, akan diisi air dengan menggunakan tabung $B$ atau $C$. Jika setiap kali pengisian, tidak boleh ada air yang tersisa pada tabung $B$ atau $C$ dan boleh ada air yang tumpah dari tabung $A$, maka minimal berapa banyak proses pengisian agar tabung $A$ penuh?
- Sebuah pesawat berangkat dari Kota A pada pukul 08.20 hari Sabtu dan tiba di Kota B pada pukul 06.35 hari Minggu. Diketahui durasi penerbangan adalah 14 jam 15 menit. Berapakah perbedaan waktu antara Kota A dan Kota B? (Tulis: “Kota B_ jam lebih (maju/mundur) dari Kota A.”)
- Pada sebuah persegi $ABCD$. Titik $K$ adalah titik tengah sisi $BC$, titik $H$ adalah titik tengah sisi $AB$, dan titik $O$ adalah titik pusat persegi. Dibentuk bangun segi empat $DKOH$. Jika luas bangun $DKOH$ adalah 9 satuan luas, tentukan panjang sisi $AB$.
- Andi, Bardi, Clara, Dora dan Endang tinggal di satu RW yang terdiri dari RT 1 dan RT 2. Diketahui tepat 2 orang tinggal di RT 1 dan 3 orang tinggal di RT 2.
– Bardi tinggal di RT yang berbeda dengan Endang dan Clara
– Dora tinggal di RT yang berbeda dengan Andi dan Clara
Siapa yang tinggal di RT 1? - Diberikan persegi panjang $ABCD$, dengan $\angle BCA=30^o$. Titik $P$ pada $AD$ dan $Q$ pada $BC$ sehingga $PQ$ sejajar $AB$ dan memotong diagonal $AC$ di titik $R$. Jika $x=\angle ARQ$ dan $y=\angle ARP$. Tentukan nilai $3y-x$.
- Bilangan 4 angka berbeda $\overline{ABCD}$, dengan $\overline{AB}$ habis dibagi 5, $\overline{ABC}$ habis dibagi 4, dan $\overline{ABCD}$ habis dibagi 3, maka nilai terbesar dari $\overline{ABCD}$ adalah …
- Diberikan persegi $ABCD$. Sebuah garis memotong $AD, AC$ dan $BC$ berturut-turut di titik $E,F$ dan $G$ seperti pada gambar berikut.
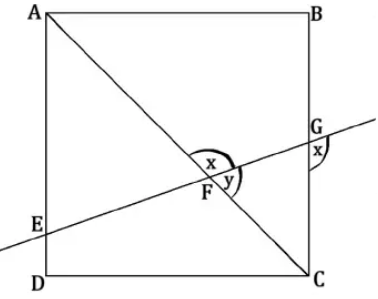
Nilai dari $3y-x=…$ - Sebuah klub basket memiliki 15 siswa dan 20 siswi. Setiap bulan jumlah siswa bertambah 2 orang dan jumlah siswi bertambah 1 orang. Berapa jumlah total anggota klub saat banyaknya siswa dan siswi sama?
- Jika diketahui $$A=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{2025}\text{ dan }B=\frac{3}{2}+\frac{4}{3}+\frac{5}{4}+…+\frac{2026}{2025}$$ maka nilai dari $(2026+B)-(2025+A)=…$
Keranjang Belanja
