- Suatu bilangan bulat positif empat digit memiliki keempat sifat berikut.
a) Kurang dari 2025
b) Jumlah keempat digitnya sama dengan 24
c) Jumlah digit ribuan dan ratusan sama dengan jumlah dua digit lainnya dikurangi 4
d) Memiliki tepat tiga faktor prima berbeda yang jumlahnya kurang dari 100.
Bilangan tersebut adalah … - Besar sembilan sudut dalam tiga segitiga adalah $n_1\text{ }^o, n_2\text{ }^o, …, n_9\text{ }^o$, dengan $n_1, n_2, …, n_9$ bilangan bulat positif yang membentuk barisan aritmatika dengan beda positif, Jika besar salah satu sudut adalah $78^o$, maka jumlah semua nilai $n_1$ yang mungkin adalah …
- Disuatu SMP terdapat klub OSN yang seluruh anggotanya adalah siswa kelas 7 dan 8. Dari semua anggota klub OSN yang merupakan siswa kelas 7, terdapat 60% siswa yang kidal. Sementara, dari semua anggota klub OSN yang merupakan siswa kelas 8, hanya 10% yang kidal. Jika banyaknya anggota klub OSN yang kidal sama dengan yang tidak kidal, maka persentase anggota klub OSN yang merupakan siswa kelas 7 adalah …
- Dalam rangka menyambut hari kemerdekaan, sebuah taman berbentuk segitiga sama sisi dengan panjang setiap sisinya $4\sqrt{3}$ meter akan dihiasi dengan 4 lampu dan tali hias. Satu lampu utama akan di pasang tepat di pusat taman sehingga jarak lampu ke ketiga titik sudut taman sama. Sementara, tiga lampu lainnya akan dipasang di tengah setiap sisi taman dengan ketinggian sama dengan lampu utama. Setiap lampu akan dihubungkan dengan lampu lainnya menggunakan tali hias. Jika setiap lampu akan dihubungkan dengan lampu lainnya menggunakan tali hias dan tali hias hanya di jual dalam kelipatan 1 meter, maka panjang minimum tali hias yang harus dibeli adalah … meter.
- Bilangan real $a,b,c$ memenuhi persamaan $$a+b+c=0\text{ }\text{dan}\text{ }a^2+b^2+c^2=12$$ Nilai maksimum dari $(a^3+b^3+c^3)^2$ adalah …
- Tiga orang yaitu, Ali, Budi dan Cika sedang bermain game dirumah. Di akhir permainan, layar menampilkan total skor 6208 poin yang merupakan jumlah dari tiga skor berbeda milik Ali, Budi, dan Cika. Masing-masing skor milik Ali, Budi dan Cika dapat dinyatakan dalam bentuk perpangkatan 2 dengan pangkat bilangan bulat positif. Jika setiap skor mereka dinyatakan dalam bentuk tersebut, maka jumlah pangkat dari ketiga skor mereka adalah …
- Suatu bilangan bulat $N=(a_na_{n-1}…a_2a_1a_0)_b$ dalam basis suatu bilangan bulat positif $b>1$ didefinisikan sebagai berikut $$N=a_nb^n+a_{n-1}b^{n-1}+…+a_2b^2+a_1b+a_0$$ Dengan $a_k$ bilangan bulat dan $0\le a_k < b$, untuk $k=0,1,2,…,n$.
Jika $(1P3)_m=(2Q4)_{m-2}$ dan $m<8$, maka nilai dari $m+P+Q$ adalah … - Dalam sebuah pentas menyanyi, Adi, Bobi, Cica dan Debi menerima honor dalam bentuk uang seratus ribuan dengan total Rp12.500.000. Honor akan dibagi dengan kesepakatan sebagai berikut.
a) Uang tatap dalam bentuk seratus ribuan
b) Adi menerima honor sebanyak setengah dari jumlah honor ketiga teman lainnya
c) Bobi menerima honor sebanyak sepertiga dari jumlah honor ketiga teman lainnya
d) Cica menerima honor sebanyak seperempat dari jumlah honor ketiga teman lainnya
e) Sisa honor yang sudah tidak dapat dibagi lagi menggunakan kesepakatan nomor 1 sampai 4, akan diberikan semuanya kepada orang yang mendapatkan honor yang paling sedikit.
Jumlah honor yang diterima Adi dan Cica adalah … lembar seratus ribuan. - Pak Wayan melakukan perjalanan pergi pulang dari Kota A ke Kota C melalui Kota B. Tersedia 8 jalur berbeda dari Kota A ke Kota B (disebut jalur 1 sampai 8) dan 6 jalur berbeda dari Kota B ke Kota C (disebut jalur 9 sampai 14). Saat pergi, ia menggunakan mobil berpelat genap, sementara saat pulang, tersedia 10 mobil yang dapat dipilih dengan 6 pelat nomor ganjil dan 4 pelat nomor genap.
Terdapat aturan khusus untuk jalur perjalanan sebagai berikut.
a) Untuk perjalanan dari Kota A ke Kota B atau sebaliknya, mobil yang berpelat nomor ganjil hanya boleh melewati jalur dengan nomor bukan bilangan prima
b) Setiap jalur hanya boleh dilewati satu kali
Banyaknya cara Pak Wayan pergi-pulang dari Kota A ke Kota C adalah … - Terdapat dua kotak misterius, yaitu kotak A dan kotak B. Di dalam setiap kotak terdapat suatu bilangan rahasia. Sementara, di luar kedua kotak terdapat sebuah petunjuk berikut.
“Jika bilangan dalam kotak A dikurangi dua kali akar dari hasil penjumlahan bilangan dalam kotak A dengan tiga, hasilnya sama dengan hasil penjumlahan dari negatif bilangan dalam kotak B dengan dua kali akar dari hasil penjumlahan bilangan dalam kotak B dengan satu”.
Dengan petunjuk tersebut, bilangan bulat terbesar yang mungkin diperoleh dari hasil penjumlahan bilangan dalam kotak A dan kotak B adalah … - Misalkan FPB dari bilangan bulat positif $a$ dan $b$ adalah $p$, serta KPK dari $a$ dan $b$ adalah $q$.
Jika $p+q=2025$ dan $c=\frac{a+b}{p}$, maka nilai $c$ terkecil yang mungkin adalah … - Dari semua bilangan bulat positif yang kurang dari atau sama dengan 2025, akan dipilih $n$ bilangan berbeda sehingga tidak ada yang selisihnya 2 ataupun 5. Nilai $n$ terbesar yang mungkin adalah …
- Diketahui jajargenjang $ABCD$, dengan $BC=2AB$. Dua titik berbeda $E$ dan $F$ terletak pada perpanjangan sisi $AB$ dengan $AB=AE=BF$. Jika titik $P$ merupakan titik potong garis $CE$ dan $DF$, maka besar sudut $EPF$ adalah …
- Ani dan Budi bermain balok-balok kecil dengan panjang $a$ cm, lebar $b$ cm dan tinggi $c$ cm. Dengan menggunakan balok-balok kecil tersebut, Ani menyusun balok $ABCD.EFGH$ dengan komposisi ukuran $9\times 5\times 3$ balok-balok kecil, seperti terlihat pada Gambar (a). Sementara, Budi juga menggunakan balok-balok kecil yang sama untuk menyusun balok $PQRSTUVW$ dengan komposisi ukuran $12\times 2\times 8$ balok-balok kecil, seperti terlihat pada Gambar (b).
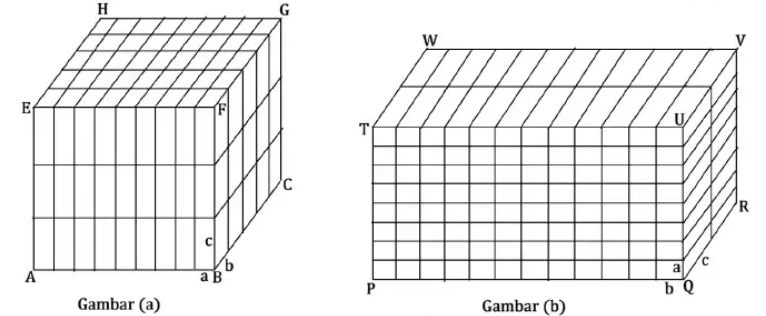
Diketahui volume balok $ABCD.EFGH$ sama dengan 2025 $\text{cm}^3$, panjang $AB$ sama dengan panjang $PQ$, panjang $BC$ 2,5 cm lebih pendek dari panjang $QR$, dan panjang $QU$ 1 cm lebih panjang dari panjang $BF$. Luas permukaan balok $PQRSTUVW$ adalah … $\text{cm}^2$. - Suatu permainan melibatkan kegiatan memasukkan bola yang akan menggelinding memasuki suatu jejaring pipa sehingga akhirnya bola akan masuk ke salah satu dari kotak $A,B$ atau $C$ seperti terlihat pada gambar.
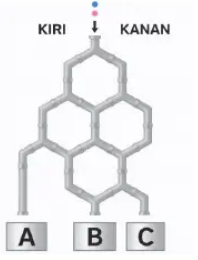
Tito melakukan permainan tersebut dengan memasukkan dua buah bola secara berurutan satu persatu. Diketahui bahwa pada setiap persimpangan, peluang bola memasuki pipa kiri adalah dua kali peluang bola memasuki pipa kanan. Jika peluang kedua bola masuk pada dua kotak berbeda dapat dinyatakan dalam pecahan paling sederhana $\frac{m}{n}$, maka nilai $n-m=$ … - Pada suatu bangun setengah lingkaran berdiameter $AB=16\sqrt{3}$ cm, titik $C$ dan $D$ terletak pada setengah lingkaran tersebut sehingga panjang busur $AC$ = panjang busur $CD$ = panjang busur $DB$. Melalui titik $C$ dibuat garis $m$ yang tegak lurus dengan garis $BD$, sehingga garis $m$ dan $BD$ berpotongan di titik $E$. Selanjutnya, $AE$ memotong setangah lingkaran tersebut di $F$. Misalkan garis $BF$ berpotongan dengan garis $CE$ di $G$, jarak titik $G$ ke diameter $AB$ sama dengan … cm.
- Aurel, Bella, Candra dan Dimas memainkan permainan catur dengan ketentuan yaitu pemain yang menang memperoleh 2 poin. Pemain yang bermain seri memperoleh 1 poin, dan pemain yang kalah memperoleh 0 poin. Setiap pemain akan bermain satu kali melawan maisng-masing pemain lainnya. Pemain dengan total poin tertinggi di akhir permainan akan menjadi juara. Jika terdapat lebih dari satu pemain memiliki poin tertinggi yang sama, maka juara ditentukan melalui undian di antara pemain yang memiliki poin tertinggi. Masing-masing pemain yang mengikuti undian berpeluang sama untuk menjadi juara. Hasil permainan yang telah diketahui adalah Aurel kalah dari Bella, Aurel menang dari Candra, Bella kalah dari Dimas, dan Candra kalah dari Dimas. Permainan yang belum dimainkan adalah Aurel melawan Dimas dan Bella melawan Candra. Diasumsikan peluang setiap orang untuk menang, seri dan kalah di setiap permainan yang tersisa adalah sama. Jika peluang terbesar seorang pemain untuk menjadi juara dapat dinyatakan dalam bentuk pecahan paling sederhana $\frac{p}{q}$, maka nilai dari $p+q$ adalah …
- Perhatikan gambar segienam beraturan ABCDEF berikut.
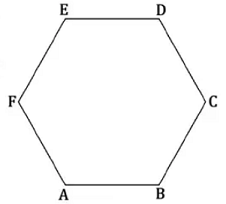
Diketahui panjang sisi $BC$ adalah $2\sqrt{21}$ cm dan titik $G$ ditengah-tengah sisi $BC$. Irisan segitiga $AGE$ dan segitiga $DFG$ adalah segiempat yang memiliki luas $p\sqrt{q}$ $\text{cm}^2$. Jika FPB $(p,q)=1$, maka $p+q$ = … - Terdapat himpunan yang memiliki lima sifat sebagai berikut.
a) Memiliki setidaknya 2 anggota
b) Semua anggotanya bilangan bulat positif yang berbeda
c) Hasil perkalian semua anggotanya adalah kelipatan dari hasil perkalian semua bilangan bulat positif yang tidak lebih dari banyaknya anggotanya
d) Selisih dari anggota terbesar dan terkecilnya kurang dari banyaknya anggota
e) Hasil penjumlahan semua anggotanya adalah 2025.
Banyaknya himpunan yang memiliki kelima sifat tersebut adalah … - Jika $x,y,z$ adalah bilangan positif yang memenuhi system persamaan $$x(x+y)+z(x-y)=65$$ $$y(y+z)+x(y-z)=296$$ $$z(z+x)+y(z-x)=104$$ Nilai dari $x+y-z$ adalah …
Keranjang Belanja
