Aplikasi Tiga Prinsip, Permutasi dan Kombinasi

• Contoh 1. Berapa banyak bilangan bulat antara $0$ dan $10^5$ yang jumlah digitnya sama dengan $8$?
  Solusi: Pertanyaannya setara dengan pertanyaan berikut:
  Berapa banyak permutasi $(x_1, x_2, x_3, x_4, x_5)$ dari lima bilangan bulat non-negatif yang ada sehingga $$x_1+x_2+x_3+x_4+x_5=8?$$ Oleh karena itu jawaban nya adalah $\binom{12}{4}=495.$
• Contoh 2. Misalkan $A_1A_2…A_{200}$ menjadi poligon cembung beraturan bersisi $200$. Buatlah diagonal-diagonalnya $A_iA_{i+9},i=1, 2,…, 200$, dengan $A_{i+200} = A_i$ untuk $1\le i\le 9$. Berapa banyak titik potong berbeda yang terbentuk di dalam poligon oleh $200$ diagonal ini?
  Solusi: Untuk setiap diagonal $A_iA_{i+9}$, kedua diagonalnya $A_{i+j}A_{i+j+9}$ dan $A_{i+j-9}A_{i+j}$ untuk $j=1,2,…,8$, memotong $A_iA_{i+9}$, di mana kita memiliki sebuah konvensi $A_m=A_{m+200}$ untuk $-9\le m\le -1$. Dengan demikian, jumlah titik potong pada diagonalnya adalah $A_iA_{i+9}$ adalah $2\times 8=16.$
  Karena panjang ke-$200$ diagonal ini sama, semuanya bersinggungan dengan lingkaran yang sama. Karena dari titik mana pun di luar lingkaran, tepat dua garis singgung ke lingkaran dapat ditarik, maka tiga dari $200$ diagonal tersebut tidak dapat berpotongan di satu titik yang sama. Dengan demikian, jumlah total titik potong interior dari $200$ diagonal tersebut adalah $\frac{200\cdot 16}{2}=1600$.
• Contoh 3. Temukan jumlah 6-tuple terurut $(x_1,x_2,x_3,x_4,x_5,x_6)$ bilangan bulat positif yang memenuhi $$x_1+x_2+x_3+3x_4+3x_5+5x_6=21.$$
  Solusi: Misalkan $x_1+x_2+x_3=x,x_4+x_5=y,x_6=z$, maka $x\ge 3,y\ge 2,z\ge 1.$ Mempertimbangkan persamaan Diophantine $x+3y+5z=21$ dengan $x\ge 3,y\ge 2,z\ge 1$. Maka $$5z=21-x-3y\le 12\Rightarrow z\le 2.$$ Ketika $z=1$, maka $x+3y=16\Rightarrow x=1+3t,y=5-t$, maka $(x,y)=$ (10, 2), (7, 3), (4, 4).
  Ketika $z=2$, maka $x+3y=11\Rightarrow x=2+3t,y=3-t$, maka $(x,y)=$ (5, 2) saja.
  Jadi, $(x,y,z)$ = (10, 2, 1), (7, 3, 1), (4, 4, 1), (5, 2, 2).
  Untuk persamaan $x_1+x_2+x_3=x$, jumlah solusinya adalah $\binom{x-1}{2};$ persamaan $x_4+x_5=y$ memiliki $y-1$ solusi berbeda, maka jumlah solusi untuk $(x_1,x_2,x_3,x_4,x_5,x_6)$ diberikan oleh $$\binom{9}{2}\cdot(2-1)+\binom{6}{2}(3-1)+\binom{3}{2}(4-1)+\binom{4}{2}(2-1)=36+30+9+6=81.$$
• Contoh 4. Tentukan banyaknya himpunan bagian beranggotakan $4$ elemen $\{a,b,c,d\}$ dari $\{1,2,3,4,…,20\}$ sehingga $a+b+c+d$ habis dibagi $3$.
  Solusi: Bagilah himpunan $S=\{1,2,…,20\}$ menjadi tiga subhimpunan menurut sisa mod 3: $C_0,C_1,C_2$ dan $|C_0|=6,|C_1|+|C_2|=7.$
  (i)     Ketika $a,b,c,d$ semuanya datang dari $C_0$, jumlah subset $4$ elemen adalah $\binom{6}{4}=15;$
  (ii)    Ketika $2$ dari $\{a,b,c,d\}$ berasal dari $C_0$, yang ketiga dari $C_1$ dan yang keempat dari $C_2$, maka banyaknya himpunan bagian yang terdiri dari $4$ elemen adalah $\binom{6}{2}\cdot\binom{7}{1}^2=735.$
  (iii)   Ketika tiga dari $a,b,c,d$ berasal dari $C_1$ atau dari $C_2$, dan keempat elemen adalah dari $C_0$, maka banyaknya himpunan bagian yang terdiri dari $4$ elemen adalah $$\binom{7}{3}\cdot\binom{6}{1}+\binom{7}{3}\cdot\binom{6}{1}=420;$$ 
  (iv)   Ketika $2$ dari $\{a,b,c,d\}$ berasal dari $C_1$ dan $2$ lainnya berasal dari $C_2$, maka banyaknya himpunan bagian dari $4$ elemen adalah $\binom{7}{2}^2=21^2=441;$
  Jadi, jumlah bilangan dari $4$ elemen adalah $15+735+420+441=1611$.

Aplikasi Korespondensi dan Bijeksi

Teorema I. Misalkan $M$ dan $N$ menjadi dua himpunan berhingga. Jika terdapat injeksi dari $M$ ke $N$, maka $|M|\le |N|$; jika terdapat surjeksi dari $M$ ke $N$, maka $|M|\ge |N|$; jika terdapat bijeksi dari $M$ ke $N$, maka $|M|=|N|$.

• Contoh 5. Untuk setiap himpunan berhingga tak kosong $A$ bilangan riil, misalkan $s(A)$ adalah jumlah elemen-elemen di $A$. Terdapat tepat $61$ subset $A$ berelemen $3$ dari $\{1,…,23\}$ dengan $s(A)=36$. Tentukan banyaknya subset berelemen $3$ dari $\{1,…,23\}$ dengan $s(A)<36$.
  Solusi: Untuk setiap subset $3$ elemen $x=\{a,b,c\}$ dari himpunan $M=\{1,2,3,…,23\}$ dengan $a+b+c<36$, definisikan pemetaan $f(x)=\{24-a,24-b,24-c\}$. Maka, $f$ adalah bijeksi antara himpunan $C_1$ dari ketiga subset elemen $M$ dengan $a+b+c>36$. Oleh karena itu, $|C_1|=|C_2|$.
  Karena terdapat total $\binom{23}{3}=1771$ subset $3$ elemen berbeda dari $M$, maka $$|C_1|=\frac{1}{2}(1771-61)=855.$$ 
• Contoh 6. Bagilah setiap sisi segitiga sama sisi $XYZ$ dengan sisi $n$ menjadi $n$ bagian yang sama besar. Dengan memasukkan garis-garis sejajar sisi $XYZ$ yang melalui titik-titik pembagian ini, kita memperoleh kisi-kisi yang dibentuk oleh $n^2$ segitiga sama sisi yang sama besar dengan sisi $1$, seperti yang ditunjukkan pada diagram berikut. Tentukan jumlah jajargenjang yang terdapat dalam kisi-kisi tersebut.
  
  
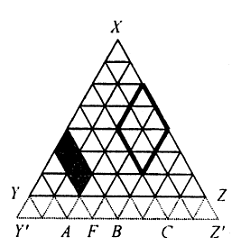
  Solusi: Gunakan $S_{yz}$ untuk menunjukkan himpunan semua jajaran genjang dalam grid yang memiliki sisi yang sejajar dengan garis $XY$ atau $XZ$. Demikian pula, kita definisikan himpunan $S_{zx}$ dan $S_{xy}$. Dengan simetris kita memiliki $|S_{yz}|=|S_{xy}|=|S_{zx}|$, jadi jawabannya adalah $3|S_{yz}|$.
  Untuk mendapatkan $|S_{yz}|$, kita perluas sinar $XY$ satu satuan ke $Y’$ dan sinar $XZ$ satu satuan ke $Z’$. Misalkan $p$ adalah jajargenjang di $S_{yz}$. Kemudian, dengan memperluas sisi-sisi $p$ sehingga kita memiliki empat titik potong pada $Y’Z’$. Sebaliknya, setiap empat titik pada $Y’Z’$ menentukan jajargenjang unik $p$ di $S_{yz}$.
  Misalnya, pada gambar, jajargenjang berarsir yang bersesuaian dengan $\{Y’,A,F,B\}$ dan jajargenjang bersisi tebal yang bersesuaian dengan $\{A,B,C,Z’\}$. Dengan demikian, kita mendapatkan bijeksi antara $S_{yz}$ dan himpunan grup empat titik pada $Y’Z’$. Oleh karena itu, jawabannya adalah $3\binom{n+2}{4}.$
• Contoh 7. Terdapat $n(n\ge 6)$ titik pada sebuah lingkaran, dan setiap dua titik dihubungkan oleh sebuah ruas garis. Misalkan ada tiga ruas garis yang tidak berpotongan, maka setiap tiga ruas garis yang berpotongan membentuk segitiga di dalam lingkaran. Tentukan jumlah segitiga yang terbentuk.
  Solusi: Kita menyebut titik pada lingkaran sebagai titik luar dan titik dalam lingkaran sebagai titik dalam. Segitiga dapat diklasifikasikan menjadi empat kelas:
  $C_1:$ ketiga titik sudutnya adalah titik eksterior. Misalkan $|C_1|$ adalah $I_1;$
  $C_2:$ dua titik sudut merupakan titik luar, dan satu titik sudut merupakan titik dalam. Misalkan $|C_2|$ adalah $I_2;$
  $C_3:$ satu titik sudutnya eksterior dan dua yang lain interior. Misalkan $|C_3|$ adalah $I_3;$
  $C_4:$ ketiga titik sudutnya merupakan titik dalam. Misalkan $|C_4$ adalah $I_4;$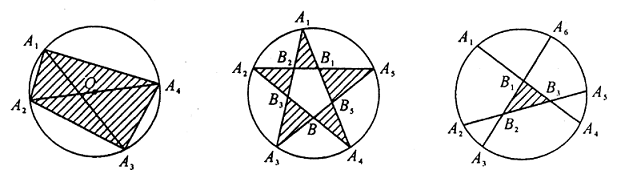
  
  
  Sudah jelas bahwa $I_1= ^nC_3.$
  Selanjutnya, seperti yang ditunjukkan pada diagram (1) di atas, setiap empat titik pada lingkaran membentuk empat segitiga di $C_2$, dan sebaliknya. Dengan demikian, $I_2 = 4\cdot ^nC_4.$
  Demikian pula, seperti yang ditunjukkan pada diagram (2) di atas, setiap lima titik pada lingkaran membentuk lima segitiga di $C_3$, dan sebaliknya. Maka $I_3=5\cdot ^nC_5.$
  Terakhir, seperti yang ditunjukkan pada diagram (3) di atas, $I_4=^nC_6.$
  Jadi jumlah total segitiga adalah $^nC_3+4\cdot ^nC_4+5\cdot ^nC_5+ ^nC_6.$
• Contoh 8. Misalkan $M$ adalah himpunan dengan $|M|=n$. Jika $M$ memiliki $k$ subset berbeda $A_1,A_2,…,A_k$ sehingga $A_i\cap A_j\neq \emptyset$ untuk setiap $i,j \in\{1,2,…,k\}$. Tentukan nilai maksimum $k$.
  Solusi: (i) Untuk $M=\{a_1,a_2,…,a_n\}$ pertama-tama kami menunjukkan bahwa ada $2^{n-1}$ subset $M$ sehingga setiap dua dari mereka memiliki persimpangan yang tidak kosong. Hal ini karena $M$ memiliki total $2^{n-1}$ subset berbeda yang berisi $a_i$ untuk setiap $i$ tetap dalam $\{1,2,…,n\}$.
  (ii) Berikutnya kita tunjukkan bahwa untuk setiap $2^{n-1}+1$ subset berbeda dari $M$, pasti ada dua yang saling lepas. 
  Misalkan $B_1,B_2,…,B_{2^{n-1}}$ menjadi $2^{n-1}$ himpunan bagian berbeda dari $M$ sehingga masing-masing berisi elemen $a_n$, dan misalkan $B’_i$ menjadi himpunan yang saling melengkapi, yaitu $B’_i=M\smallsetminus B_i,i=1,2,…,2^{n-1}$. Karena $B_i$ yang berbeda mempunyai $B’_i$ yang berbeda, maka himpunan bagian $B_1,B_2,…,B_{2^{n-1}};B’_1,B’_2,…,B’_{2^{n-1}}$ terdiri dari semua $2^n$ himpunan bagian dari $M$.
  Kita dapat membentuk $2^{n-1}$ pasangan $(B_i,B’_i),i=1,2,…,2^{n-1}$ dengan menggunakan $2^n$ subset ini. Untuk setiap subset $2^{n-1}+1$ yang berbeda, berdasarkan prinsip pigeonhole, pasti ada dua subset yang berasal dari pasangan yang sama, sehingga keduanya harus saling lepas.