Lima Pusat Segitiga
Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Contoh Soal
Teorema I. Ketiga garis tengah suatu segitiga berpotongan di satu titik yang sama, dilambangkan dengan $G$, dan setiap garis tengah dibagi oleh $G$ menjadi dua bagian dengan rasio 2:1. Titik bersama $G$ disebut pusat gravitasi atau sentroid segitiga.
Konsekuensi Titik interior $P$ dari $\Delta ABC$ adalah pusat gravitasi $\Delta ABC$ jika dan hanya jika $$[PBC]=[PCA]=[PAB].$$ (Di sini notasi $[XYZ]$ menunjukkan luas $\Delta XYZ$.)
Teorema II. Pada setiap segitiga, garis bagi tiga sisi yang tegak lurus berpotongan di satu titik $O$. Titik $O$ merupakan pusat lingkaran luar segitiga, yang disebut pusat lingkaran luar segitiga.
Teorema III. Ketiga garis tinggi setiap segitiga $\Delta ABC$ berpotongan di satu titik persekutuan $H$, yang disebut orthocenter segitiga.
Teorema IV. Untuk setiap segitiga, garis bagi sudut dari tiga sudut dalamnya berpotongan di satu titik yang sama, dilambangkan dengan $I$ seperti biasa, yang disebut incenter (atau pusat dalam) segitiga. $I$ adalah pusat lingkaran dalam segitiga.
Teorema V. Untuk sebuah segitiga, garis bagi sudut dari satu sudut dalam dan dua sudut luar dari dua sudut dalam lainnya berpotongan di titik yang sama, yang disebut pusat segitiga. Ada tiga titik tersebut untuk sebuah segitiga, dan masing-masing merupakan pusat lingkaran yang dibatasi oleh segitiga tersebut.
Note: Pada segitiga sama kaki, pusat gravitasi, pusat lingkaran, pusat ortosentrum, dan pusat dalam semuanya berada pada sumbu simetris segitiga. Pada segitiga sama sisi, keempat pusat di atas berimpit pada satu titik, yang disebut pusat segitiga sama sisi.
Contoh Soal
- Untuk $\Delta ABC$ tertentu dengan $G$ sebagai pusat gravitasinya dan titik mana pun $M$ pada bidang yang sama, persamaan berikut selalu berlaku $$MA^2+MB^2+MC^2=GA^2+GB^2+GC^2+3MG^2.$$ Catatan: Kesimpulan memberikan definisi lain tentang pusat gravitasi segitiga $ABC$: Titik $G$ adalah pusat gravitasi $\Delta ABC$ jika dan hanya jika $$GA^2+GB^2+GC^2=\min\{MA^2+MB^2+MC^2\},$$ dimana $M$ bisa berupa titik mana pun pada bidang yang sama.
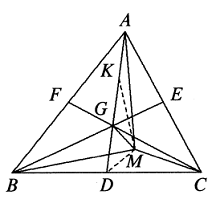
Solusi: Seperti yang ditunjukkan pada gambar, misalkan $G$ adalah pusat gravitasi dan ketiga mediannya masing-masing adalah $AD,BE,CF$. Gunakan $K$ untuk nyatakan titik tengah $AG$ dan hubungkan $MK,MD$. Maka $AK=KG=GD$ dan $$MB^2+MC^2=2(BD^2+MD^2),\text{ }\text{ }\text{ }\text{ }(15.1)$$ $$MA^2+MG^2=2(MK^2+GK^2),\text{ }\text{ }\text{ }\text{ }(15.2)$$ $$2(MD^2+MK^2)=4(MG^2+GK^2).\text{ }\text{ }\text{ }\text{ }(15.3)$$ Dengan $(15.1)+(15.2)+(15.3)$, $$MA^2+MB^2+MC^2=3MG^2+2(BD^2+GK^2)+4GK^2.$$ $$∵4GK^2=GA^2,$$ $$2(BD^2+GK^2)=2(BD^2+GD^2)=GB^2+GC^2,$$ $$∴MA^2+MB^2+MC^2=GA^2+GB^2+GC^2+3GM^2.$$ - Untuk setiap segitiga $ABC$, titik beratnya $G$, titik pusat lingkaran $O$, dan titik pusat ortosentrum $H$ adalah kolinear, dan $G$ berada di antara $O$ dan $H$ sehingga $HG=2OG$.
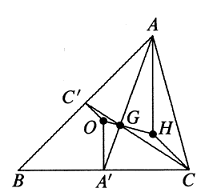
Solusi: Jika $A’$ dan $C’$ masing-masing merupakan titik tengah $BC$ dan $AB$, maka $G$ terletak pada $AA’$ dan $AG=2GA’$. Hubungkan $OA’$, $OG$. Misalkan $H’$ berada pada perpanjangan $OG$ sehingga $H’G=2GO$, maka $\Delta AGH’\sim\Delta A’OG$, yaitu $AH’||OA’$, maka $AH’\bot BC$ karena $OA’\bot BC$.
Demikian pula, $CH’\bot AB$.
Maka, $H’$ hanya orthocenter $H$. Kesimpulannya terbukti. - $H$ adalah orthocenter dari segitiga lancip $\Delta ABC$ dan $AH=p,BH=q,CH=r$. Tunjukkan bahwa $aqr+brp+cpq=abc$.
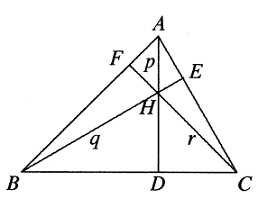
Solusi: Di bawah ini kita tunjukkan kesimpulannya dengan menggunakan metode trigonometri.
Misalkan $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$, dimana $R$ jari-jari keliling $\Delta ABC$. Maka $$\angle AHE=90^o-\angle DAC=\angle C$$ $$\Rightarrow p=\frac{AE}{\sin C}=\frac{AB\cos A}{\sin C}=2R\cos A.$$ Demikian pula, $q=2R\cos B$ dan $r=2R\cos C$. Oleh karena itu $$aqr+brp+cpq=abc$$ $$\Leftrightarrow 2R\sin A\cdot 2R\cos B\cdot 2R \cos C+2R\sin B\cdot 2R\cos C\cdot 2R\cos A+2R\sin C\cdot 2R\cos A\cdot 2R\cos B=2R\sin A\cdot 2R\sin B\cdot 2R\sin C$$ $$\Leftrightarrow \sin A\cos B\cos C+\sin B\cos C\cos A+\sin C\cos A \cos B=\sin A\sin B\sin C$$ $$\Leftrightarrow \tan A+\tan B\tan C=\tan A\tan B\tan C,$$ dan persamaan terakhir ini dikenal sebagai sifat dasar sebuah segitiga. - Pada segitiga lancip $ABC, D, E, F$ masing-masing adalah titik tengah sisi $BC, CA, AB$. Pada perpanjangan $EF, FD, DE$, ambil titik $P, Q, R$ masing-masing, sehingga $AP=BQ=CR$. Buktikan bahwa pusat lingkaran $\Delta PQR$ merupakan pusat lingkaran $\Delta ABC$.
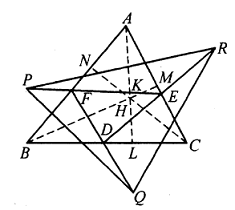
Solusi: Misalkan $AL,BM,CN$ adalah tinggi $\Delta ABC$, dan $H$ adalah orthocenter. Misalkan $EF$ memotong $AL$ di $K$. Maka
$AP^2$
$=PK^2+AK^2=PH^2-KH^2+AK^2$ $=PH^2(AK+KH)(AK-KH)$ $=PH^2+AH\cdot HL.$
Demikian pula, $$BQ^2=QH^2+BH\cdot HM\text{ dan}$$ $$CR^2=RH^2+CH\cdot HN.$$ Karena $AP=BQ=CR$ dan $ABLM,BCMN$ siklik, oleh karena itu $$AH\cdot HL=BH\cdot HM=CH\cdot HN,$$ sehingga $PH=QH=RH$, maka $H$ adalah pusat lingkaran $\Delta PQR$. - Pada $\Delta ABC$, titik-titik $D, E$ masing-masing terletak pada $AB, AC$ sehingga $DE||BC$. Lingkaran dalam $\Delta ADE$ menyinggung $DE$ di $M$, lingkaran luar sisi $BC$ pada $\Delta ABC$ menyinggung $BC$ di $N$. $BE$ dan $CD$ berpotongan di $P$. Buktikan bahwa $M, N, P$ kolinear.
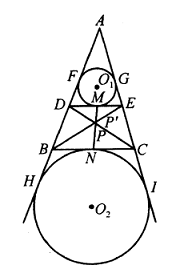
Solusi: Misalkan $BE$ dan $MN$ memotong $P’$. Karena $DE||BC$, $\frac{BP}{PE}=\frac{BC}{DE}$ dan $\frac{BP’}{P’E}=\frac{BN}{EM}$, cukup menunjukkan bahwa $$\frac{BN}{EM}=\frac{BC}{DE}\text{ atau }\frac{BN}{BC}=\frac{EM}{DE}.$$ Misalkan $O_1,O_2$ masing-masing adalah pusat lingkaran dalam dan lingkaran luar, dan $F, G, H, I$ adalah titik-titik singgung yang terkait, seperti yang ditunjukkan pada diagram di sebelah kanan. Maka $$EM=\frac{1}{2}(AE+DE-AD),$$ $$AH=AB+BH=AB+BN$$ $$=AI=\frac{1}{2}(AB+BC+AC),$$ sehingga $BN=AH-AB=\frac{1}{2}(AC+BC-AB)$. Karena $\Delta ADE\sim \Delta ABC$, maka memungkinkan untuk $$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}=k.$$ Maka $$\frac{BN}{BC}=\frac{\frac{1}{2}(AC+BC-AB)}{BC}=\frac{k(AE+DE-AD)}{2k\cdot DE} $$=\frac{AE+DE-AD}{2DE}=\frac{EM}{DE}.$$ Maka, kesimpulannya terbukti. - Lingkaran dalam $\Delta ABC$ berpusat di $I$ dan menyinggung sisi $AC, AB$ masing-masing di titik $E, F$. Misalkan $M$ adalah sebuah titik pada ruas garis $EF$. Buktikan bahwa luas $\Delta MAB$ dan $\Delta MAC$ sama jika dan hanya jika $MI\bot BC$.
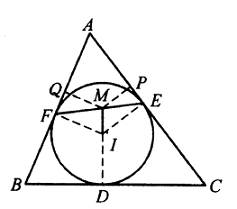
Solusi: Perkenalkan $MP\bot AC$ di $P$ dan $MQ\bot AB$ di $Q$. Misalkan $☉I$ menyentuh $BC$ di $D$, maka $ID\bot BC, IF\bot AB$ dan $IE\bot AC$.
$AF=AE$ menyiratkan bahwa $\angle AFM = \angle AEM$, maka $\Delta QFM\sim\Delta PEM$, sehingga $\frac{MQ}{MP}=\frac{MF}{ME}$. Maka $$\frac{[MAB]}{[MAC]}=\frac{MQ\cdot AB}{MP\cdot AC}=\frac{MF}{ME}\cdot \frac{AB}{AC},$$ maka $[MAB]=[MAC]$ jika dan hanya jika $$\frac{AB}{AC}=\frac{ME}{MF}.\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(15.4)$$ Di bawah ini membuktikan bahwa (15.4) berlaku jika dan hanya jika $MI\bot BC$.
Ketika $MI\bot BC$, maka $M$ ada di garis $ID$. $BDIF$ dan $CDIE$ keduanya siklik menyiratkan bahwa $$\angle MIF=\angle B,\text{ }\text{ }\text{ }\angle MIE=\angle C.$$ Kemudian penerapan aturan sinus pada $\Delta MIF$ dan $\Delta MIE$ memberikan $$\frac{MF}{\sin \angle MIF}=\frac{FI}{\sin \angle IMF}=\frac{IE}{\sin \angle EMI}=\frac{ME}{\sin \angle MIE},$$ yaitu $\frac{ME}{MF}=\frac{\sin \angle C}{\sin \angle B}=\frac{AB}{AC}$ karena aturan sinus lagi.
Sebaliknya, ketika $\frac{AB}{AC}=\frac{ME}{MF}$, misalkan garis $ID$ memotong $EF$ di $M’$, maka bukti di atas menunjukkan bahwa $\frac{M’E}{M’F}=\frac{AB}{AC}$, maka $\frac{ME}{MF}=\frac{M’E}{M’F}$ yang menyiratkan bahwa $M’=M$. Maka, $M$ ada di garis $ID$, yaitu $IM\bot BC$. - Misalkan $ABC$ adalah segitiga lancip dengan $\angle BAC=60^o$ dan $AB>AC$. Misalkan $I$ adalah incenter, dan $H$ adalah orthocenter segitiga $ABC$. Buktikan bahwa $2\angle AHI=3\angle ABC.$$
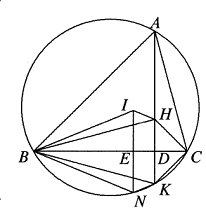
Solusi: Misalkan $D$ adalah titik potong garis $AH$ dan $BC$. Misalkan $K$ adalah titik potong lingkaran luar $O$ segitiga $ABC$ dan $AH$. Misalkan garis yang melalui $I$ tegak lurus $BC$ bertemu $BC$ dan busur minor $BC$ lingkaran luar $O$ di titik $E$ dan $N$, berturut-turut. Kita peroleh $$\angle BIC=180^o – (\angle IBC+\angle ICB)$$ $$=180^o-\frac{1}{2}(\angle ABC+\angle ACB)$$ $$=90^o+\frac{1}{2}\angle BAC=120^o,$$ $$\angle BNC=180^o-\angle BAC=120^o=\angle BIC.$$ Karena $IN\bot BC$, kita memiliki $IE=EN$ (jika tidak, katakanlah $IE<EN$, maka $\angle IBC<\angle NBC$ dan $\angle ICB<\angle NCB$ tetapi $\angle IBC+\angle ICB=\angle NBC+\angle NCB=60^o$, kontradiksi).
Sekarang, karena $H$ adalah orthocenter segitiga $ABC,HD=DK$. Dan karena $ED\bot IN$ dan $ED\bot HK$, kita simpulkan bahwa $IHKN$ adalah trapesium sama kaki dengan $IH=NK$. Maka $$\angle AHI=180^o-\angle IHK=180^o-\angle AKN=\angle ABN.$$ Karena $IE=EN$ dan $BE\bot IN$, segitiga $IBE$ dan $NBE$ kongruen. Oleh karena itu $$\angle NBE=\angle IBE=\angle IBC=\angle IBA=\frac{1}{2}\angle ABC$$ dan maka $$\angle AHI=\angle ABN=\frac{3}{2}\angle ABC.$$ - Diberikan segitiga lancip $ABC$, $O$ adalah pusat lingkaran luar dan $H$ adalah pusat lingkaran luar. Misalkan $A_1, B_1, C_1$ masing-masing adalah titik tengah sisi $BC, CA$, dan $AB$. Sinar-sinar $HA_1, HB_1, HC_1$ memotong lingkaran luar $\Delta ABC$ masing-masing di $A_0, B_0$, dan $C_0$. Buktikan bahwa $O, H$, dan $H_0$ kolinear jika $H_0$ adalah pusat lingkaran luar $\Delta A_0B_0C_0$.
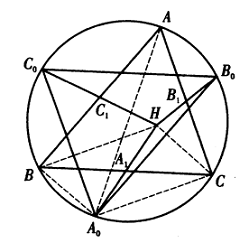
Solusi: Hubungkan $HB,HC,A_0B,A_0C,A_0A$. Orthocenter pada $\Delta ABC$ adalah $H$ menyiratkan bahwa $$\angle BHC=180^o-(90^o-\angle B)-(90^o-\angle C)$$ $$=\angle B+\angle C=180^o-\angle A=\angle BA_0C$$ Karena $HA_0$ melalui titik tengah $A_1$ pada $BC$, maka segiempat $BHCA_0$ adalah jajargenjang, maka $$\angle ACA_0=90^o.$$ Oleh karena itu $AA_0$ adalah diameter pada lingkaran luar $☉O$. Demikian, $CC_0,BB_0$ juga diameter pada $☉O$.
Jadi, Segitiga $ABC$ dan $A_0B_0C_0$ adalah simetris terhadap $O$, maka $H$ dan $H_0$ adalah simetris dalam $O$, yaitu $O$ titik tengah pada garis segmen $HH_0$. Kesimpulannya terbukti.
“Tell me and I forget. Teach me and I remember. Involve me and I learn.”
