Kekuatan Titik terhadap Lingkaran
Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Properti Utama Sumbu Radikal
- Contoh Soal
Temuan utama tentang daya suatu titik terhadap suatu lingkaran diperoleh dari teorema berikut:
Teorema I. Misalkan $☉O$ adalah sebuah lingkaran dengan jari-jari $R$. Untuk sebuah titik interior $P$ dari lingkaran, jika $AB$ adalah tali busur yang melalui $P$, maka nilai hasil kali $PA\cdot PB$ tidak bergantung pada pilihan tali busur yang melalui $P$. Secara khusus, nilai konstanta diberikan dengan mengambil $AB\bot OP$, sehingga $$R^2-OP^2.$$
Teorema II. Misalkan $⊙O$ adalah lingkaran dengan jari-jari $R$. Untuk titik $P$ yang berada di luar lingkaran atau pada keliling lingkaran, jika $PAB$ adalah garis transversal yang dimulai dari $P$, memotong lingkaran di $A$ dan $B$, maka nilai $PA\cdot PB$ tidak bergantung pada pilihan garis transversal yang melalui $P$. Secara khusus, nilai tersebut diberikan dengan mengambil garis singgung dari $P$ ke lingkaran sebagai garis transversal, sehingga menjadi $$OP^2-R^2.$$ Konsekuensi: Ketika ruas garis $AB$ dan $CD$ atau perpanjangannya berpotongan di titik $P$, maka $A, B, C, D$ adalah konsiklik jika dan hanya jika $AP\cdot PB=CP\cdot PD$. Jelas bahwa nilai $R^2-OP^2$ (ketika $P$ berada di dalam lingkaran) atau $OP^2-R^2$ (ketika $P$ berada di luar lingkaran) ditentukan oleh jarak $P$ dari lingkaran, sehingga didefinisikan sebagai pangkat titik $P$ terhadap lingkaran $☉O$.
Pangkat titik memiliki banyak aplikasi dalam menyelidiki pertanyaan tentang lingkaran, di mana konsep sumbu radikal didasarkan pada pangkat sebuah titik. Untuk setiap dua lingkaran non-konsentris $\omega_1$ dan $\omega_2$, tempat kedudukan semua titik dengan pangkat yang sama terhadap kedua lingkaran tersebut adalah sebuah garis, yang disebut sumbu radikal kedua lingkaran.
Teorema III. Ketika pusat-pusat tiga lingkaran $\omega_1,\omega_2,\omega_3$ tidak kolinear, terdapat tepat satu titik yang pangkatnya terhadap ketiga lingkaran tersebut sama. Titik ini disebut sebagai pusat radikal ketiga lingkaran.
Untuk tiga lingkaran yang diberikan, jika ada dua yang mempunyai sumbu radikal, maka ketiga sumbu radikal tersebut mungkin sejajar satu sama lain, atau bersamaan di pusat radikalnya.
Properti Utama Sumbu Radikal
- Dua lingkaran konsentris yang berbeda tidak memiliki sumbu radikal.
- Sumbu radikal ada untuk setiap dua lingkaran nonkonsentris yang terpisah dan sumbu radikal adalah garis yang tegak lurus terhadap garis yang menghubungkan pusat kedua lingkaran, yang melewati titik tengah dari empat garis singgung persekutuan dalam kedua lingkaran.
- Sumbu radikal ada untuk setiap dua lingkaran yang berpotongan, dan merupakan garis lurus yang melalui dua titik persekutuan pada lingkaran tersebut.
- Sumbu radikal ada untuk setiap dua lingkaran jika keduanya saling bersinggungan dan merupakan garis singgung persekutuan dalam pada titik persekutuan lingkaran tersebut.
Contoh Soal
- Segi lima $ABCDE$ terletak di dalam sebuah lingkaran, dengan diagonal-diagonal $EC, AC$ berpotongan di $BD$ masing-masing di titik $L, K$. $BC=\sqrt{10}$. Jika titik-titik $A, K, L, E$ semuanya berada pada lingkaran $\Gamma$, tentukan panjang garis singgung dari $C$ ke $\Gamma$.
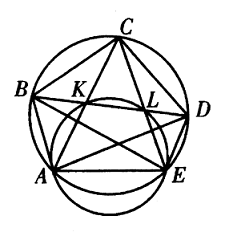
Solusi: Misalkan panjang garis singgung dari $C$ ke lingkaran $\Gamma$ adalah $a$. Maka $$\angle BKA=\frac{1}{2}(\widehat{AB}+\widehat{CD}) \text{ dan}$$ $$\angle BKA=\angle CEA=\frac{1}{2}(\widehat{AB}+\widehat{BC})$$ menyiratkan bahwa $\widehat{BC}=\widehat{CD}$. Oleh karena itu $\angle CBK=\angle BAC$, maka $\Delta BCK\sim \Delta ACB$ memberikan $$\frac{CK}{CB}=\frac{CB}{AC}\Rightarrow CK\cdot CA=CB^2.$$ Kekuatan $C$ ke $\Gamma$ memberikan $CK\cdot CA=a^2$, maka $$a=BC=\sqrt{10}.$$ - $O$ adalah pusat lingkaran segi empat cembung $ABCD$. Diketahui $AC\neq BD$, $AC$ dan $BD$ berpotongan di titik $E$. Jika $P$ adalah titik interior segi empat $ABCD$ sehingga $\angle PAB+\angle PCB=\angle PBC+\angle PDC=90^o$, buktikan bahwa $O,P.E$ kolinear.
Solusi: Misalkan lingkaran luar segi empat $ABCD$, $\Delta APC$, dan $\Delta BPD$ berturut-turut adalah $\Gamma, \Gamma_1$, dan $\Gamma_2$, maka sumbu radikal $\Gamma$ dan $\Gamma_1$ adalah garis $AC$, dan sumbu radikal $\Gamma$ dan $\Gamma_2$ adalah garis $BD$.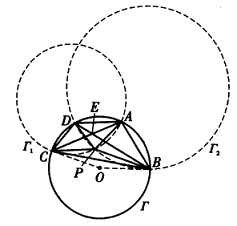
Karena $P$ berada pada $\Gamma_1$ dan $\Gamma_2$, maka $P$ berada pada sumbu radikal $\Gamma_1$ dan $\Gamma_2$. Karena $BD$ dan $AC$ berpotongan di $E$, maka $E$ adalah pusat radikal $\Gamma,\Gamma_1$ dan $\Gamma_2$, sehingga garis $PE$ adalah sumbu radikal $\Gamma_1$ dan $\Gamma_2$.
Cukuplah untuk menunjukkan bahwa $O$ memiliki daya yang sama terhadap $\Gamma_1$ dan $\Gamma_2$. Untuk catatan ini bahwa $$\angle APC=\angle PAB+\angle PCB+\angle ABC=90^o+\frac{1}{2}\angle AOC,$$ $$\angle ACO=\frac{1}{2}(180^o-\angle AOC)=180^o-\left(90^o+\frac{1}{2}\angle AOC\right)$$ $$=180^o-\angle APC=\angle ACP+\angle CAP,$$ oleh karena itu $\angle PCO=\angle CAP$, yaitu $OC$ garis singgung $\Gamma_1$ di $C$. Demikian pula, $OB$ garis singgung pada $\Gamma_2$ di $B$. Maka $OC=OB$ menyiratkan bahwa $O$ mempunyai kekuatan yang sama dengan $\Gamma_1$ dan $\Gamma_2$, maka kesimpulannya terbukti. - Pada diagram yang diberikan, $PA, PB$ adalah dua garis singgung lingkaran $☉O$ di $A$ dan $B$. Garis yang melalui $P$ memotong $☉O$ di $C$ dan $D$ dan memotong tali busur $AB$ di $Q$. Buktikan bahwa $$PQ^2=PC\cdot PD-QC\cdot QD.$$
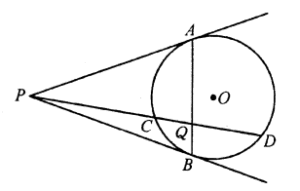
Solusi: Hubungkan $OA,OB,OP$. Misalkan titik potong $OP$ dan $AB$ adalah $H$, titik tengah $CD$ adalah $M$, hubungkan $OM$. Maka $OM\bot CD$ dan $OH\bot AB$. Oleh karena itu, $Q, H, O, M$ adalah konsiklik, sehingga $$PQ\cdot PM=PH\cdot PO.$$ Dengan menerapkan teorema proyeksi pada $\text{Rt}\Delta APO$, $$PA^2=PH\cdot PO\Rightarrow PA^2=PQ\cdot PM.$$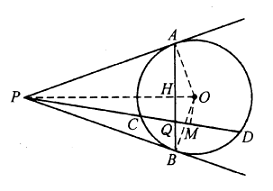
Dengan mempertimbangkan kekuatan titik $P$ terhadap lingkaran $☉O$, maka dapat disimpulkan bahwa $$PQ\cdot PM=PA^2=PC\cdot PD,$$ oleh karena itu $$PQ(PQ+QM)=PC\cdot PD,\text{ sehingga }PQ^2=PC\cdot PD-PQ\cdot QM.$$ Karena $P,A,O,M$ dan $P,B,M,O$ keduanya konsiklik, maka $P,B,M,O,A$ juga konsiklik. Dengan mempertimbangkan kekuatan $Q$ terhadap lingkaran dan $☉O$, maka diperoleh bahwa $$PQ\cdot QM=QA\cdot QB=QC\cdot QD$$ maka $A,C,B,D$ konsiklik. Jadi, $PQ^2=PC\cdot PD-QC\cdot QD$. - Bila jari-jari luar dan jari-jari dalam $\Delta ABC$ masing-masing adalah $R$ dan $r$, dan $d$ adalah jarak antara pusat lingkaran dan pusat lingkaran, maka $$d^2=R(R-2r),\text{ atau }d=\sqrt{R(R-2r)}.$$ Konsekuensi: $R\le 2r$, dan $R=2r$ jika dan hanya jika $\Delta ABC$ sama sisi.
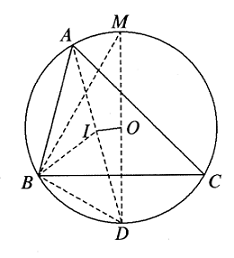
Solusi: Seperti yang ditunjukkan pada gambar, misalkan $O$ dan $I$ menjadi pusat lingkaran dan pusat $\Delta ABC$. Misalkan perpanjangan $AI$ memotong $☉O$ di $D$. Maka $D$ titik tengah dari busur $\widehat{BC}$. Tulis $$\alpha =\frac{1}{2}\angle A,\text{ }\beta=\frac{1}{2}\angle B,$$ maka $\angle IBD=\angle IBC+\angle CBD=\beta +\alpha=\angle IBA+\angle BAL=\angle BID$, oleh karena itu $\Delta DBI$ adalah sama kaki dengan $DI=DB$. Dengan mempertimbangkan kekuatan dari $I$ dan aturan sinus, maka diperoleh bahwa $$R^2-d^2=DI\cdot IA=2R\sin \alpha\cdot \frac{r}{\sin \alpha}=2Rr,$$ sehingga $d^2=R^2-2Rr=R(R-2r)$, seperti yang diinginkan. Konsekuensinya jelas. - Dua lingkaran $\Gamma_1$ dan $\Gamma_2$ memotong $A$ dan $B$, seperti yang ditunjukkan pada gambar. Sebuah garis melalui $B$ memotong $\Gamma_1$ dan $\Gamma_2$ di $C$ dan $D$, dan garis lain melalui $B$ memotong $\Gamma_1$ dan $\Gamma_2$ di $E$ dan $F$. Garis $CF$ memotong $\Gamma_1$ dan $\Gamma_2$ di $P$ dan $Q$.
Misalkan $M$ dan $N$ menjadi titik tengah pada busur $\widehat{PB}$ dan $\widehat{QB}$. Buktikan bahwa $C,F,M,N$ konsiklik jika $CD=EF$.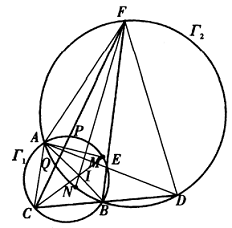
Solusi: Hubungkan $AC,AD,AE,AF,DF,CM,FN,AB$. Maka $$\angle ADB=\angle AFB,\angle ACB=\angle AEF,CD=EF$$ $$\Rightarrow \Delta ACD\sim \Delta AEF\Rightarrow AD=AF$$ $$\Rightarrow \angle ADF=\angle AFD$$ $$\Rightarrow \angle ABC=\angle AFD=\angle ADF=\angle ABF$$ $$\Rightarrow AB\text{ membagi dua sudut }\angle CBF$$ Karena $\widehat{PM}=\widehat{MB}$, maka $CM$ membagi dua sudut $\angle DCF$ dan demikian pula $FN$ membagi dua sudut $\angle CFB$. Oleh karena itu, $BA,CM,FN$ bersamaan di pusat $I$ pada $\Delta CFB$.
Mengingat kekuatan titik $I$ terhadap lingkaran $\Gamma_1$ dan $\Gamma_2$, maka $$CI\cdot IM=AI\cdot IB=NI\cdot IF,$$ maka $C,F,M,N$ konsiklik. - Misalkan lingkaran-lingkaran $\Gamma_1,\Gamma_2,\Gamma_3$ yang tidak bertumpang tindih dan saling eksternal diberikan pada bidang tersebut. Untuk setiap titik $P$ pada bidang tersebut, di luar ketiga lingkaran, konstruksikan enam titik $A_1,B_1,A_2,B_2,A_3,B_3$ sebagai berikut: Untuk setiap $i=1,2,3,A_i,B_i$ terdapat titik-titik berbeda pada lingkaran $\Gamma_i$ sehingga garis $PA_i$ dan $PB_i$ keduanya merupakan garis singgung $\Gamma_i$. Sebut titik $P$ sebagai titik luar biasa jika, dari konstruksi tersebut, tiga garis $A_1B_1,A_2B_2,A_3B_3$ konkuren. Tunjukkan bahwa setiap titik luar biasa pada bidang tersebut, jika ada, terletak pada lingkaran yang sama.
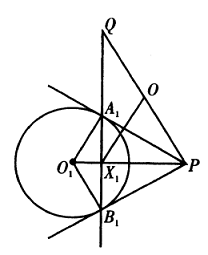
Solusi: Misalkan $O_i$ menjadi pusat dan $r_i$ jari-jari lingkaran $\Gamma_i$ untuk setiap $i=1,2,3$. Misalkan $P$ merupakan titik luar biasa, dan misalkan tiga garis $A_1B_1,A_2B_2,A_3B_3$ yang bersesuaian bertemu di $Q$. Buatlah lingkaran dengan diameter $PQ$. Sebut lingkaran tersebut $\Gamma$, dengan pusatnya $O$ dan jari-jarinya $r$. Sekarang kita nyatakan bahwa semua titik luar biasa terletak di $\Gamma$.
Misalkan $PO_1$ memotong $A_1B_1$ dalam $X_1$. Sebagai $PO_1\bot A_1B_1$, kita melihat bahwa $X_1$ terletak pada $\Gamma$. Karena $PA_1$ adalah garis singgung $\Gamma_1$, segitiga $PA_1O_1$ adalah siku-siku dan sama dengan segitiga $A_1X_1O_1$. Maka diperoleh bahwa $$\frac{O_1X_1}{O_1A_1}=\frac{O_1A_1}{O_1P},\text{ yaitu }O_1X_1\cdot O_1P=O_1A_1^2=r_1^2.$$ Di sisi lain, $O_1X_1\cdot O_1P$ juga merupakan kekuatan $O_1$ terhadap $\Gamma$, sehingga $$r_1^2=O_1X_1\cdot O_1P=(O_1O-r)(O_1O+r)=O_1O^2-r^2,\text{ }\text{ }\text{ }(✱)$$ dan karena $$r^2=OO_1^2-r_1^2=(OO_1-r)(OO_1+r).$$ Dengan demikian, $r^2$ adalah pangkat $O$ terhadap $\Gamma_1$. Dengan demikian, $r^2$ juga merupakan pangkat $O$ terhadap $\Gamma_2$ dan $\Gamma_3$. Oleh karena itu, $O$ pastilah pusat radikal dari ketiga lingkaran yang diberikan. Karena $r$, sebagai akar pangkat $O$ terhadap ketiga lingkaran yang diberikan, tidak bergantung pada $P$, maka semua titik luar biasa terletak pada $\Gamma$.
Catatan. Jika titik radikal berada pada tak terhingga (dan karenanya ketiga sumbu radikal sejajar), tidak ada titik luar biasa pada bidang tersebut, yang konsisten dengan pernyataan masalah. - Diberikan lingkaran $\omega_1$ dan $\omega_2$ yang berpotongan di titik $X$ dan $Y$, misalkan $\mathscr{l}_1$ adalah garis yang melalui pusat $\omega_1$ yang berpotongan dengan $\omega_2$ di titik $P$ dan $Q$ dan misalkan $\mathscr{l}_2$ adalah garis yang melalui pusat $\omega_2$ yang berpotongan dengan $\omega_1$ di titik $R$ dan $S$. Buktikan bahwa jika $P,Q,R$ dan $S$ terletak pada sebuah lingkaran maka pusat lingkaran ini terletak pada garis $XY$.
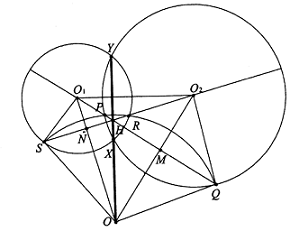
Solusi: Misalkan $\omega$ menyatakan lingkaran luar $P,Q,R,S$ dan misalkan $O$ menyatakan pusat $\omega$. Garis $XY$ adalah sumbu radikal lingkaran $\omega_1$ dan $\omega_2$. Cukup untuk menunjukkan bahwa $O$ memiliki pangkat yang sama dengan lingkaran-lingkaran tersebut; yaitu, untuk menunjukkan bahwa $$OO_1^2-O_1S^2-OO_2^2-O_2Q^2\text{ atau }OO_1^2+O_2Q^2=OO_2^2+O_1S^2.$$ Misalkan $M$ dan $N$ merupakan perpotongan garis $O_2O,\mathscr{l}_1$ dan $O_1O,\mathscr{l}_2$. Karena lingkaran $\omega$ dan $\omega_2$ berpotongan di titik $P$ dan $Q$, maka kita peroleh $PQ\bot OO_2$ (atau $\mathscr{l}_1\bot OO_2$), Maka $$OO_1^2-OQ^2=(OM^2+MO_1^2)-(OM^2+MQ^2)$$ $$=(O_2M^2+MO_1^2)-(O_2M^2+MQ^2)=O_2O_1^2-O_2Q^2$$ atau $$O_2O_1^2+OQ^2=OO_1^2+O_2Q^2.$$ Demikian pula, kita punya $O_2O_1^2+OS^2=OO_2^2+O_1S^2$. Karena $OS=OQ$, kita peroleh bahwa $OO_1^2+O_2Q^2=OO_2^2+O_1S^2$, yang mana yang harus dibuktikan.
“The function of leadership is to produce more leaders, not more followers.”
