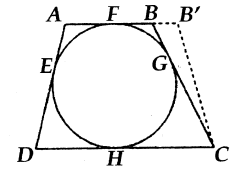
misalkan segi empat tersebut memiliki lingkaran dalam, dan $E, F, G, H$ masing-masing adalah titik singgung lingkaran pada sisi $DA, AB, BC,$ dan $CD$. Maka, $AE=AF, BF=BG=CG=CH,$ dan $DH=DE$ menyiratkan bahwa $$AB+CD=AF+BF+CH+DH$$ $$=AE+BG+CG+DE$$ $$=(AE+DE)+(BG+CG)$$ $$=AD+BC$$ Sebaliknya, jika misalkan segi empat $ABCD$ memenuhi syarat $AB+CD=BC+AD$, maka selalu mungkin untuk membuat lingkaran sedemikian rupa sehingga menyinggung sisi $AB,CD$, dan $AD$ di beberapa titik $E,F,H$ pada $AD,AB,CD$ berturut-turut.
Jika $CB$ tidak bersinggungan dengan lingkaran, buatlah garis singgung kedua dari $C$ ke lingkaran. Misalkan garis singgung tersebut memotong garis $AB$ di suatu titik $B’$, di mana $B\neq B’$. Dari penalaran di atas dapat disimpulkan bahwa $$AB’+CD=B’C+AD.$$ Maka $$AB+CD=BC+AD\Rightarrow |AB-AB’|=|BC-B’C|\Rightarrow BB’=|BC-B’C|.$$ Namun, penerapan pertidaksamaan segitiga pada $\Delta BB’C$ menunjukkan bahwa hal tersebut mustahil. Oleh karena itu, $B$ dan $B$ harus berimpit, yaitu $CB$ harus merupakan garis singgung lingkaran, yaitu, lingkaran tersebut merupakan lingkaran dalam $ABCD$.
Jika jajargenjang $ABCD$ memiliki lingkaran dalam, maka $AB=CD, BC=AD$ dan $2AB=AB+CD=BC+AD=2BC,$ sehingga $AB=BC=CD=AD,$ artinya $ABCD$ merupakan belah ketupat. Sebaliknya, jika $ABCD$ merupakan belah ketupat, kesimpulannya jelas dari penalaran di atas.

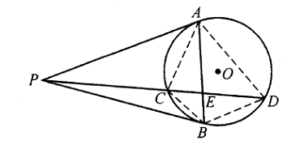
Solusi: Hubungkan $AC,AD,BC$ dan $BD$. Maka $\frac{PC}{PD}=\frac{[PAC]}{[PAD]}=\frac{[PBC]}{[PBD]}$. Dengan teorema segmen alternatif, $$\angle PAC=\angle PDA\Rightarrow \Delta PAC\sim\Delta PDA$$ dan $$\angle PBC=\angle PDB\Rightarrow \Delta PBC\sim \Delta PDB,$$ oleh karena itu $$\frac{[PAC]}{[PAD]}=\frac{AC^2}{AD^2},\frac{[PBC]}{PBD]}=\frac{BC^2}{BD^2}$$ Maka, $$\frac{AC}{AD}=\frac{BC}{BD}$$ dan $$\frac{PC}{PD}=\frac{AC^2}{AD^2}=\frac{AC}{AD}\cdot \frac{BC}{BD}.\text{ }\text{ }\text{ }\text{ }\text{ }(11.1)$$ Karena $\Delta ACE\sim\Delta DBE$ dan $\Delta BCE\sim\Delta DAE$, $$\frac{AC}{DB}=\frac{AE}{DE}\text{ dan }\frac{BC}{DA}=\frac{CE}{AE}.\text{ }\text{ }\text{ }\text{ }\text{ }(11.2)$$ Maka, kombinasi dari (11.1) dan (11.2) memberikan $$\frac{PC}{PD}=\frac{AC}{AD}\cdot\frac{BC}{BD}=\frac{AC}{DB}\cdot \frac{BC}{DA}=\frac{AE}{DE}\cdot\frac{CE}{AE}=\frac{CE}{DE},$$ seperti yang diinginkan.

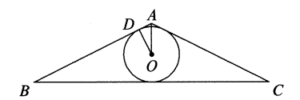
Solusi: Misalkan $BC=a,CA=b,AB=c,OD\bot AB$ di $D$, maka $$b+c-a=2AD\Rightarrow AD=\frac{b+c-a}{2}.$$ Misalkan $x=\tan\frac{A}{2}$. Karena $-\frac{4}{3}=\frac{2x}{1-x^2}\Rightarrow 2x^2-3x-2=0$, maka $$2x^2-3x-2=0\Leftrightarrow (2x+1)(x-2)=0\Rightarrow x=2(∵x>0),$$ oleh karena itu $2=DO=\tan \frac{A}{2}\cdot AD=2AD\Rightarrow AD=1\Rightarrow b+c-a=2$. Karena $$\tan A=-\frac{4}{3}\Rightarrow \sin A=\frac{4}{5},\cos A=-\frac{3}{5},$$ maka $a+b+c=\frac{a+b+c}{2}\cdot 2=[ABC]=\frac{1}{2}bc\sin A=\frac{2}{5}bc$. Dari $$a+b+c=2(b+c)-(b+c-a)=2(b+c)-2$$ diperoleh bahwa $bc=5(b+c)-5\ge 10\sqrt{bc}-5$, yaitu $(\sqrt{bc})^2-10\sqrt{bc}+5\ge 0$. Oleh karena itu $$\sqrt{bc}\ge \frac{10+\sqrt{80}}{2}=5+2\sqrt{5},\text{ atau }bc\ge 45+20\sqrt{5}.$$ Maka, $[ABC]=\frac{2}{5}bc\ge 18+8\sqrt{5}$, dan persamaan berlaku ketika $b=c=5+2\sqrt{5}$.

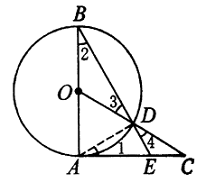
Solusi: Hubungkan $AD$. Maka $AD$ adalah ketinggian $\text{Rt}\Delta ABE$ pada $BE$. Dari $\Delta ADE\sim\Delta BDA$, $$\frac{AE}{DE}=\frac{AB}{AD}=\frac{AC}{AD}.$$ Dengan teorema segmen alternatif, $\angle 1=\angle 2$. $OB=OD$ menyiratkan $\angle 2=\angle 3$, maka $\angle 1=\angle 2=\angle 3=\angle 4$, oleh karena itu $\Delta CDE\sim\Delta CAD$. Maka $$\frac{AC}{AD}=\frac{CD}{DE}$$ Oleh karena itu $\frac{AE}{DE}=\frac{CD}{DE}$, yaitu $AE=CD$.
$\Delta CDE\sim\Delta CAD$ menyiratkan juga $\frac{CD}{AC}=\frac{CE}{CD}$, yaitu $CD^2=CE\cdot AC$, oleh karena itu $$AE^2=CE\cdot AC.$$ Misalkan $AE=x$, maka $CE=a-x$ dan $x^2=a(a-x)$ yang memberikan $x^2+ax-a^2=0$, jadi $$AE=x=\frac{-a+\sqrt{a^2+4a^2}}{2}=\frac{\sqrt{5}-1}{2}a \text{ (akar negatif tidak dapat diterima)}.$$

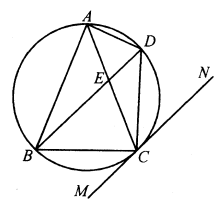
(i)     Buktikan bahwa $\Delta ABE\cong \Delta ACD;$
(ii)    Tentukan $AE$ jika $AB=6,BC=4$.
Solusi: 
(i)     Untuk segitiga $ABE$ dan $ACD$, karena $AB=AC,\angle ABE=\angle ACD$ dan dengan teoream segmen alternatif dan $BD||MN$, $$\angle CAD=\angle NCD=\angle BDC=\angle BAC=\angle BAE,$$ oleh karena itu $\Delta ABE\cong \Delta ACD$ (S.A.A.).
(ii)    Maka $$\angle BAC=\angle CAD,BE=CD\Rightarrow \angle BDC=\angle CBD,BE=CD$$ $$\Rightarrow BE=CD=BC=4.$$ Misalkan $AE=x$. Maka $\Delta AEB\sim\Delta DEC$ menyiratkan bahwa $$DE=AE\cdot \frac{CD}{AB}=\frac{4x}{6}=\frac{2x}{3}.$$ Teorema tali busur berpotongan menghasilkan $x(6-x)=4\cdot \frac{2x}{3}$, maka diperoleh $$x=6-\frac{8}{3}=\frac{10}{3}.$$ Maka, $AE=\frac{10}{3}$.

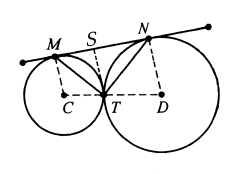
Solusi: Seperti yang ditunjukkan pada diagram, misalkan jari-jari $⊙C$ dan $⊙D$ masing-masing adalah $2$ dan $3$, dan misalkan $\angle MCT =\theta$, maka $\angle NDT=\pi-\theta$. Berdasarkan teorema segmen alternatif, $$\angle NMT=\frac{1}{2}\theta,\angle MNT=\frac{1}{2}(\pi-\theta).$$ Oleh karena itu $\angle MTN=\frac{\pi}{2}$. Dari $T$ masukkan $TS\bot MN$ pada $S$, maka $TS$ adalah tinggi pada sisi miring $\text{Rt}\Delta MTN$. Berdasarkan teorema proyeksi segitiga siku-siku, $$\frac{MT^2}{NT^2}=\frac{MS\cdot MN}{NS\cdot NM}=\frac{MS}{NS}=\frac{CT}{DT}=\frac{2}{3}\Rightarrow \frac{MT}{NT}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}.$$

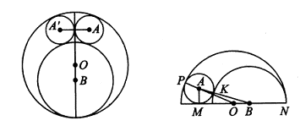
Solusi: Berdasarkan simetri, pusat $O$ dan $B$ berada pada garis singgung persekutuan dalam dari $⊙A$ dan $⊙A’$, jadi cukup untuk mempertimbangkan setengah dari grafik, seperti yang ditunjukkan pada diagram kanan di atas. 
Misalkan $MO=x,MB=y$, maka $MN=x+R=y+2r$, maka $x=y+2r-R$. Karena $AO=R-r,AB=3r$, dengan teorema Pythagoras, $$y^2=MB^2=AB^2-AM^2=8r^2\Rightarrow y=\sqrt{8}r,x=(2+\sqrt{8})r-R.$$ $$x^2=MO^2=AO^2-AM^2=(R-r)^2-r^2=R^2-2Rr,$$ maka $[(2+\sqrt{8})r-R]^2=R^2-2Rr$, yang memberikan $(2+2\sqrt{8})R=(2+\sqrt{8})^2r$, maka $$\frac{r}{R}=\frac{2+2\sqrt{8}}{(2+\sqrt{8})^2}=\frac{1+2\sqrt{2}}{2(\sqrt{2}+1)^2}$$ $$=\frac{(1+2\sqrt{2})(\sqrt{2}-1)^2}{2}=\frac{4\sqrt{2}-5}{2}.$$