Hukum Sinus dan Hukum Kosinus

Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Definisi
- Contoh Soal
Definisi
- Hukum Sinus (atau disebut sebagai Aturan Sinus singkatnya): Dalam setiap segitiga $ABC$ dengan sudut dalam $\angle A,\angle B$ dan $\angle C$, selalu benar bahwa $$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C},$$ dimana $a,b,c$ adalah tiga sisi panjang $BC,CA,AB$ masing-masing. Lebih lanjut, aturan sinus yang diperluas selalu benar: $$a=2R\sin A, \text{ }\text{ }b=2R\sin B,\text{ }\text{ }c=2R\sin C,$$ dimana $R$ adalah jari-jari lingkaran luar $\Delta ABC$.
Bukti:
(i) Ketika $\angle A$ lancip, seperti yang ditunjukkan pada gambar (1), $$a=2R\sin A’=2R\sin A.$$
(ii) Ketika $\angle A$ tumpul, seperti yang ditunjukkan pada gambar (2), maka $$a=2R\sin A’=2r\sin(\pi – A)=2R\sin A.$$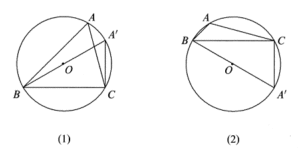
- Hukum Kosinus (atau disebut sebagai Aturan Kosinus singkatnya): Dalam setiap segitiga $ABC$ dengan sudut dalam $\angle A,\angle B$ dan $\angle C$, selalu benar bahwa $$a^2=b^2+c^2-2bc\cos A,b^2=c^2+a^2-2ca \cos B,c^2=a^2+b^2-2ab\cos C,$$ dimana $a,b,c$ adalah tiga sisi panjang $BC,CA,AB$ masing-masing.
Bukti: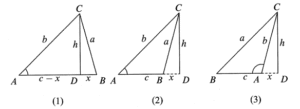
(i) Ketika $\angle A$ lancip, seperti yang ditunjukkan pada gambar (1) atau (2), maka $$a^2=h^2+x^2=(b\sin A)^2+(c-b\cos A)^2$$ $$=b^2\sin^2 A+c^2+b^2\cos^2 A-2bc\cos A$$ $$=b^2+c^2-2bc \cos A$$
(ii) Ketika $\angle A$ sudut tumpul, seperti yang ditunjukkan pada gambar (3), $$a^2=h^2+(c+x)^2=(b\sin A)^2+(c-b\cos A)^2=b^2+c^2-2bc\cos A.$$ Aturan kosinus dapat dinyatakan dalam bentuk $$\cos A=\frac{b^2+c^2-a^2}{2bc},\cos B=\frac{c^2+a^2-b^2}{2ca},\cos C=\frac{a^2+b^2-c^2}{2ab},$$ maka aturan kosinus berarti bahwa sudut-sudut dalam suatu segitiga ditentukan oleh panjang ketiga sisinya.
Teorema berikut memiliki aplikasi yang luas, dan dapat dibuktikan dengan menerapkan aturan kosinus.
Teorema I. (Teorema Stewart) Untuk segitiga $ABC$, jika $D$ adalah sebuah titik pada ruas garis $BC$ sehingga $BD=p,CD=q$, maka $$AD^2=\frac{b^2p+c^2q}{p+q}-pq.$$
Bukti:
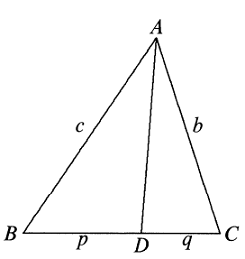
Seperti yang ditunjukkan pada gambar, menerapkan aturan kosinus pada $\Delta ABD$ dan $\Delta ABC$ memberikan $$\frac{c^2+p^2-AD^2}{2pc}=\cos B=\frac{a^2+c^2-b^2}{2ac}.$$ Perhatikan bahwa $a=BC=p+q$, oleh karena itu $$AD^2=c^2+p^2+\frac{b^2p-c^2p}{a}-pa$$ $$=\frac{(p+q)c^2+b^2p-pc^2}{a}+p^2-(p+q)p$$ $$=\frac{b^2p+c^2q}{p+q}-pq$$
Contoh Soal
- Ketika $AD$ adalah median pada sisi $BC$ dari $\Delta ABC$, maka $$AD=\frac{1}{2}\sqrt{2b^2+2c^2-a^2}.$$
Solusi: Menerapkan teorema Stewart pada kasus $p=q=\frac{1}{2}a$ diperoleh $$AD^2=\frac{\frac{1}{2}a}{a}(b^2+c^2)-\frac{1}{4}a^2=\frac{1}{4}(2b^2+2c^2-a^2).$$ Oleh karena itu $AD=\frac{1}{2}\sqrt{2bc^2+2c^2-a^2}$. - (Rumus untuk garis bagi sudut) Pada $\Delta ABC$ ketika $AD$ adalah garis bagi sudut dari $\angle A$, maka $$AD=\frac{2}{b+c}\sqrt{bcs(s-a)},$$ dimana $s$ adalah setengah keliling dari $\Delta ABC$, yaitu $s=\frac{1}{2}(a+b+c)$.
Solusi: MIsalkan $BD=p,DC=q$. Teoema garis bagi sudut memberikan $\frac{p}{q}=\frac{c}{b}$, maka $$p=\frac{ac}{b+c}\text{ dan }q=\frac{ab}{b+c}.$$ Maka penerapan teorema Stewart memberikan $$AD^2=\frac{b^2ac+c^2ab}{a(b+c)}-\frac{a^2bc}{(b+c)^2}=bc-\frac{a^2bc}{(b+c)^2}=\frac{bc[(b+c)^2-a^2]}{(b+c)^2}$$ $$=\frac{bc(b+c-a)(b+c+a)}{(b+c)^2}=\frac{4bc(s-a)s}{(b+c)^2}.$$ Oleh karena itu $AD=\frac{2}{b+c}\sqrt{bcs(s-a)}$. - (Rumus Heron) Luas $\Delta ABC$, dinyatakan dengan $[ABC]$, diberikan oleh $$[ABC]=\sqrt{s(s-a)(s-b)(s-c)},$$ dimana $s=\frac{1}{2}(a+b+c)$.
Solusi: Cukup mencari tinggi $h$ pada $BC$. Misalkan $AD\bot BC$ di $D$, dimana $D$ adalah ruas garis $BC$, maka $$c^2-p^2=h^2=b^2-q^2\Rightarrow c^2-b^2=p^2-q^2\Rightarrow p-q=\frac{c^2-b^2}{a}.$$ Hubungkan dengan $p+q=a$, maka diperoleh $$p=\frac{1}{2}\left[\frac{c^2-b^2}{a}+a\right]=\frac{c^2+a^2-b^2}{2a},$$ $$q=\frac{1}{2}\left[a-\frac{c^2-b^2}{a}\right]=\frac{a^2+b^2-c^2}{2a},$$ maka penerapan teorema Stewart memberikan $$h^2=c^2-p^2=\frac{4a^2c^2-(c^2+a^2-b^2)^2}{4a^2}$$ $$=\frac{(2ac-c^2-a^2+b^2)(2ac+c^2+a^2-b^2)}{4a^2}$$ $$=\frac{1}{4a^2}[b^2-(c-a)^2]\cdot [(c+a)^2-b^2]$$ $$=\frac{1}{4a^2}(b-a+c)(b+a-c)(a+c-b)(a+c+b)$$ $$=\frac{4(s-a)(s-c)(s-b)s}{a^2}.$$ Oleh karena itu $$h=\frac{2}{a}\sqrt{s(s-a)(s-b)(s-c)}\text{ dan }[ABC]=\sqrt{s(s-a)(s-b)(s-c)}.$$ Catatan: Dalam pembuktian Rumus Heron di atas, diasumsikan bahwa $D$ berada pada ruas garis $BC$, tetapi mudah dilihat bahwa rumus tersebut masih berlaku untuk semua segitiga tumpul. - Diketahui $\frac{\sin a}{\sin b}=\frac{\sin c}{\sin d}=\frac{\sin (a-c)}{\sin (b-d)}$, dimana $a,b,c,d \in (0,\pi)$. Buktikan bahwa $a=b,c=d$.
Solusi: Karena $a=c$ menyiratkan bahwa $a=c=0$, tetapi ini tidak mungkin, maka $a\neq c$. Misalkan $a>c$, maka persamaan yang diberikan menyiratkan bahwa $b>d$, dan $$\frac{\sin (\pi-a)}{\sin(\pi -b)}=\frac{\sin c}{\sin d}=\frac{\sin(a-c)}{\sin(b-d)}.$$ Misalkan $\Delta ABC$ memenuhi $\angle A=\pi -a ,\angle B=c,\angle C=a-c$, dan $\Delta DEF$ memenuhi $\angle D=\pi -b,\angle E=d,\angle F=b-d$. Karena $\frac{\sin A}{\sin D}=\frac{\sin B}{\sin E}=\frac{\sin C}{\sin F}$, dengan aturan sinus diperoleh bahwa $$\frac{BC}{EF}=\frac{AC}{DF}=\frac{AB}{DE},$$ oleh karena itu $\Delta ABC \sim \Delta DEF,\angle A=\angle D,\angle B=\angle E$, yaitu $a=b,c=d$. - Jika panjang $a,b,c$ dari tiga sisi $\Delta ABC$ memenuhi $2b=a+c$, temukan nilai dari $5\cos A-4\cos A\cos C+5\cos C$.
Solusi: Dengan aturan sinus, hubungan $2b=a+c$ menyiratkan bahwa $2\sin B=\sin A+\sin C$. Maka $$\sin(A+C)=\frac{\sin A+\sin C}{2}$$ $$\Rightarrow 2\sin \frac{A+C}{2}\cos \frac{A+C}{2}=\sin \frac{A+C}{2}\cos \frac{A-C}{2}$$ $$\Rightarrow 2\cos\frac{A+C}{2}=\cos \frac{A-C}{2}.$$ Oleh karena itu $$5\cos A-4 \cos A\cos C+5\cos C=5(\cos A+\cos C)-4\cos A\cos C$$ $$=10\cos \frac{A+C}{2}\cos \frac{A-C}{2}-2[\cos(A+C)+\cos (A-C)]$$ $$=10\cos \frac{A+C}{2}\cos \frac{A-C}{2}-4[\cos^2\frac{A+C}{2}+\cos^2\frac{A-C}{2}-1]$$ $$=20\cos^2 \frac{A+C}{2}-4[\cos^2\frac{A+C}{2}+4\cos^2\frac{A+C}{2}-1]=4.$$ Catatan: Dalam pembuktiannya, penerapan aturan sinus untuk mengubah hubungan antara sisi-sisi menjadi hubungan antara sudut-sudut memegang peranan penting. - Buktikan bahwa pertidaksamaan $$\frac{\cos A}{a^3}+\frac{\cos B}{b^3}+\frac{\cos C}{c^3}\ge \frac{3}{2abc}$$ berlaku untuk segitiga $ABC$ mana pun, di mana $a, b, c$ adalah panjang tiga sisi, dan $\angle A,\angle B,\angle C$ masing-masing adalah sudut dalam yang berhadapan.
Solusi: Aturan kosinus dan ketidaksamaan $x+\frac{1}{x}\ge 2$ untuk $x>0$ memberikan $$\frac{\cos A}{a^3}+\frac{\cos B}{b^3}+\frac{\cos C}{c^3}=\frac{b^2+c^2-a^2}{2a^3bc}+\frac{a^2+c^2-b^2}{2b^3ca}+\frac{a^2+b^2-c^2}{2c^3ab}$$ $$=\frac{1}{2abc}\left\{\left[\left(\frac{a}{b}\right)^2+\left(\frac{b}{a}\right)^2\right]+\left[\left(\frac{b}{c}\right)^2+\left(\frac{c}{b}\right)^2\right]+\left[\left(\frac{c}{a}\right)^2+\left(\frac{a}{c}\right)^2\right]-3\right\}$$ $$\ge \frac{1}{2abc}(2+2+2-3)=\frac{3}{2abc}.$$ - Misalkan $a,b,c$ adalah panjang tiga sisi $\Delta ABC$, dan $b^2=ac$. Jika $\angle B=x$ dan $f(x)=\sin\left(4x-\frac{x}{6}\right)-\frac{1}{2}$, tentukan range dari $f(x)$.
Solusi: Aturan kosinus memberikan $$\cos x=\frac{a^2+c^2-b^2}{2ac}\ge \frac{2ac-ac}{2ac}=\frac{1}{2}.$$ Karena $0<x<\pi$, maka $0<x\le \frac{\pi}{3}$ dan $-\frac{\pi}{6}<4x-\frac{\pi}{6}\le \frac{7\pi}{6}$. Oleh karena itu $-\frac{1}{2}\le \sin\left(4x-\frac{x}{6}\right)\le 1$$ dan range dari $f(x)$ adalah $\left[-1,\frac{1}{2}\right]$. - Diketahui dalam $\Delta ABC$, $a\cos A=b\cos B$. Tentukan bentuk dari $\Delta ABC$.
Solusi: Dengan aturan kosinus, $$a\cos A=b\cos B\Leftrightarrow a\cdot \frac{b^2+c^2-a^2}{2bc}=b\cdot \frac{a^2+c^2-b^2}{2ac}$$ $$\Leftrightarrow a^2(b^2+c^2-a^2)=b^2(a^2+c^2-b^2)\Leftrightarrow a^2c^2-a^4-b^2c^2+b^4=0$$ $$\Leftrightarrow (a^2-b^2)(c^2-a^2-b^2)=0\Leftrightarrow a=b\text{ atau }a^2+b^2=c^2.$$ Maka, $\Delta ABC$ adalah segitiga sama kaki atau segitiga siku-siku.
Solusi 2: Aturan sinus memberikan $2R\sin A\cos A=2R\sin B\cos B$, maka $\sin 2A=\sin 2B$. Karena $0<2A,2B<2\pi$, maka $A=B$ atau $2A=\pi-2B$. $A=B$ menyiratkan bahwa $\Delta ABC$ adalah segitiga sama kaki.
Jika $2A=\pi-2B$, maka $A+B=\frac{\pi}{2}$, jadi $C=\frac{\pi}{2}$, dengan begitu $\Delta ABC$ adalah segitiga siku-siku.
Jadi, $\Delta ABC$ adalah segitiga sama kaki atau segitiga siku-siku.
Catatan: Dalam pembuktiannya, kami fokus pada hubungan sisi-sisi dengan menggunakan aturan kosinus; dan kami fokus pada hubungan sudut dengan menggunakan aturan sinus.
Solusi dari setiap Permasalahan diberikan pada kelas online
“Change is the law of life. And those who look only to the past or present are certain to miss the future.”

