Fungsi Indikatif dan Fungsi Logaritma

- Definisi
- Operasi Dasar pada Fungsi Indisial dan Fungsi Logaritma
- Contoh Soal
Definisi
Definisi 1. Fungsi dengan bentuk $y = a^x$ disebut fungsi indikatif, di mana $a$ adalah konstanta (disebut basis) dengan $a > 0$ dan $a \neq 1$, dan $x$ adalah variabel bebas dengan rentang $(-∞, +∞)$, yaitu $\mathbb{R}$.
$y = a^x$ adalah fungsi yang meningkat secara ketat dengan domain $(-∞,+∞)$ dan rentang $(0, +∞)$ ketika $a > 1$; dan merupakan fungsi yang menurun secara ketat dengan domain $(-∞, +∞)$ dan rentang $(0, +∞)$ ketika $0 < a < 1$.
Definisi 2. Fungsi logaritma $y = \log_a x$, dengan $a > 0, a ≠ 1$ dan $x > 0$, didefinisikan sebagai fungsi invers dari fungsi indeks $y = a^x$. Jadi, domainnya adalah $(0, +∞)$ dan rentangnya adalah $(-∞, +∞)$.
Mirip dengan fungsi indikatif, $y = \log_a x$ merupakan fungsi yang meningkat secara ketat ketika $a > 1;$ dan merupakan fungsi yang menurun secara ketat ketika $0 < a < 1$.
Grafik $y = a^x$ dan grafik $y = log_a x$ merupakan simetri terhadap garis $y = x$, seperti yang ditunjukkan pada diagram berikut.
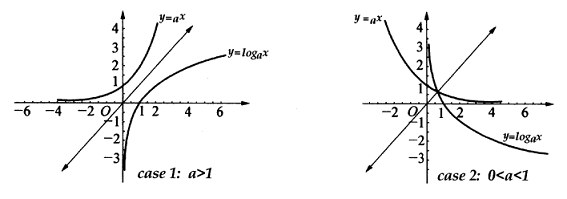
Operasi Dasar pada Fungsi Indisial dan Fungsi Logaritma
Untuk $a>0$ dan $a\neq 1$,
(i) $a^xa^y=a^{x+y};$
(ii) $(a^x)^y=a^{xy};$
(iii) $(ab)^x=a^xb^x.$
Untuk $M,N>0,m,n,\in \mathbb{R},a,b>0$ dan $a\neq 1,b\neq 1$,
(iv) identitas logaritma: $x=a^{\log_a^{\text{ }x}};$
(v) $\log_a MN=\log_a M+\log_a N;$
(vi) $\log_a \frac{M}{N}=\log_a M-\log_a N;$
(vii) $\log_a M^n=n\log_a M;$
(viii) $\log_a N=\frac{\log_b N}{\log_b a}$. Secara khusus, $\log_a b=\frac{1}{\log_b a}$.
(ix) $M^{\log_a N}=N^{\log_a M}$ untuk $M,N\neq 1$.
Contoh Soal
- Temukan bilangan asli terkecil $n$ yang memenuhi pertidaksamaan $12^{200} < n^{300}$.
Solusi: Ubah kedua sisi agar memiliki kekuatan yang sama, lalu bandingkan basisnya. $$12^{200}<n^{300}\Leftrightarrow (144)^{100}<(n^3)^{100}\Leftrightarrow 144<n^3.$$ Maka $5^3<144<6^3$ menyiratkan bahwa $n=6$. - Berapa banyak bilangan bulat $x$ yang memenuhi persamaan $(x^2-2x-4)^{x^2+3x+2}=1$?
Solusi: Untuk membahas persamaan $f(x)^{g(x)} = 1$, terdapat tiga kemungkinan kasus: (i) $g(x) = 0$ tetapi $f(x) ≠ 0;$ (ii) $f(x) = 1;$ (iii) $f(x) = -1$ dan $g(x)$ merupakan bilangan genap.
(i) Ketika $x^2+3x+2=0$ dan $x^2-2x-4\neq 0$, maka $x=-1$ atau $-2;$
(ii) Ketika $x^2-2x-4=1$, maka $x=1-\sqrt{6}$ atau $1+\sqrt{6};$
(iii) Ketika $x^2-2x-4=-1$ dan $x^2+3x+2$ adalah bilangan genap, maka $x=3$ atau $-1$.
Jadi, ada $3$ kemungkinan nilai untuk $x$. - Temukan semua bilangan real $x$ yang memenuhi persamaan $$2^x+3^x-4^x+6^x-9^x=1.$$
Solusi: Dengan menetapkan $2x = a$ dan $3x = b$, persamaan yang diberikan menjadi $$1+a^2+b^2-a-b-ab=0.$$ Mengalikan kedua sisi persamaan terakhir dengan $2$ dan melengkapi kuadrat, maka $$(1- a)^2 + (a – b)^2 + (b – 1)^2 = 0.$$ Oleh karena itu $a=b=1$, yaitu $2^x=3^x=1$. Jadi $x=0$ adalah solusi unik. - Temukan semua bilangan riil $x$ yang memenuhi $10^x + 11^x +12^x = 13^x + 14^x.$
Solusi: Mudah untuk memeriksa apakah $x = 2$ adalah solusi. Kita mengklaim bahwa itu adalah satu-satunya solusi. Faktanya, membagi dengan $13^x$ di kedua sisi menghasilkan $$\left(\frac{10}{13}\right)^x+\left(\frac{11}{13}\right)^x+\left(\frac{12}{13}\right)^x=1+\left(\frac{14}{13}\right)^x.$$ Ruas kiri merupakan fungsi x yang menurun secara ketat, dan ruas kanan merupakan fungsi $x$ yang meningkat secara ketat. Oleh karena itu, kedua kurva tersebut dapat memiliki paling banyak satu titik perpotongan. - Jumlah solusi untuk $x$ dalam persamaan $$5^{2x}-26\cdot 5^x+\sqrt{5^{2x}-26\cdot 5^x+26}=-24$$ adalah
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5.
Solusi: Substitusi $y=\sqrt{5^{2x}-26\cdot 5^x+26}$ menghasilkan $y^2+y-2=0$, oleh karena itu $y=1$. Maka $$\sqrt{5^{2x}-26\cdot 5^x+26}=1\Rightarrow (5^x-1)(5^x-25)=0\Rightarrow x_1=0\text{ }\text{ }x_2=2.$$ Jawaban nya (B). - Misalkan $a, b,$ dan $c$ adalah bilangan riil yang lebih besar dari $1$. Tentukan nilai $$\frac{1}{1+\log_{a^2b}\left(\frac{c}{a}\right)}+\frac{1}{1+\log_{b^2c}\left(\frac{a}{b}\right)}+\frac{1}{1+\log_{c^2a}\left(\frac{b}{c}\right)}$$
Solusi: Rumus untuk mengubah basis memberikan $\log_u v=\frac{1}{\log_v u}$ jika $u,v>0$ dan $u,v\neq 1$, maka $$\frac{1}{1+\log_{a^2b}\left(\frac{c}{a}\right)}+\frac{1}{1+\log_{b^2c}\left(\frac{a}{b}\right)}+\frac{1}{1+\log_{c^2a}\left(\frac{b}{c}\right)}$$ $$=\frac{1}{\log_{a^2b}(abc)}+\frac{1}{\log_{b^2c}(abc)}+\frac{1}{\log_{c^2a}(abc)}$$ $$=\log_{abc}(a^2b)(b^2c)(c^2a)=\log_{abc}(abc)^3=3.$$ - Evaluasi $5^a$, dimana $a=\frac{\log_7 4(\log_7 5-\log_7 2)}{\log_7 25(\log_7 8-\log_7 4)}$.
Solusi: Pertama-tama, kita sederhanakan indeks $a$: $$a=\frac{\log_7 4(\log_7 5-\log_7 2)}{\log_7 25(\log_7 8-\log_7 4)}=\frac{\log_7 2^2\cdot \log_7 \frac{5}{2}}{\log_7 5^2\cdot \log_7 2}=\frac{\log_7 \frac{5}{2}}{\log_7 5}=\log_5 \frac{5}{2},$$ oleh karena itu $5^a=5^{\log_5 \frac{5}{2}}=\frac{5}{2}$. - Selesaikan persamaan $x+\log_3(3^x-24)=4$.
Solusi: Persamaan yang diberikan menghasilkan $\log_3 (3^x-24)=4-x$, jadi $3^x>24$ dan $$3^x-24=3^{4-x}=\frac{81}{3^x},$$ $$(3^x)^2-24\cdot 3^x-81=0,$$ $$(3^x+3)(3^x-27)=0,$$ $$∵3^x+3>3,∴ 3^x=27=3^3,\text{ yaitu }x=3.$$ - Selesaikan persamaan $\log_{30}(x+\sqrt[3]{x})=\frac{1}{3}\log_3x$.
Solusi: Misalkan $t=\frac{1}{3}\log_3x$, maka $x=3^{3t}=27^t$ dan $$\log_{30}(27^t+3^t)=t,$$ $$27^t+3^t=30^t,$$ $$\left(\frac{9}{10}\right)^t+\left(\frac{1}{10}\right)^t=1.$$ Tentukan $f(t)=\left(\frac{9}{10}\right)^t = \left(\frac{1}{10}\right)^t,t\in \mathbb{R}$ maka $f$ adalah fungsi yang menurun secara ketat pada $\mathbb{R}$ dan $f(1) = 1$. Jadi, $t = 1$, dan karenanya $x = 27^t = 27$. - Selesaikan sistem persamaan $$\log_yx+\log_xy=\frac{5}{2},\text{ }\text{ }\text{ }(4.1)$$ $$x+y=12.\text{ }\text{ }\text{ }(4.2)$$
Solusi: Persamaan yang diberikan menyiratkan bahwa $x,y>0$ dan $x,y\neq 1$. Dari $(4.1)$ $$2(\log_xy)^2-5\log_xy+2=0,$$ $$(2\log_xy-1)(\log_xy-2)=0,$$ $$\log_xy=\frac{1}{2}\text{ atau }2\Rightarrow y=\sqrt{x}\text{ atau }x^2.$$
(i) $y=\sqrt{x}\Rightarrow 12-x=\sqrt{x}\Rightarrow \sqrt{x}=3\Rightarrow x=9,y=3;$
(ii) $y=x^2\Rightarrow 12-x=x^2\Rightarrow x=3\Rightarrow x=3,y=9.$
Jadi, ada dua solusi: $(9,3)$ dan $(3,9)$.
Solusi dari setiap Permasalahan diberikan pada kelas online
“Change is painful, but nothing is as painful as staying stuck somewhere you don’t belong.”

