Prinsip Lubang Merpati
Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Bentuk Dasar Prinsip Pigeonhole
- Contoh Soal
Bentuk Dasar Prinsip Pigeonhole
Prinsip I: Ketika $m + 1$ merpati memasuki $m$ lubang merpati ($m$ bilangan bulat positif), harus ada paling sedikit satu lubang yang dihuni lebih dari 1 merpati.
Prinsip II: Ketika $m + 1$ merpati memasuki $n$ lubang merpati, harus ada satu lubang yang berisi paling sedikit $\left\lfloor \frac{m}{n} \right\rfloor+ 1$ merpati.
Prinsip III: Ketika banyak elemen tak terhingga dipartisi menjadi himpunan terhingga, harus ada setidak nya satu himpunan yang berisi banyak elemen tak terhingga.
Prinsip Pigeonhole mudah dipahami, dan ketiga bentuk di atas dapat dibuktikan sekaligus dengan kontradiksi. Namun, bukan berarti penggunaan prinsip tersebut mudah. Prinsip Pigeonhole memiliki berbagai penerapan. Penggunaan prinsip untuk membuktikan keberadaan suatu kasus, pada dasarnya adalah mengklasifikasikan semua kasus yang mungkin ke dalam beberapa atau hanya beberapa kelas, kemudian menggunakan pembuktian dengan kontradiksi untuk menunjukkan kesimpulan yang diinginkan. Jadi, masalah utama dalam menerapkan prinsip ini adalah melakukan klasifikasi kasus-kasus yang mungkin, yaitu untuk menemukan “pigeonhole” yang berbeda namun tepat untuk berbagai permasalahan. Namun, hingga saat ini, masih belum ada metode terpadu untuk menemukan “pigeonhole”. Contoh-contoh di bawah ini akan menunjukkan beberapa metode untuk mendapatkan “pigeonhole”.
Contoh Soal
- Di dalam sebuah kantong, terdapat beberapa bola dengan ukuran yang sama yang diwarnai dengan $7$ warna, dan untuk setiap warna jumlah bolanya adalah $77$. Setidaknya, berapa banyak bola yang perlu dipilih secara acak untuk memastikan bahwa seseorang dapat memperoleh $7$ kelompok yang masing-masing terdiri dari $7$ bola sehingga dalam setiap kelompok bola-bola tersebut homokromatik?
Solusi: Untuk soal ini, wajar jika setiap warna dianggap sebagai satu lubang merpati, dan bola yang ditarik adalah seekor merpati. Pada langkah pertama, untuk mendapatkan sekelompok $7$ bola dengan warna yang sama, setidaknya $43$ bola perlu diambil dari kantong secara acak, karena jika hanya $42$ bola yang diambil, mungkin ada tepat $6$ bola untuk setiap warna. Berdasarkan prinsip lubang merpati, harus ada satu warna sehingga setidaknya $\left\lfloor 42/7 \right\rfloor +1=7$ bola yang ditarik memiliki warna ini.
Selanjutnya, setelah mendapatkan kelompok pertama, cukup mengambil $7$ bola lagi dari kantong untuk mendapatkan $43$ bola lagi. Dengan cara yang sama, kelompok kedua yang terdiri dari $7$ bola homokromatik dapat diperoleh.
Dengan mengulangi proses ini sebanyak $6$ kali, diperoleh $7$ kelompok bola homokromatik. Jadi, jumlah bola terkecil yang terambil adalah $43 + 6 × 7 = 85.$ - Sebuah kantong berisi $200$ kelereng. Ada $60$ kelereng merah, $60$ kelereng biru, $60$ kelereng hijau, dan $20$ sisanya terdiri dari kelereng kuning dan putih. Jika kelereng dipilih dari kantong tanpa melihat, berapa jumlah kelereng terkecil yang harus diambil agar setidaknya $20$ kelereng berwarna sama di antara kelereng yang dipilih?
Solusi: Ketika $77$ kelereng dipilih, kemungkinan terdapat $19$ kelereng merah, $19$ kelereng biru, $19$ kelereng hijau, dan $20$ kelereng kuning dan putih.
Jika $78$ kelereng dipilih secara acak, jumlah kelereng kuning dan putih di antara kelereng-kelereng tersebut paling banyak $20$. Oleh karena itu, terdapat setidaknya $58$ kelereng berwarna merah, biru, atau hijau. Menurut Prinsip Pigeonhole, jumlah kelereng yang terambil dengan warna tertentu tidak kurang dari $\left\lfloor \frac{57}{3} \right\rfloor+ 1 = 20$, yaitu minimal $20$. Dengan demikian, jumlah kelereng terkecil yang akan terambil adalah $78$.
Dalam soal ini, suatu warna dianggap sebagai pigeonhole, dan kemudian kelereng yang terambil dianggap sebagai merpati. - Jika $51$ angka diambil secara acak dari $100$ bilangan asli pertama $\{1, 2, . . . , 100\}$, buktikan bahwa harus ada dua angka yang ditarik sedemikian rupa sehingga salah satunya merupakan kelipatan dari yang lain.
Solusi: Misalkan $A = \{1, 2, 3, . . . , 100\}$. Terdapat total $50$ bilangan ganjil dalam himpunan $A: 2k − 1, k = 1, 2, 3, . . . , 50$. Setiap bilangan di $A$ dapat ditulis secara unik dalam bentuk $2^mq$, di mana $m$ adalah bilangan bulat non-negatif, dan $q$ adalah bilangan ganjil.
Ketika semua bilangan di $A$ dipartisi menurut $q$ menjadi $50$ kelas, maka setiap bilangan di $A$ harus termasuk dalam kelas yang unik. Sekarang, untuk setiap $51$ bilangan di $A$, berdasarkan Prinsip Pigeonhole, harus ada dua bilangan yang berasal dari kelas yang sama, dan kedua bilangan ini harus memenuhi persyaratan: satu merupakan kelipatan dari yang lain karena keduanya memiliki $q$ yang sama.
Dalam soal ini, pigeonhole adalah himpunan semua bilangan di $A$ dengan faktor ganjil maksimum yang sama, $q$, karena setiap dua bilangan di pigeonhole memiliki sifat yang diperlukan. - Tentukan jumlah maksimum elemen dari subhimpunan $L$ yang terdiri dari $\{1, 2, 3, …, 1999\}$ sehingga selisih dua elemen berbeda dari $L$ tidak sama dengan $4$.
Solusi: Misalkan $A = \{1, 2, 3, · · · , 1999\}$. Pertama, dengan modulo $4$, kita dapat mempartisi $A$ menjadi empat subset $L_0, L_1, L_2$ dan $L_3$, di mana $$L_i = {n ∈ A : \text{ }\text{ }\text{ }n ≡ i \text{ }\text{ }\text{ }(\text{mod } 4)}, \text{untuk } i = 0, 1, 2, 3.$$ Lalu ada $500$ angka di masing-masing $L_1, L_2, L_3$ tetapi $499$ angka di $L_0$.
Untuk himpunan $L_1$, susunlah semua angka dalam urutan menaik, dan perhatikan $250$ pasangan yang dibentuk oleh angka-angkanya $(1, 5), (9, 13), (17, 21), . . . , (1993, 1997)$.
Berdasarkan Prinsip Pigeonhole, jika lebih dari $250$ angka di $L_1$ dipilih sebagai bagian dari $L$, maka pasti ada dua angka yang berasal dari salah satu pasangan di atas, sehingga selisihnya adalah $4$. Dengan demikian, angka lebih dari $250$ di $L_1$ tidak dapat dimasukkan ke dalam $L$. Namun, semua angka di tempat ganjil atau semua angka di tempat genap dapat dipilih. Dengan demikian, maksimal $250$ angka dapat dipilih dari $L_1$ sebagai subset dari $L$, dan analisis yang sama berlaku untuk masing-masing $L_2, L_2$, dan $L_0$ (di $L_0$, semua $250$ angka yang merupakan kelipatan ganjil $4$ dapat dipilih untuk dimasukkan ke dalam $L$). Oleh karena itu, jumlah maksimum elemen dalam $L$ adalah $1000$.
Untuk menerapkan prinsip pigeonhole, pasangan yang terdaftar berperan sebagai pigeonhole, dan angka yang dipilih adalah merpati.
Relasi kongruensi adalah metode yang umum digunakan untuk mengklasifikasikan bilangan bulat.
Metode ini juga sering digunakan untuk menerapkan prinsip pigeonhole, seperti yang ditunjukkan pada contoh berikut. - Diberikan $2n − 1$ bilangan bulat positif, buktikan bahwa ada $n$ bilangan bulat positif yang jumlahnya habis dibagi $n$ untuk (1) $n = 3$; (2) $n = 9$.
Solusi: (1) Ketika $n = 3$ maka $2n − 1 = 5$. Bagilah kelima bilangan tersebut berdasarkan sisa pembagian modulo $3$ menjadi tiga kelas: $C_0, C_1$, dan $C_2$.
(i) Jika salah satu dari ketiga kelas tidak berisi bilangan, yaitu lima bilangan berada dalam dua kelas, berdasarkan prinsip pigeonhole, harus ada satu kelas yang berisi setidaknya $3$ bilangan, maka tiga bilangan apa pun yang berasal dari kelas yang sama harus memiliki jumlah yang habis dibagi $3$;
(ii) Jika setiap kelas berisi setidaknya satu bilangan, maka tidak ada kelas yang berisi tiga atau lebih bilangan. Namun, jika dari setiap kelas diambil sebuah bilangan, maka ketiga bilangan tersebut harus memiliki jumlah yang habis dibagi $3$.
(2) Untuk $n = 9$, maka $2n−1 = 17$ bilangan diberikan. Hasil (1) menyiratkan bahwa, dari masing-masing lima bilangan tersebut, tiga bilangan dapat dipilih sedemikian rupa sehingga jumlahnya habis dibagi $3$, sehingga $5$ kelompok $(n_1, n_2, n_3), (n_4, n_5, n_6), · · · , (n_13, n_14, n_15)$ dapat diperoleh secara berurutan dari $17$ bilangan tersebut, sedemikian rupa sehingga jumlahnya $s_1, s_2, · · · , s_5$ semuanya habis dibagi $3$. Misalkan $s_i = 3m_i, i = 1, 2, . . . , 5$ (di mana $m_i$ semuanya bilangan bulat positif). Kemudian, masih dari hasil (1), tiga bilangan, katakanlah $m_1, m_2, m_3$ dapat dipilih dari kelima $m_i$ sedemikian rupa sehingga $m_1 + m_2 + m_3 = 3k$ untuk suatu bilangan bulat positif $k$. Dengan demikian, $$n_1 + n_2 + · · · + n_9 = s_1 + s_2 + s_3 = 3(m_1 + m_2 + m_3) = 9k,$$ yang habis dibagi $9$. - Buktikan bahwa untuk setiap $50$ bilangan bulat positif yang diberikan, selalu mungkin untuk memilih empat bilangan $a_1, a_2, a_3$, dan $a_4$ dari bilangan-bilangan tersebut, sehingga $(a_2 −a_1)(a_4 −a_3)$ merupakan kelipatan $2009$.
Solusi: Pertama-tama, perhatikan bahwa $2009 = 49 × 41$. Perhatikan $50$ sisa dari $50$ bilangan bulat yang diberikan modulo $49$. Berdasarkan prinsip pigeonhole, pasti ada dua bilangan yang dipilih dari $50$ bilangan bulat tersebut, dilambangkan dengan $a_1$ dan $a_2$, sehingga $a_1$ dan $a_2$ kongruen modulo $49$, sehingga $a_2 − a_1$ habis dibagi $49$.
Selanjutnya, dengan alasan yang sama, harus dimungkinkan bahwa dua angka $a_3$ dan $a_4$ dapat dipilih dari $48$ angka yang tersisa sedemikian rupa sehingga $a_4 − a_3$ habis dibagi $41$.
Jadi, $49 · 41 | (a_2 − a_1)(a_4 − a_3)$, yaitu $2009 | (a_2 − a_1)(a_4 − a_3)$. - Buktikan bahwa dalam suatu himpunan yang memuat $n$ bilangan bulat positif pasti ada himpunan bagian yang jumlah semua bilangan di dalamnya habis dibagi $n$.
Solusi: Misalkan $n$ bilangan bulat positif adalah $a_1, a_2, . . . , a_n$. Pertimbangkan $n$ bilangan bulat positif baru: $$b1_ = a_1, b_2 = a_1 + a_2, · · · , b_n = a_1 + a_2 + · · · + a_n.$$ Maka semua nilai $n$ berbeda. Ketika beberapa dari $b_1, b_2, . . . , b_n$ habis dibagi $n$, simpulannya terbukti. Sebaliknya, jika semua $b_i$ tidak habis dibagi $n$, maka sisa-sisanya tidak semuanya nol, yaitu paling banyak mereka dapat mengambil $n − 1$ nilai yang berbeda. Berdasarkan prinsip pigeonhole, harus ada $b_i$ dan $b_j$ dengan $i < j$ sehingga $b_j − b_i \neq 0$ habis dibagi $n$. Karena $b_j − b_i = a_i + 1 + a_i + 2 + · · · + a_j$ adalah jumlah dari beberapa bilangan yang diberikan, kesimpulannya terbukti. - Jika lima titik diambil secara acak dari dalam sebuah persegi dengan sisi $1$, buktikan bahwa pasti ada dua titik sedemikian rupa sehingga jarak antara kedua titik tersebut tidak lebih besar dari $\frac{\sqrt{2}}{2}$.
Solusi: Dengan menghubungkan dua titik tengah dari dua sisi yang berhadapan, persegi tersebut dibagi menjadi empat persegi kongruen yang lebih kecil dengan sisi $\frac{1}{2}$. Berdasarkan prinsip lubang merpati, harus ada satu persegi yang memuat setidaknya $2$ titik.
Karena persegi kecil tersebut ditutupi oleh lingkaran dengan pusat yang sama dan jari-jari $\sqrt{2}/4$, maka jarak antara dua titik di dalam lingkaran tidak lebih besar dari diameternya, yaitu $\sqrt{2}/2$ Kesimpulannya terbukti. - Terdapat enam titik di dalam ruang sedemikian rupa sehingga setiap tiganya tidak kolinear. Jika dua titik dihubungkan oleh sebuah ruas garis, dan setiap ruas garis diwarnai dengan salah satu warna merah atau biru, buktikan bahwa setidaknya harus ada satu segitiga yang dibentuk oleh tiga titik dan ruas garis yang menghubungkannya, sedemikian rupa sehingga ketiga sisinya berwarna sama.
Solusi: Misalkan keenam titik tersebut adalah $A_0, A_1, A_2,A_3, A_4$, dan $A_5$. Perhatikan segmen-segmen yang menghubungkan titik-titik ini. Kita menggunakan segmen riil untuk menunjukkan segmen merah dan segmen titik untuk menunjukkan segmen biru, seperti yang ditunjukkan pada diagram.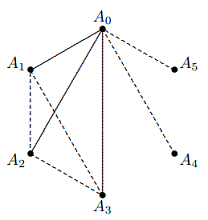
Perhatikan lima segmen yang dimulai dari $A_0:
A_0A_1, A_0A_2, A_0A_3, A_0A_4, A_0A_5$. Masing-masing diwarnai dengan warna merah atau biru. Berdasarkan Prinsip Pigeonhole, di antara kelima segmen tersebut harus terdapat setidaknya tiga segmen dengan warna yang sama. Tanpa mengabaikan keumuman, dapat diasumsikan bahwa tiga segmen berwarna merah, yaitu $A_0A_1, A_0A_2, A_0A_3$.
Sekarang perhatikan tiga sisi segitiga $A_1A_2A_3$. Jika salah satu sisinya berwarna merah, maka terdapat segitiga merah, artinya ketiga sisinya semuanya berwarna merah. Jika tidak, jika ketiga sisi $\Delta A_1A_2A_3$ semuanya berwarna biru, maka kesimpulannya juga benar.
“It is better to fail in originality than to succeed in imitation.”
