Pembagian Polinomial

- Pembagian Panjang
- Divisi Sintetis
- Teorema Sisa dan Teorema Faktor
- Faktorisasi Polinomial Simetris atau Siklik
- Contoh Soal
Pembagian Panjang
Pembagian Panjang: Ketika bilangan bulat $n$ dibagi dengan bilangan bulat bukan nol $m$, hasil bagi $q$ dan sisa $r$ dapat diperoleh. Hasilnya dapat ditulis dalam bentuk $n = mq + r$, di mana $0 ≤ r < m$, dan proses untuk mendapatkan ekspresi tersebut disebut pembagian dengan sisa.
Dalam pembagian polinomial, ketika polinomial $f(x)$ dibagi dengan polinomial bukan nol $g(x)$ dengan pembagian biasa (pembagian panjang), terdapat hasil bagi $q(x)$ dan sisa $r(x)$, di mana derajat $f$ adalah jumlah dari derajat $g$ dan $q$, dan derajat $r$ lebih kecil dari derajat $g$. Hasilnya dapat ditulis dalam bentuk $$f(x) = g(x) · q(x) + r(x).$$
Divisi Sintetis
Divisi Sintetis. Jika pembagi $g(x) = x − a$, dengan $a$ adalah konstanta, maka $q(x)$ adalah polinomial berderajat $n − 1$ jika derajat $f(x)$ adalah $n$, dan sisa $r$ adalah konstanta. Tuliskan $$f(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0,$$ $$q(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-1}+…+b_1x+b_0.$$ Karena $$f(x)=(x-a)(b_{n-1}x^{n-1}+b_{n-2}x^{n-1}+…+b_1x+b_0)+r$$ $$=b_{n-1}x^n+(b_{n-2}-ab_{n-1})x^{n-1}+(b_{n-3}-ab_{n-2})x^{n-2}+…+(b_0-ab_1)x-ab_0+r,$$ dengan membandingkan koefisien $f(x)$, kita memperoleh $$b_{n-1}=a_n,b_{n-1}=a_{n-1}+ab_{n-1},…,b_0=a_1+ab_1,r=a_0+ab_0.$$ Dengan demikian diperoleh tabel operasi sebagai berikut: 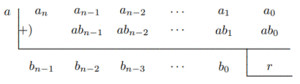
Teorema Sisa dan Teorema Faktor
Teorema I. Teorema Sisa: Untuk setiap konstanta $a$, polinomial $f(x)$ berderajat $n ≥ 1$ dapat ditulis dalam bentuk $f(x) = (x − a)q(x) + r$, $q(x)$ adalah polinomial berderajat $n − 1$, dan $r = f(a)$.
Untuk setiap konstanta $a$ dan $b$ yang diberikan, polinomial $f(x)$ berderajat $n ≥ 2$ dapat ditulis dalam bentuk $f(x) = (x − a)(x − b)q(x) + r(x)$, dengan $q(x)$ adalah polinomial berderajat $n − 2$, dan sisa $r(x)$ adalah polinomial nol atau berderajat 1 atau nol.
Teorema II. Teorema Faktor: Suatu polinomial $f(x)$ mempunyai faktor $(x − a)$ jika dan hanya jika $f(a) = 0$.
Teorema III. Untuk polinomial dengan koefisien integral $f(x) =a_nx^n +a_{n-1}x^{n−1} + · · · + a_1x + a_0$, jika memiliki faktor $x −\frac{q}{p}$, di mana $p, q$ adalah dua bilangan bulat yang relatif prima, maka $q$ adalah faktor dari $a_0$, dan $p$ adalah faktor dari $a_n$.
Bukti. Dengan teorema faktor, $f\left(\frac{q}{p}\right)=0$, oleh karena itu $$0=a_n\left(\frac{q}{p}\right)^n+a_{n-1}\left(\frac{q}{p}\right)^{n-1}+…+a_1\left(\frac{q}{p}\right)+a_0$$ $$o=a_nq^n+a_{n-1}pq^{n-1}+…+a_1p^{n-1}q+a_0p^n,$$ $$-a_0p^n=(a_nq^{n-1}+a_{n-1}pq^{n-2}+…+a_1p^{n-1})q,$$
jadi $q|a_0p^n$, yang menyiratkan bahwa $q|a_0$ maka $(p,q)=1$. Demikian pula, kita memiliki $$-a_nq^n=(a_{n-1}q^{n-1}+a_{n-1}pq^{n-2}+…+a_1p^{n-2}+…+a_1p^{n-2}q+a)p^{n-1})p,$$ jadi $p|a_nq^n$, yang menyiratkan bahwa $p|a_n$ maka $(p,q)=1$.
Faktorisasi Polinomial Simetris atau Siklik
Faktorisasi Polinomial Simetris atau Siklik. Suatu polinomial dengan banyak variabel disebut simetris jika polinomial tersebut tidak berubah oleh permutasi variabel apa pun. Misalnya, $x + y + z, x^2 + y^2 + z^2, xy^2$, dst.
Suatu ekspresi simetris yang memuat dua variabel $x$ dan $y$ selalu dapat difaktorkan sebagai hasil perkalian faktor-faktor yang dinyatakan dalam bentuk ekspresi simetris dasar $(x+y), xy$; suatu ekspresi simetris yang memuat tiga variabel $x, y, z$ selalu dapat difaktorkan sebagai hasil perkalian faktor-faktor yang dinyatakan dalam bentuk ekspresi simetris dasar $(x + y + z), xy + yz + zx, xyz.$
Suatu polinomial multivariabel disebut siklik jika setelah semua variabelnya diubah secara siklik, polinomial yang dihasilkan tidak berubah. Misalnya, $xy+yz+zx, x^2y+y^2z+z^2x,(x+y)(y+z)(z+x)$, dst. Polinomial simetris harus siklik, tetapi kebalikannya tidak berlaku.
Jika suatu polinomial siklik memiliki faktor, maka ekspresi yang diperoleh dengan mengubah variabel-variabel faktornya secara siklik merupakan semua faktor dari polinomial tersebut, karena faktorisasi polinomial tersebut juga bersifat siklik. Berdasarkan fitur ini, kita dapat menganggap salah satu variabel sebagai variabel utama, dan variabel lainnya sebagai konstanta pada saat itu, sehingga kita mendapatkan polinomial dengan satu variabel. Maka, mudah untuk menemukan faktor dengan menggunakan teorema faktor, dan dengan menggunakan fitur siklik faktor-faktor di atas, kita dapat memperoleh faktor-faktor lainnya sekaligus. Terakhir, jika terdapat beberapa koefisien konstan yang perlu ditentukan, maka metode penentuan koefisien (BAB 6) berguna untuk hal ini.
Contoh Soal
- (i) Jika $f(x) = 3x^2 + 5x − 7$ dibagi dengan $x + 2$, carilah hasil bagi dan sisanya dengan pembagian panjang.
(ii) Jika $f(x) = 3x^4 −5x^3 +x^2 + 2$ dibagi dengan $x^2 + 3$, carilah hasil bagi dan sisanya dengan pembagian bersusun.Solusi: Dengan pembagian panjang berikut:
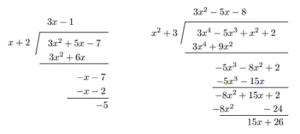
Oleh karena itu
(i) $q(x)=3x-1,\text{ }r=-5.$ (ii) $q(x)=3x^2-5x-8,\text{ }r(x)=15x+26$
Catatan: Silakan bandingkan pembagian panjang untuk bilangan bulat dan pembagian untuk polinomial, apa saja persamaannya dan apa saja perbedaannya? - Gunakan pembagian sintetis untuk mencari hasil bagi dan sisa dari polinomial $2x^4 − 3x^3 − x^2 + 5x + 6$ jika dibagi dengan $x + 1$.
Solusi: Dengan menggunakan pembagian sintetis, diperoleh hasil sebagai berikut:
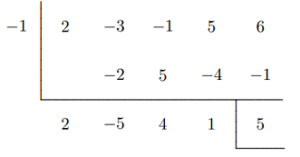
Maka, $q(x)=2x^3-5x^2+4x+1$, $r=5$.
Ketika polinomial $f(x)$ dibagi dengan $g(x) = ax+b$, di mana $a \neq 1$ dan $a \neq 0$, pembagian sintetis masih berfungsi, karena $$f(x)=(ax+b)q(x)+r=\left(x+\frac{b}{a}\right)\cdot (aq(x)).$$ Jadi, kita misalkan pembaginya adalah $x+\frac{b}{a}$ untuk menggunakan pembagian sintetis terlebih dahulu, setelah mendapatkan $ag(x)$ dan $r$, $q(x)$ dan $r$ diperoleh sekaligus. - Tentukan hasil bagi dan sisa hasil bagi polinomial $6x^4−7x^3−x^2+8$ jika dibagi $2x + 1$.
Solusi: Dengan menggunakan pembagian sintetis untuk melakukan pembagian $(6x^4-7x^3-x^2+8)\div (x+\frac{1}{2})$:
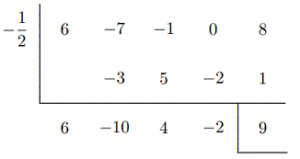
oleh karena itu $2q(x)=6x^3-10x^2+4x-2$, $r=9$, maka $q(x)=3x^3-5x^2+2x-1$, $r=9$. Perhatikan bahwa sisa $r$ tidak terpengaruh oleh perubahan pembagi. - Jika suatu polinomial $f(x)$ mempunyai sisa $3$ dan $5$ ketika dibagi dengan $x − 1$ dan $x−2$, carilah sisa ketika $f(x)$ dibagi dengan $(x−1)(x−2)$.
Solusi: Dari Teorema Sisa, $$f(x)=(x-1)q_1(x)+3\text{ dan }q_1(x)=(x-2)q_2(x)+r,$$ di mana $q_1(x)$ adalah hasil bagi $f$ jika dibagi $x − 1, q_2, r$ masing-masing adalah hasil bagi dan sisa $q_1$ jika dibagi $x − 2$. Maka $$f(x) = (x − 1)[(x − 2)q_2(x) + r] + 3 = (x − 1)(x − 2)q_2(x) + r(x − 1) + 3.$$ Berdasarkan Teorema Sisa, kita peroleh $5 = f(2) = r(2−1) + 3 = r + 3$, sehingga $r = 2.$
Jadi, sisa $f$ jika dibagi dengan $(x − 1)(x − 2)$ adalah $2x + 1.$ - Jika suatu polinomial $f(x)$ habis dibagi oleh $x − a$ dan $x − b$, di mana $a, b$ merupakan dua konstanta yang berbeda, buktikan bahwa $f(x)$ pasti habis dibagi oleh $(x − a)(x − b)$.
Solusi: Mirip dengan pertanyaan sebelumnya, mari kita $$f(x) = (x − a)q_1(x) \text{ dan } q_1(x) = (x − b)q_2(x) + r,$$ maka $$f(x) = (x − a)[(x − b)q_2(x) + r] = (x − a)(x − b)q_2(x) + r(x − a).$$ Dengan Teorema Faktor, $$0 = f(b) = r(b − a), ∴ r = 0.$$ Dengan demikian, $f(x) = (x − a)(x − b)q_2(x)$, kesimpulannya terbukti.
- Faktorkan $f(x)=x^4+x^3-7x^2-x+6$.
Solusi: Dari Teorema IV, jika $f(x) = 0$ memiliki akar-akar rasional, maka akar-akar tersebut pastilah akar integral, dan berada dalam himpunan $S = {±1, ±2, ±3, ±6}$. Karena $f(1) = f(−1) =0$, berdasarkan teorema faktor, $f$ memiliki faktor $(x − 1)$ dan $(x + 1)$. Untuk memeriksa bilangan-bilangan lain dalam $S$, dengan pembagian sintetis,
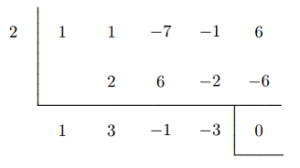
Oleh karena itu, hasil bagi $q_1(x)$ dari $f(x)$ jika dibagi dengan $(x−2)$ adalah $x^3 + 3x^2 −x−3$, sisanya $0$, sehingga $x−2$ adalah faktor ketiga dari $f(x)$. Selanjutnya, kita periksa faktor $x+3$.
Dengan divisi sintetis,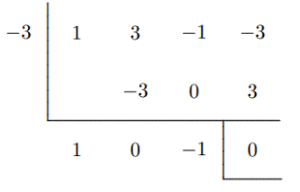
Dengan demikian, hasil bagi $q_2(x)$ dari $x^3 + 3x^2 −x−3$ jika dibagi dengan $x+3$ adalah $x^2 −1$, dan sisanya adalah $0$. Jadi, $x + 3$ adalah faktor keempat. Dengan demikian, $$f(x) = (x − 1)(x + 1)(x − 2)(x + 3).$$ - Faktorkan ekspresi simetris $(x+y+z)^5-x^5-y^5-z^5$.
Solusi: Dengan mengambil $x$ sebagai variabel utama, kita mendefinisikan $f(x) = (x + y +z)^5 − x^5 − y^5 − z^5$. Karena $$f(−y) = z^5 − (−y)^5 − y^5 − z^5 = 0,$$ $(x+y)$ merupakan faktor dari ekspresi asli, dan begitu pula ekspresi $(y + z)$ dan $(z + x)$. Asumsikan bahwa $$(x+y+z)^5−x^5−y^5−z^5 = (x+y)(y+z)(z+x)[A(x^2+y^2+z^2)+B(xy+yz+zx)],$$ maka perbandingan koefisien $x^4y$ pada kedua ruas menghasilkan $A = 5$. Misalkan $x = y = z = 1$, maka $243 − 3 = 8[15 + 3B]$, sehingga $B = 5$. Jadi, $$(x+y+z)^5−x^5−y^5−z^5 = 5(x+y)(y+z)(z+x)(x^2+y^2+z^2+xy+yz+zx).$$
- Faktorkan $(b-c)^3+(c-a)^3+(a-b)^3$.
Solusi: Dengan mengambil $a$ sebagai variabel utama dan misalkan $f(a) = (b− c)^3 + (c −a)^3 + (a − b)^3$, maka $$f(b) = (b − c)^3 + (c − b)^3 = 0,$$ Jadi $(a− b)$ adalah faktor dari persamaan aslinya. Oleh karena itu, $(b− c)$ dan $(c−a)$ juga merupakan faktornya. Jadi, $$(b − c)^3 + (c − a)^3 + (a − b)^3 = A(b − c)(c − a)(a − b),$$ di mana $A$ adalah konstanta yang akan ditentukan. Misalkan $a = 2, b = 1, c = 0$ pada kedua sisi, maka $−6 = −2A$, sehingga $A = 3$. Jadi, $$(b − c)^3 + (c − a)^3 + (a − b)^3 = 3(b − c)(c − a)(a − c).$$
Catatan: Dengan mempertimbangkan $(b − c) + (c − a) + (a − b) = 0$, hasil di atas dapat diperoleh dengan menggunakan rumus $u^3 + v^3 + w^3 − 3uvw = (u + v + w)(u^2 + v^2 +w^2 − uv − vw − wu)$ sekaligus. - Faktorkan $a^3(b-c)+b^3(c-a)+c^3(a-b)$.
Solusi: Mengambil $a$ sebagai variabel utama dan $f(a) = a^3(b − c) + b^3(c −a) + c^3(a − b)$, kita memperoleh $$f(b) = b^3(b − c) + b^3(c − b) = 0,$$ jadi $(a-b),(b-c),(c-a)$ semuanya adalah faktor dari ekspresi asli. Maka $$a^3(b − c) + b^3(c − a) + c^3(a − b) = A(a + b + c)(a − b)(b − c)(c − a).$$ Misalkan $a=2,b=1,c=0$, maka $8-2=-6A$, yaitu $A=-1$. Maka $$a^3(b − c) + b^3(c − a) + c^3(a − b) = (a + b + c)(b − c)(a − c)(a − b).$$
Solusi dari setiap Permasalahan diberikan pada kelas online
“Do not stop thinking of life as an adventure. You have no security unless you can live bravely, excitingly, imaginatively; unless you can choose a challenge instead of competence.”

