Luas Segitiga dan Aplikasi Luas

Pengantar Pemecahan Masalah

Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit

Kelas

Materi ini ditunjukan untuk siswa berbakat kelas 4, 5, 6, 7 dan 8

Presentasi

Unduh

Video Pengantar

fira

Video Lanjutan

Pre Test

Post Test

Referensi Tambahan

Unduh

Rumus dasar luas segitiga

Catatan: Luas segitiga $UVW$ dilambangkan dengan $[UVW]$ selanjutnya.

Teorema I. Untuk $\Delta ABC,[ABC]=\frac{1}{2}a\cdot h_a=\frac{1}{2}b\cdot h_b=\frac{1}{2}c\cdot h_c$ dimana $BC=a,CA=b,AB=c$ dan $h_a,h_b,h_c$ adalah ketinggian pada $BC,CA,AB$ masing-masing.

Teorema II. (Rumus Heron) Untuk $\Delta ABC,[ABC]=\sqrt{s(s-a)(s-b)(s-c)}$, dimana $s=\frac{1}{2}(a+b+c)$.

Bukti: Untuk $\Delta ABC$, misalkan $BC=a,CA=b,AB=c$ dan $AD=h$, dimana $AD\bot BC$ di $D$. Misalkan $CD=x$, maka $$c^2-(a-x)^2=h^2=b^2-x^2,$$ $$c^2-a^2+2ax=b^2,$$ $$∴x=\frac{a^2+b^2-c^2}{2a}.$$ Oleh karena itu, $$h^2=b^2-\left(\frac{a^2+b^2-c^2}{2a}\right)^2=\frac{1}{4a^2}[(2ab)^2-(a^2+b^2-c^2)^2]$$ $$=\frac{(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)}{4a^2}$$ $$=\frac{[(a+B)^2-c^2][c^2-(a-b)^2]}{4a^2}$$ $$=\frac{(a+b+c)(a+b-c)(c+a-b)(c-a+b)}{4a^2}$$ $$=\frac{16}{4a^2}p(p-c)(p-b)(p-a)=\frac{4p(p-a)(p-b)(p-c)}{a^2}.$$ $$∴[ABC]^2=\left(\frac{h_a}{2}\right)^2=p(p-a)(p-b)(p-c).$$ Dengan demikian, kesimpulannya terbukti.
Catatan: Jika $∠C$ tumpul, maka $c^2 > a^2 + b^2$, sehingga $x < 0$, tetapi pembuktiannya tetap tidak berubah.

Perbandingan luas segitiga

(I) Untuk setiap segitiga, misalkan $S = h \cdot b$, di mana $b$ adalah salah satu sisi dan $h$ adalah tinggi sisi tersebut. Maka, rasio luas dua segitiga mana pun sama dengan rasio dua $S$ yang bersesuaian.
(II) Untuk dua segitiga dengan alas yang sama, rasio luasnya sama dengan rasio tingginya pada alas tersebut. Oleh karena itu, luas segitiga tidak berubah ketika titik sudutnya bergerak pada garis yang sejajar dengan sisi di depannya.
(III) Untuk dua segitiga dengan tinggi yang sama, rasio luasnya sama dengan rasio alasnya.
(IV) Jika dua segitiga memiliki sepasang sudut yang sama besar, maka rasio luasnya sama dengan rasio hasil perkalian kedua sisi sudut yang sama besar tersebut.
(V) Jika dua segitiga mempunyai sepasang sudut bersuplemen, maka rasio luasnya sama dengan rasio hasil perkalian kedua sisi sudut bersuplemen tersebut.

Ada dua jenis pertanyaan yang akan dibahas dalam bab ini. Pertama, pertanyaan untuk menemukan area atau membahas pertanyaan yang melibatkan area. Kedua, pertanyaan yang dapat dipecahkan dengan mempertimbangkan area. Berikut ini beberapa contoh dari kedua jenis pertanyaan tersebut.

Contoh Soal

Misalkan luas $\Delta ABC = 10 \text{ cm}^2, AD = 2 \text{ cm}, DB = 3 \text{ cm}$ dan luas $\Delta ABE$ sama dengan luas segi empat $DBEF$. Maka luas $\Delta ABE$ sama dengan
(A) $4\text{ cm}^2$ (B) $5\text{ cm}^2$ (C) $6\text{ cm}^2$ (D) $7\text{ cm}^2$ (E) $8\text{ cm}^2$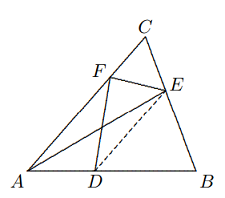

Solusi: Hubungkan $DE$. Karena $[ABE] = [DBEF]$, kita memiliki $$[ADE] = [ABE] − [DBE]$$ $$= [DBEF] − [DBE] = [FDE],$$ $$∴ AC || DE,$$ $$∴ CE : EB = AD : DB = 2 : 3.$$ $$∵\frac{[ABE]}{[ABC]}=\frac{BE}{BC}=\frac{3}{5},$$ $$∴ [ABE] =\frac{3}{5}\cdot [ABC]=6.$$ Jawabannya adalah (B).
Pada diagram yang diberikan, $ABCD$ adalah segi empat cembung. Carilah titik $M$ pada ruas $BC$ sehingga $AM$ membagi $ABCD$ menjadi dua bagian dengan luas yang sama.

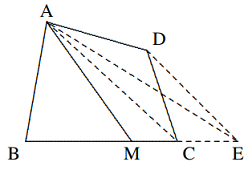
Solusi: Kita perlu mengubah bentuk grafik dari segi empat menjadi segitiga, dengan luas yang tetap sama. Dari $D$, masukkan $ED || AC$ sehingga $DE$ berpotongan dengan perpanjangan garis $BC$ di $E$. Maka $$[DAC]=[EAC],∴ [ABCD] = [EAB].$$ Sekarang mengambil $M$ menjadi titik tengah $BE$, maka $$ABM] = [AEM] = \frac{1}{2}[ABCD]$$ $$= [AMCD].$$
Pada $\Delta ABC, D, E$ masing-masing berada pada $BC$ dan $CA$, dan $BD : DC = 3 : 2, AE : EC = 3 : 4$. $AD$ dan $BE$ berpotongan di $M$. Diketahui luas $\Delta ABC$ adalah $1$, tentukan luas $\Delta BMD$.

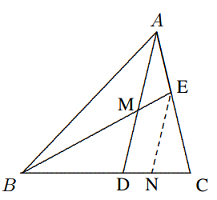
Solusi: Dari $E$ masukkan $EN || AD$, berpotongan dengan $BC$ di $N$. Karena $$\frac{DN}{NC}=\frac{AE}{EC}=\frac{3}{4},\frac{BC}{DC}=\frac{3}{2},$$ $$[ABE]=\frac{3}{7}[ABC]=\frac{3}{7},$$ $$∴[BEC]=\frac{4}{7}[ABC]=\frac{4}{7}.$$ $$∵ BD : DN : NC = 21 : 6 : 8,$$ $$∴ BN : NC = 27 : 8\text{ dan}$$ $$BD : BN = 21 : 27 = 7 : 9, [BEN] = \frac{27}{35}[BEC]=\frac{27}{35}\cdot \frac{4}{7},$$ $$[BMD]=\left(\frac{7}{9}\right)^2[BEN]=\frac{7^2\cdot 27\cdot 4}{9^2\cdot 35\cdot 7}=\frac{4}{15}.$$
Segi lima cembung ABCDE memiliki sifat sebagai berikut: kelima segitiga $ABC, BCD, CDE, DEA, EAB$ memiliki luas yang sama $1$. Buktikan bahwa semua segi lima tersebut memiliki luas yang sama, dan terdapat tak terhingga banyaknya segi lima yang berbeda.

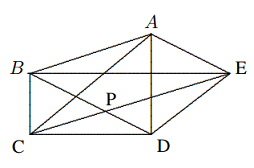
Solusi: Seperti yang ditunjukkan pada diagram di sebelah kanan, persamaan $[EAB] = [CAB]$ menghasilkan $EC || AB$. Demikian pula, kita memiliki $$AD || BC, BE || CD, AC || DE, BD || AE.$$ Misalkan $[BPC] = x$. Maka $[DPC] = 1 − x$ dan $$\frac{[BPC]}{[DPC]}=\frac{BP}{PD}=\frac{[EBP]}{[EPD]},$$ maka diperoleh $\frac{x}{1-x}=\frac{1}{x},$ $$∴ x^2 + x − 1 = 0, x=\frac{\sqrt{5}-1}{2},$$ $$∴ [ABCDE] = 3 + x = \frac{5+\sqrt{5}}{2}.$$
Pada segi empat $ABCD$, titik $E, F$ berada pada $AB$ dan $H, G$ berada pada $DC$ sehingga $AE = EF = FB$ dan $DH = HG = GC$. Buktikan bahwa $[EFGH] = \frac{1}{3}[ABCD]$.

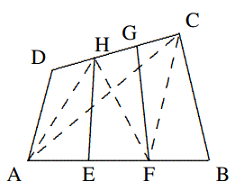
Solusi: Hubungkan $HF, AH, AC, FC$. $$∵ [HEF] = [HEA]\text{ dan } [FGH] = [FGC],$$ $$∴ [EFGH] = \frac{1}{2}[HAFC].$$ Cukup untuk menunjukkan bahwa $[ADH] + [CFB] =\frac{1}{3}[ABCD]$.
Dari $DH=\frac{1}{3}CD$ dan $FB=\frac{1}{3}AB$, kita memiliki $$[ADH]+[CFB]=\frac{1}{3}([DAC]+[BAC])=\frac{1}{3}[ABCD],$$ $$∴[EFGH]=\frac{1}{2}[HAFC]=\frac{1}{2}\cdot \frac{2}{3}[ABCD]=\frac{1}{3}[ABCD].$$
Seperti yang ditunjukkan pada gambar, segitiga $ABC$ dibagi menjadi enam segitiga yang lebih kecil oleh garis yang ditarik dari titik sudutnya melalui sebuah titik interior yang sama. Luas keempat segitiga ini adalah seperti yang ditunjukkan. Temukan luas segitiga $ABC$.

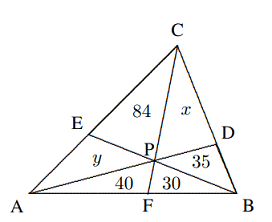
Solusi: $\frac{[CAP]}{[FAP]}=\frac{CP}{FP}=\frac{[CBP]}{[FBP]}$ menghasilkan $$\frac{84+y}{40}=\frac{x+35}{30},\text{ }\text{ }\text{ }(14.1)$$ dan $\frac{[CAP]}{[CDP]}=\frac{AP}{DP}=\frac{[BAP]}{[BDP]}$ menghasilkan $$\frac{84+y}{x}=\frac{70}{35}=2.\text{ }\text{ }\text{ }(14.2)$$ Dengan $\frac{(2)}{(1)}$, diperoleh bahwa $\frac{x}{40}=\frac{x+35}{60}$,
$∴ 3x = 2x + 70$, yaitu $x=70$. Maka dengan $(2)$, $y=140-84=56$.
Maka, $[ABC]=84+56+40+30+35+70=315$.
Jika dari sembarang titik dalam tetap $P$ pada $\Delta ABC$, masukkan $PD ⊥ BC$ di
$D$ $PE ⊥ CA$ di $E$, dan $PF ⊥ AB$ di $F$. Buktikan bahwa $\frac{PD}{h_a}+\frac{PE}{h_b}+\frac{PF}{h_c}= 1$, di mana $h_a, h_b, h_c$ adalah tinggi $\Delta ABC$ yang dimasukkan dari $A, B, C$ ke sisi-sisi yang berhadapan.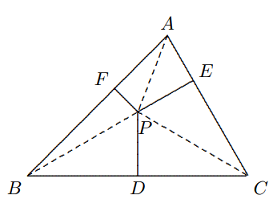

Solusi: Dari $$\frac{PD}{h_a}=\frac{[PBC]}{[ABC]},$$ $$\frac{PE}{h_b}=\frac{[PCA]}{[ABC]},$$ $$\frac{PF}{h_c}=\frac{[PAB]}{[ABC]},$$ diperoleh bahwa $$\frac{PD}{h_a}+\frac{PE}{h_b}+\frac{PF}{h_c}=\frac{[PBC]+[PCA]+[PAB]}{[ABC]}=1.$$
Pada $\Delta ABC$, $M$ adalah titik tengah $BC, P, R$ masing-masing berada pada $AB, AC, Q$ adalah titik potong $AM$ dan $PR$. Jika $Q$ adalah titik tengah $PR$, buktikan bahwa $PR || BC$.

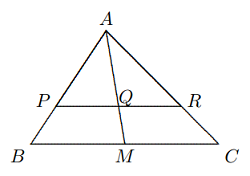
Solusi: Dari $Q$ tersebut, $M$ masing-masing adalah titik tengah $PR$ dan $BC$, $$[APQ] = [ARQ], [ABM] = [ACM],$$ $$∴\frac{[APQ]}{[ABM]}=\frac{[ARQ]}{[ACM]},$$ $$∴\frac{AP\cdot AQ}{AB\cdot AM}=\frac{AQ\cdot AR}{AM\cdot AC},$$ $$\text{yaitu, }\frac{AP}{AB}=\frac{AR}{AC},\text{ }∴PQ||BC.$$
Pada diagram di bawah ini, $ABCD$ adalah jajargenjang, $E, F$ adalah dua titik pada sisi $AD$ dan $DC$, sehingga $AF = CE$. $AF$ dan $CE$ berpotongan di titik $P$. Buktikan bahwa $PB$ membagi dua $∠APC$.

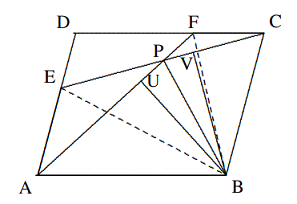
Solusi: Hubungkan $BE, BF$, buat $BU ⊥ AF$ di $U$ dan $BV ⊥ CE$ di $V$. Maka $$[BAF]=[BCE]=\frac{1}{2}[ABCD].$$ Selanjutnya, karena $AF = CE$, kita memiliki $$BU = BV, ∴ \Delta BPU \cong \Delta BPV,$$ $$∴ ∠BPA = ∠BPU = ∠BPV = ∠BPC.$$