Aplikasi Teorema Titik Tengah

- Contoh Soal
Pada segitiga, ruas garis yang menghubungkan titik tengah dua sisi disebut garis tengah segitiga. Segitiga memiliki tiga garis tengah.
Pada trapesium, ruas garis yang menghubungkan titik tengah dua kaki disebut garis tengah trapesium.
Teorema I. Untuk setiap segitiga $ABC$, jika $D$ dan $E$ masing-masing berada pada $AB$ dan $AC$, maka $DE || BC$ dan $DE = \frac{1}{2}BC$ jika dan hanya jika $D, E$ masing-masing adalah titik tengah $AB$ dan $AC$.
Teorema II. Untuk trapesium $ABCD$ dengan $AB || CD$, jika $E, F$ masing-masing adalah titik tengah $AD$ dan $BC$, maka $EF || AB || CD$, dan $EF = \frac{1}{2}(AB + CD)$.
Dalam geometri, kedua teorema ini sering digunakan, karena titik ujung garis tengah merupakan titik tengah sisi-sisi, sehingga banyak soal penentuan titik tengah dapat diselesaikan dengan menggunakan garis tengah.
Karena garis tengah adalah setengah dari sisi ketiga untuk segitiga, atau setengah dari jumlah dua alas untuk trapesium, garis tengah dapat digunakan sebagai alat untuk mengubah segmen-segmen yang akan dibandingkan atau diidentifikasi menjadi setengah dari dua kali lipat segmen-segmen tersebut, sehingga perbandingannya menjadi jauh lebih mudah.
Contoh Soal
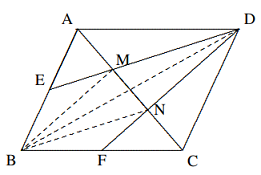
- Pada gambar, $D, E$ adalah titik-titik pada $AB$ dan $AC$ sehingga $AD = DB, AE = 2EC$, dan $BE$ berpotongan dengan $CD$ di titik $F$. Buktikan bahwa $4EF = BE$.
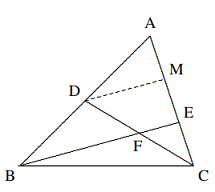
Solusi: Sulit untuk membandingkan panjang $EF$ dan $BE$ karena keduanya berada pada garis yang sama. Di sini, kita dapat menggunakan garis tengah sebagai penggaris untuk mengukurnya.
Misalkan $M$ adalah titik tengah $AE$. Hubungkan $DM$. Dengan menerapkan teorema titik tengah
pada $\Delta ABE$ dan $\Delta CDM$ secara berurutan, maka $$DM=\frac{1}{2}BE,$$ $$EF=\frac{1}{2}DM$$ $$∴EF=\frac{1}{4}BE, \text{ yaitu, }BE=4EF.$$ - Diketahui $ABCD$ merupakan segiempat cembung, $∠ABC = ∠CDA = 90◦$, dan $∠BCD > ∠BAD$, seperti yang ditunjukkan pada diagram di bawah ini. Buktikan bahwa $AC > BD$.
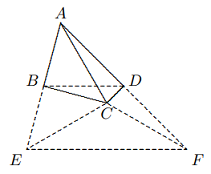
Solusi: Perluas $AB, AD$ ke $E, F$ secara berurutan, sehingga $AB = BE$ dan $AD = DF$. Kemudian, dengan teorema titik tengah, $$BD||EF\text{ dan }EF=2BD.$$ Karena $BC, DC$ masing-masing adalah garis bagi tegak lurus dari $AE, AF$, $$EC=AC=FC.$$ Dari pertidaksamaan segitiga, $$EC+FC>EF,\text{ yaitu }$$ $$2AC > 2BD, ∴ AC > BD.$$ - Seperti yang ditunjukkan pada gambar, pada $\Delta ABC, ∠B = 2∠C$, $AD$ tegak lurus $BC$ di titik $D$ dan $E$ adalah titik tengah $BC$. Buktikan bahwa $AB = 2DE$.
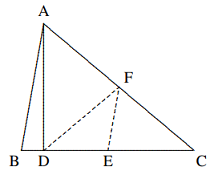
Solusi: Misalkan $F$ adalah titik tengah $AC$, hubungkan $EF, DF$. Dengan teorema titik tengah, $AB = 2EF$, cukup ditunjukkan $DE = EF$. Karena $DF$ adalah median pada hipotenusa $AC$ dari segitiga siku-siku $ADC, DF = F C = AF$, maka $∠CDF = ∠C$. Karena $EF || AB$, $$∠CEF = ∠B = 2∠C,$$ $$∴ ∠DFE = ∠CEF − ∠CDF = ∠C$$ $$= ∠CDF, \text{ maka }DE = EF.$$ - Pada gambar, $AB = CD, E, F$ masing-masing adalah titik tengah $AD$ dan $BC$. Misalkan $BA$ berpotongan dengan $FE$ di $M$. Buktikan bahwa $AM = AE$.
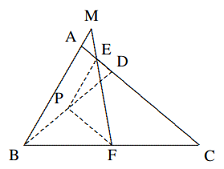
Solusi: Kondisi yang diberikan $AB = CD$ dan tujuan $AM = AE$ tidak memiliki hubungan langsung. Di sini, teorema titik tengah adalah jembatan yang menghubungkan keduanya.
Hubungkan $BD$. Misalkan $P$ adalah titik tengah $BD$, hubungkan $PE, PF$. Maka, dengan teorema titik tengah, $$PE=\frac{1}{2}AB=\frac{1}{2}CD=PF$$ dan $PE||BM,\text{ }AC||PF$. Oleh karena itu, $$∠AME = ∠PEF = ∠PFE = ∠AEM,$$ $$∴ AM = AE.$$ - Untuk segi empat $ABCD, E, F$ masing-masing adalah titik tengah $AB$ dan $BC$, $DE$ dan $DF$ berpotongan dengan diagonal $AC$ di titik $M$ dan $N$, sehingga $AM = MN = NC$. Buktikan bahwa $ABCD$ adalah jajargenjang.
Solusi: Pertama-tama, kita tunjukkan bahwa $MBND$ adalah jajargenjang, lalu kita tunjukkan bahwa $ABCD$ adalah jajargenjang. Pada langkah pertama, teorema titik tengah memainkan peran penting.
$$\text{Hubungkan } BM, BD, BN. ∵ AE = BE,$$ $$BF = F C, \text{ dan } AM = MN = NC,$$ $$EM || BN \text{ dan } FN || BM,$$ $∴ MBND$ adalah jajargenjang. Maka $$BM = ND\text{ dan }∠AMB = ∠FNM = CND,\Delta AMB \cong \Delta CND \text{ (S.A.S.)},$$ $$∴ AB = CD, ∠BAC = ∠DCN,$$ Jadi, $AB || CD$ juga. Maka, $ABCD$ adalah jajargenjang. - Pada trapesium $ABCD, AD || BC, ∠B =30◦,∠C = 60◦, E, M, F, N$ berturut-turut adalah titik tengah $AB, BC, CD, DA$. Diketahui $BC = 7, MN = 3$. Tentukan $EF$.
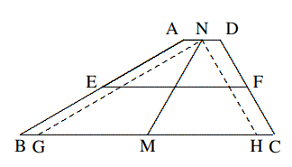
Solusi: Dengan menerapkan teorema titik tengah pada trapesium, maka $EF = \frac{1}{2} (AD + BC)$, sehingga penting untuk mencari $AD$.
Melalui $N$, kita masukkan $NG || AB, NH || CD$, yang berpotongan dengan $BC$ di $G$, $H$ masing-masing. Karena $AD || BC$, segiempat $ABGN$ dan $NHCD$ keduanya merupakan jajar genjang. $$∴ BG = AN = CH = ND \text{ dan }AB || NG, CD || NH.$$ $$∵ ∠NGH = ∠ABH = 30◦, \text{ dan }∠NHG = ∠DCG = 60◦,∠GNH = 180◦ − 30◦ − 60◦ = 90◦.$$ $$∵ BM = CM \Longrightarrow GM = HM,$$ $$∴ GH = 2NM = 6, AD = 7 − 6 = 1.$$ $$∴ EF =\frac{1}{2}(1 + 7) = 4.$$ - Pada trapesium $ABCD, AB || CD, ∠DAB = ∠ADC = 90◦$, dan $\Delta ABC$ berbentuk sama sisi. Diketahui garis tengah trapesium $EF = 0,75a$, tentukan panjang alas bawah $AB$ dalam $a$.
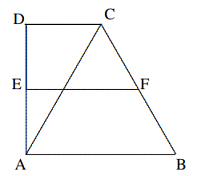
Solusi: Dari kondisi yang diberikan, $$∠DAC = 30◦, ∴ CD =\frac{1}{2}AC =\frac{1}{2}AB.$$ Dengan teorema titik tengah, $$EF=\frac{1}{2}(CD+AB)=\frac{3}{4}AB,$$ $$∴ AB = a.$$ - Pada suatu segiempat cembung $ABCD$, $O$ adalah titik dalam $ABCD$ sehingga $∠AOB = ∠COD = 120◦, AO = OB, CO =OD$. Diketahui $K, L, M$ masing-masing adalah titik tengah segmen $AB, BC, CD$, buktikan bahwa $\Delta KLM$ merupakan segiempat sama sisi.
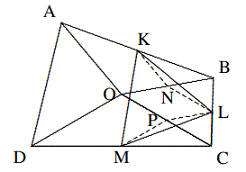
Solusi: Cukup ditunjukkan bahwa $KL = ML$ dan $∠KLM = 60◦$. Kesimpulannya dapat diperoleh dengan teorema titik tengah. Misalkan $N, P$ masing-masing adalah titik tengah $OB, OC$. Hubungkan $NK, NL, PL, PM$. Maka $$KN=\frac{1}{2}OA=\frac{1}{2}OB=PL,$$ $$NL=\frac{1}{2}OC=\frac{1}{2}OD=PM.$$
$$∵ NK || OA, NL || OC, PL || OB, PM || OD \text{ dan},$$ $$∠KNL = ∠AOC = 120◦ + ∠BOC = ∠BOD = ∠LPM,$$ $$∴\Delta KNL \cong \Delta LPM \text{ (S.A.S.)},\text{ maka }KL = LM.$$ Di sisi lain, kita punya $∠KLM = ∠KLN + ∠NLP + ∠PLM = ∠PML + ∠LPC + ∠PLM = 180◦ − ∠CPM = 180◦ − 120◦ = 60◦,$ oleh karena itu $\Delta KLM$ adalah sama sisi. - Diketahui titik $P$ dan $Q$ masing-masing berada pada sisi $AB$ dan $AC$ dari segitiga lancip $ABC$. $D$ adalah titik dalam $\Delta ABC$ sehingga $PD ⊥ AB$ di $P$ dan $QD ⊥ AC$ di $Q$. Jika $M$ adalah titik tengah sisi $BC$, buktikan bahwa $PM = QM$ jika dan hanya jika $∠BDP = ∠CDQ$.
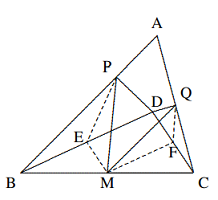
Solusi: Kecukupan: Misalkan $∠BDP = ∠CDQ$. Misalkan $E, F$ masing-masing adalah titik tengah $BD, CD$. Hubungkan $EP, ME, MF, FQ$. Maka $$EP=\frac{1}{2}BD=MF,ME=\frac{1}{2}CD=FQ,$$ $$∵ ∠BDP = ∠CDQ\Longrightarrow ∠PBD = ∠QCD,$$ $$∴ ∠PED = 2∠PBD = 2∠DCQ = ∠DFQ,$$ karena $DEMF$ adalah jajaran genjang, oleh karena itu $$∠DEM = ∠DFM,$$ jadi $∠PEM = ∠MFQ,$ maka $\Delta PEM\cong \Delta MFQ\text{ (S.A.S.)}$, jadi $PM=QM.$
Keharusan: Jika $PM = QM$, maka $\Delta PEM \cong \Delta MFQ \text{ (S.S.S.)}$, jadi $∠PEM = ∠MFQ, ∠DEM = ∠MFD$ (dengan alasan yang sama seperti di atas), oleh karena itu $∠PED = ∠DFQ$, yaitu $2∠PBE = 2∠DCQ$ atau $∠PBE = ∠DCQ$.
Jadi, $∠BDP = 90◦ − ∠PBD = 90◦ − ∠DCQ = ∠CDQ.$
Solusi dari setiap Permasalahan diberikan pada kelas online
“Take the attitude of a student, never be too big to ask questions, never know too much to learn something new.”

