Sisi dan Sudut Segitiga

Pengantar Pemecahan Masalah
Pemecahan masalah atau problem solving adalah proses untuk menemukan solusi dari suatu masalah dengan menggunakan pengetahuan dan keterampilan yang sudah ada. Pemecahan masalah merupakan soft skill yang penting untuk menghadapi tantangan dalam kehidupan sehari – hari, terutama ketika harus menemukan solusi inovatif untuk masalah yang rumit
- Pengetahuan Dasar
- Contoh Soal
Pengetahuan Dasar
- Untuk setiap segitiga, jumlah panjang dua sisinya harus lebih panjang daripada panjang sisi ketiga. Dengan kata lain, selisih panjang dua sisinya harus lebih kecil daripada panjang sisi ketiga.
- Jumlah tiga sudut dalam suatu segitiga adalah $180^o$.
- Jumlah semua sudut dalam poligon bersisi $n$ adalah $(n − 2) × 180^o$.
- Jumlah semua sudut luar poligon bersisi $n$ adalah $360^o$.
- Sudut luar suatu segitiga sama dengan jumlah dua sudut dalam yang berhadapan.
- Untuk sebuah segitiga, sisi yang berhadapan dengan sudut dalam yang lebih besar lebih panjang daripada sisi yang berhadapan dengan sudut dalam yang lebih kecil, dan sebaliknya.
- Untuk segitiga $ABC$ dan $A_1B_1C_1$, jika $AB=A_1B_1,CB=C_1B_1$, maka $AC>A_1C_1$ jika dan hanya jika $\angle ABC > \angle A_1B_1C_1$.
Contoh Soal
- (1) Jika setiap sisi suatu segitiga memiliki panjang yang merupakan faktor prima dari 2001, berapa banyak segitiga berbeda yang ada?
(2) Berapa banyak segitiga sama kaki yang masing-masing sisinya memiliki panjang integral, dan kelilingnya 144?
Solusi:
(1) Karena $2001=3\times 23\times 29$, Segitiga dengan sisi-sisi panjang berikut ada:
{$3,3,3$}; {$23,23,23$}; {$29,29,29$};
{$3,23,23$}; {$3,29,29$}; {$23,29,29$}; {$23,23,29$}.
Total ada 7 kemungkinan segitiga.
(2) Misalkan setiap kaki segitiga sama kaki memiliki panjang $n$, maka alasnya memiliki panjang $144 − 2n = 2(72 − n)$, yaitu panjang alasnya pasti genap.
a) Jika $n\ge 144-2n$, yaitu $3n\ge 144$, maka $n\ge 48$. Karena $2n\le 144-2=142$, yaitu $n\le 71$, kita memiliki $48\le n\le 71$, ada $24$ kemungkinan nilai untuk $n$.
b) Jika $n<144-2n$, maka $n<48$. Dari pertidaksamaan segitiga, $2n>144-2n$, yaitu $n>36$, maka $36<n<48$, jadi $n$ memiliki $47 − 36 = 11$ kemungkinan nilai. - Diberikan sebuah poligon cembung yang jumlah semua sudut dalamnya, kecuali satu, adalah $2200^o$. Temukan sudut dalamnya yang dikecualikan.
Solusi: Karena jumlah sudut dalam poligon cembung bersisi $n$ adalah $(n − 2) \cdot 180^o$, maka $$2200^o=12\times 180^o+40^o=13\times 180^o-140^o$$ maka dapat disimpulkan bahwa $n = 13 + 2 = 15$, dan sudut yang dikecualikan adalah $140^o$. - Seperti yang ditunjukkan pada diagram di bawah ini, pada $\Delta ABC, \angle B > \angle C, AD$ adalah garis bagi dari $\angle BAC, AE ⊥ BC$ di $E$. Buktikan bahwa $\angle DAE =\frac{1}{2}(\angle B − \angle C)$.
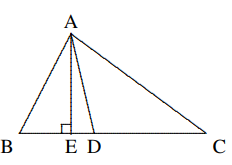
Solusi: Maka
$\angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}(180^o-\angle B – \angle C)$
$=90^o-\frac{1}{2}\angle B-\frac{1}{2}\angle C,$
$\angle DAE=\angle BAD -\angle BAE$
$=\angle BAD-(90^o-\angle B)$
$=90^o-\frac{1}{2}(\angle B+\angle C)-90^o+\angle B$
$=\frac{1}{2}(\angle B-\angle C)$ - Pada gambar di bawah ini, $AB = AC, ∠BAD = 30^o$, dan $AE = AD$. Maka $∠CDE$ sama dengan:
(A) $7.5^o$, (B) $10^o$, (C) $12.5^o$, (D) $15^o$, (E) $20^o$.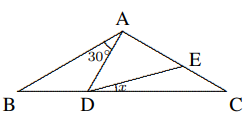
Solusi: Misalkan $\angle CDE=x$, maka
$x=\angle ADC-\angle ADE=\angle ADC-\angle AED$
$=\angle ADC-(x+\angle C),$
$∴x=\frac{1}{2}(\angle ADC-\angle C)$
$=\frac{1}{2}(\angle B+30^o-\angle C)=15^o.$ - Seperti yang ditunjukkan pada gambar, $AB = BC = CD = DE = EF = FG =GH, ∠α = 70^o$. Tentukan besar $∠β$ dalam derajat.
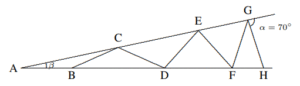
Solusi: $∠A = β ⇒ ∠ACB = β ⇒ ∠CBD = 2β ⇒ ∠CDB = 2β$
$$⇒ ∠ECD = 3β ⇒ ∠CED = 3β ⇒ ∠EDF = 4β ⇒ ∠EF D = 4β$$ $$⇒ ∠GEF = 5β ⇒ ∠EGF = 5β ⇒ ∠GF H = 6β ⇒ ∠GHF = 6β$$ $$⇒ ∠α = 7β.$$ Oleh karena itu $\beta=10^o$. - Seperti yang ditunjukkan pada diagram, $BE$ dan $CF$ masing-masing membagi dua $∠ABD$ dan $∠ACD$. $BE$ dan $CF$ berpotongan di titik $G$. Diketahui $∠BDC = 150◦$ dan $∠BGC = 100◦$, tentukan $∠A$ dalam derajat.
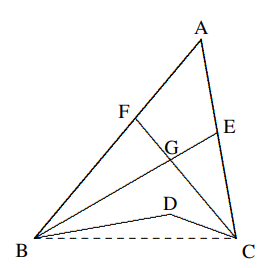
Solusi: Hubungkan $BC$. Kemudian $$∵ ∠BDC + ∠DBC + ∠DCB = 180◦,$$ $$∴ ∠DBC + ∠DCB = 180◦ − 150◦ = 30◦.$$ $$∵ ∠BGC + ∠GBD + ∠GCD + ∠DBC + ∠DCB= 180◦,$$ $$∴ ∠GBD + ∠GCD = ∠BDC − ∠BGC = 50◦.$$
Maka $$∠ABD + ∠ACD = 2 \cdot 50◦ = 100◦,$$ $$∠A = 180◦ − 100◦ − 30◦ = 50◦.$$ - Seperti yang ditunjukkan pada gambar, pada $\Delta ABC$, garis bagi sudut luar $∠A$ dan $∠B$ berpotongan dengan sisi yang berhadapan di $D$ dan $E$ masing-masing, dan $AD = AB = BE$. Maka besar sudut $A$, dalam derajat, adalah
(A) $10^o$, (B) $11^o$, (C) $12^o$, (D) tidak ada yang sebelumnya.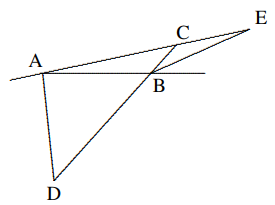
Solusi: Misalkan $∠A = ∠E = α, ∠D =∠ABD= β, ∠CBE = γ, ∠ACB = δ$. Maka $β = 2γ$ dan $ β = α + δ, δ = γ + α, ∴ β = 2α + γ.$ Dari $2γ = β = 2α + γ,$ kita peroleh $γ = 2α,$ juga $β = 4α.$
$$∵\frac{1}{2}(180^o − α) + 2β = 180^o,$$ $$∴ 4β− α = 180◦,$$ $$16α − α = 180◦,$$ $$α= 12◦, ∴ ∠A =12◦.$$ - Terdapat empat titik $A, B, C$, dan $D$ pada bidang tersebut, sehingga setiap tiga titik tidak kolinear. Buktikan bahwa pada segitiga $ABC, ABD, ACD$, dan $BCD$ terdapat setidaknya satu segitiga yang memiliki sudut dalam tidak lebih besar dari $45°$.
Solusi: Cukuplah membahas dua kasus yang ditunjukkan oleh gambar berikut: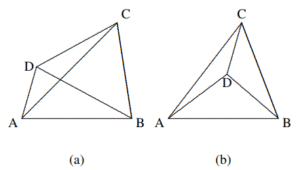
Untuk kasus (a), karena $∠DAB + ∠ABC + ∠BCD + ∠CDA = 360◦$, setidaknya salah satu di antaranya tidak kurang dari $90◦$. Dengan asumsi $∠CDA ≥ 90◦$, maka pada $\Delta CDA,∠DCA + ∠CAD ≤ 90◦$, sehingga salah satu di antaranya tidak lebih besar dari $45◦$.
Untuk kasus (b), karena $∠ADB + ∠ADC + ∠BDC = 360◦$, salah satu dari tiga sudutnya lebih besar dari $90◦$, misalkan $∠ADB > 90◦$, maka $∠DAB + ∠DBA < 90◦$, sehingga salah satu dari $∠DAB$ dan $∠DBA$ kurang dari $45◦$. - Diketahui bahwa dalam segitiga siku-siku, panjang salah satu kaki sudut siku-siku adalah $11$ dan panjang kedua sisi lainnya merupakan bilangan bulat positif. Tentukan keliling segitiga tersebut.
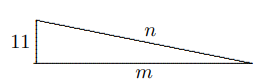
Solusi: Dari kondisi yang diberikan kita memiliki $$n^2=m^2+11^2,$$ $$n^2-m^2=11^2,$$ $$(n-m)(n+m)=121=1\cdot 121=11\cdot 11,$$ oleh karena itu $$n-m=1,n+m=121\text{ atau }n-m=11,n+m=11,$$ $$∴ n = 61, m = 60. (n = 11, m = 0 \text{ tidak tersedia}.)$$
Jadi, kelilingnya adalah $11 + 61 + 60 = 132.$
Solusi dari setiap Permasalahan diberikan pada kelas online
“Do the best you can. No one can do more than that.”

