Beberapa Metode Faktorisasi

- Metode Dasar Faktorisasi
- Contoh Soal
Metode Dasar Faktorisasi
(I) Ekstrak faktor persekutuan dari suku-suku: seperti $$xm+ym+zm=m(x+y+z).$$
(II) Terapkan rumus perkalian: seperti yang disebutkan di Bab 5. Namun, berbeda dengan Bab 5, saat ini setiap rumus diterapkan untuk mengubah ekspresi dalam bentuk non-produk menjadi ekspresi baru dalam bentuk produk.
(III) Perkalian Silang: 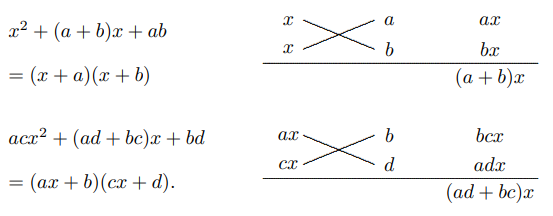
(IV) Dengan mengelompokkan, membagi, atau menyisipkan istilah untuk memperoleh faktor umum.
(V) Dengan mengganti subekspresi untuk menyederhanakan ekspresi yang diberikan.
(VI) Metode penentuan koefisien. Pertama, struktur produk diberikan, kemudian parameter yang tidak diketahui dalam produk ditentukan dengan membandingkan koefisien.
(VII) Faktorisasi polinomial simetris atau siklik.
Contoh Soal
- Faktorkan $(d^2-c^2+a^2-b^2)^2-4(bc-da)^2$.
Solusi: $$(d^2-c^2+a^2-b^2)^2-4(bc-da)^2=(d^2-c^2+a^2-b^2)^2-(2bc-2da)^2$$ $$=(d^2-c^2+a^2-b^2-2bc+2da)(d^2-c^2+a^2-b^2+2bc-2da)$$ $$=[(d+a)^2-(b+c)^2]\cdot [(d-a)^2-(b-c)^2]$$ $$=(d+a-b-c)(d+a+b+c)(d+b-a-c)(d+c-a-b).$$ - Faktorkan $64x^6-729y^12$.
Solusi: $$64x^6-729y^12=(2x)^6-(3y^2)^6=[(2x)^3-(3y^2)^3][(2x)^3+(3y^2)^3]$$ $$=(2x-3y^2)[(2x)^2+(2x)(3y^2)+(3y^2)^2]\cdot (2x+3y^2)[(2x)^2-(2x)(3y^2)+(3y^2)^2]$$ $$=(2x-3y^2)(2x+3y^2)(4x^2+6xy^2+9y^4)(4x^2-6xy^2+9y^4).$$ - Faktorkan masing-masing ekspresi berikut:
(i) $2x^2+x-6;$
(ii) $2x^2-10x+8.$
Solusi: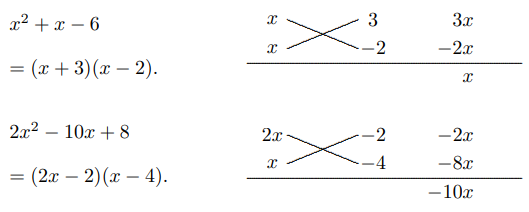
- Faktorkan $2a^3+6a^2+6a+18.$
Solusi: $$2a^3+6a^2+6a+18=2[(a^3+3a^2+3a+1)+8]=2[(a+1)^3+2^3]$$ $$=2(a+3)[(a+1)^2-2(a+1)+4]=2(a+3)(a^2+3)$$ - Faktorkan (i) $x^4+2x^3+7x^2+6x-7;$ (ii) $x^3+9x^2+23x+15$
Solusi: Misalkan $y=x^2+x$. Maka
(i) $x^4+2x^3+7x^2+6x-7=x^2(x^2+x)+x(x^2+x)+6(x^2+x)-7$
$=(x^2+x+6)(x^2+x)-7=y^2+6y-7=(y+7)(y-1)$
$=(x^2+x+7)(x^2+x-1)$
(ii) $x^3+9x^2+23x+15=x^2(x+1)+8x(x+1)+15(x+1)$
$=(x+1)(x^2+8x+15)=(x+1)(x+3)(x+5).$ - Faktorkan (i) $(a+1)(a+2)(a+3)(a+4)-120;$ (ii) $x^5+x+1$.
Solusi:
(i) $(a+1)(a+2)(a+3)(a+4)-120$
$=[(a+1)(a+4)][(a+2)+(a+3)]-120$
$=(a^2+5a+4)(a^2+5a+6)-120$
$=[(a^2+5a+5)-1][(a^2+5a+5)+1]-120$
$=(a^2+5a+5)^2-121=(a^2+5a+5)^2-11^2$
$=(a^2+5a-6)(a^2+5a+16)=(a-1)(a+6)(a^2+5a+16).$
(ii) $x^5+x+1=(x^5-x^2)+(x^2+x+1)$
$=x^2(x^3-1)+(x^2+x+1)$
$=x^2(x-1)(x^2+x+1)+(x^2+x+1)$
$=(x^2+x+1)[x^2(x-1)+1]=(x^2+x+1)(x^3-x^2+1).$ - Faktorkan $(2y-3z)^3+(3z-4x)^3+(4x-2y)^3.$
Solusi: Misalkan $2y-3z=a,3z-4x=b,4x-2y=c$, maka $a+b+c=0$.
Karena $$(2y-3z)^3+(3z-4x)^3+(4x-2y)^3=a^3+b^3+c^3$$ $$=(a^3+b^3+c^3-3abc)+3abc$$ $$=(a+b+c)(a^2+b^2+c^2-bc-ca-ab)+3abc$$ $$=3abc=3(2y-3z)(3z-4x)(4x-2y).$$ - Faktorkan $(3a+3b-18ab)(3a+3b-2)+(1-9ab)^2$
Solusi: Ekspresi yang diberikan simetris di $3a$ dan $3b$, jadi kita menggunakan $u=3a+3b,v=(3a)(3b)$ untuk menyederhanakan ekspresi. Kemudian $$(3a+3b-18ab)(3a+3b-2)+(1-9ab)^2=(u-2v)(u-2)+(1-v)^2$$ $$=u^2-2uv-2u+4v+v^2-2v+1=(u^2-2uv+v^2)+2(v-u)+1$$ $$=(v-u)^2+2(v-u)+1=(v-u+1)^2$$ $$=(9ab-3a-3b+1)^2=[(3a-1)(3b-1)]^2=(3a-1)^2(3b-1)^2.$$ Catatan: Jangan berhenti di $(v-u+1)^2$ - Faktorkan $2x^2+7xy-4y^2-3x+6y-2$.
Solusi: Jika diketahui $2x^2+7xy-4y^2=(2x-y)(x+4y)$, maka $$2x^2+7xy-4y^2-3x+6y-2=(2x-y+a)(x+4y+b)$$ Dengan mengeluarkan hasil perkalian tersebut, diperoleh bahwa $$(2x-y+a)(x+4y+b)=2x^2+7xy-4y^2+(a+2b)x+(4a-b)y+ab$$ Dengan membandingkan koefisien, diperoleh sistem persamaan berikut $$a+2b=-3\text{ }\text{ }\text{ }\text{ }\text{ }(6.1)$$ $$4a-b=6,\text{ }\text{ }\text{ }\text{ }\text{ }(6.2)$$ $$ab=-2.\text{ }\text{ }\text{ }\text{ }\text{ }(6.3)$$ Maka $2\times (6.2)+(6.1)$ menghasilkan $9a=9$, yaitu $a=1$. Dari $(6.2),b=6-4a=-2$. Karena $(a,b)=(1,-2)$ memenuhi $(6.3)$, dan ini adalah solusi unik, kami memperoleh $$2x^2+7xy-4y^2-3x+6y-2=(2x-y+1)(x+4y-2).$$ - Diketahui $x^5-5qx+4r$ memiliki faktor $(x-c)^2$ untuk suatu konstanta $c$. Buktikan bahwa $q^5=r^4$.
Solusi: Jika $c=0$, maka $x^2|x^5-5qx+4r\Rightarrow r=q=0$, Kesimpulannya adalah benar. Ketika $c\neq 0$, kondisinya berarti $$x^5-5qx+4r=(x^2-2cx+c^2)(x^3+ax^2+bx+d)$$ $$x^5+(a-2c)x^4+(c^2+b-2ac)x^3+(ac^2-2bc+d)x^2+(bc^2-2cd)x+c^2d..$$ Kemudian perbandingan koefisien menghasilkan persamaan berikut: $$a=2c,\text{ }b=2ac-c^2=3c^2,\text{ }d=2bc-ac^2=4c^3=\frac{4r}{c^2}\Rightarrow r=c^5.$$ Lebih jelas, $$5q=2cd-bc^2=8c^4-3c^4=5c^4\Rightarrow q=c^4$$ Jadi, $$q^5=c^{20}=r^4.$$
Solusi dari setiap Permasalahan diberikan pada kelas online
“The pessimist sees difficulty in every opportunity. The optimist sees opportunity in every difficulty. ”

