- Untuk setiap bilangan bulat positif $n$ (ditulis tanpa angka nol di depan), misalkan $t(n)$ sama dengan bilangan yang dibentuk dengan membalik digit $n$. Misalnya, $t(461) = 164$ dan $t(560) = 65$. Untuk berapa banyak bilangan bulat positif tiga digit $m$ yang $m + t(t(m))$ ganjil?
- Robert memiliki dua tumpukan kartu berisi lima kartu bernomor 1–5, yang satu dikocok secara acak sementara yang lainnya diurutkan berdasarkan angka. Ia memilih salah satu tumpukan secara acak dan membalik tiga kartu pertama, masing-masing bernomor 1, 2, dan 3. Berapa probabilitas kartu berikutnya bernomor 4?
- Milo melempar lima dadu yang sama rata, masing-masing memiliki 4, 6, 8, 12, dan 20 sisi (dan masing-masing diberi label 1-n untuk n yang sesuai). Berapa banyak cara berbeda mereka dapat melempar dadu full house (tiga angka satu dan dua angka lainnya)? Angka yang sama yang muncul pada dadu yang berbeda dianggap sebagai full house yang berbeda, sehingga (1, 1, 1, 2, 2) dan (2, 2, 1, 1, 1) keduanya akan dihitung.
- Ada 5 orang di sebuah pesta. Untuk setiap pasangan, ada peluang 1/2 mereka berteman, terlepas dari pasangan lainnya. Tentukan banyaknya pasangan orang yang memiliki teman bersama, tetapi mereka sendiri bukan teman.
- Pada tabel di bawah ini, tempatkan angka 1–12 pada sel yang diarsir. Anda mulai dari sel tengah (ditandai dengan ∗). Anda
berulang kali bergerak ke atas, ke bawah, ke kiri, atau ke kanan, dipilih secara acak setiap kali, hingga mencapai sel yang diarsir. Skor Anda adalah angka pada sel yang diarsir yang Anda dapatkan.
Misalkan $m$ adalah nilai harapan terkecil dari skor Anda (berdasarkan cara Anda menempatkan angka-angka tersebut), dan $M$ adalah nilai harapan terbesar dari skor Anda. Hitung $m \cdot M$.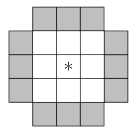
- Michael dan James sedang bermain lempar dart secara bergantian di papan dart sederhana. Setiap lemparan dart bernilai 25 poin atau 50 poin. Mereka mencatat urutan skor per lemparan (yang dibagi di antara mereka), dan pada lemparan pertama, jika tiga skor terakhir berjumlah 125, pemain yang melempar dart terakhir menang. Pada setiap lemparan, setiap pemain memiliki peluang 2/3 untuk mendapatkan skor yang mereka inginkan, dan peluang 1/3 untuk mendapatkan skor lainnya. Misalkan Michael melempar lebih dulu, dan dua lemparan pertama keduanya bernilai 5. Jika kedua pemain menggunakan strategi optimal, berapa probabilitas Michael menang?
- Jika $S = \{s_1, s_2, . . . , s_n\}$ adalah himpunan bilangan bulat dengan $s_1 < s_2 < · · · < s_n$, definisikan $$f(S)=\sum_{k=1}^{n}(-1)^kk^2s_k.$$ (Jika $S$ kosong, $f(S) = 0$.) Hitung nilai rata-rata $f(S)$ ketika $S$ berkisar pada semua subset dari $\{1^2, 2^2, . . . , 100^2\}$.
- Enam pembunuh bayaran, bernomor 1-6, berdiri membentuk lingkaran. Setiap pembunuh bayaran secara acak diberi target sehingga setiap pembunuh bayaran memiliki target yang berbeda dan tidak ada pembunuh bayaran yang menjadi targetnya sendiri. Dalam urutan angka yang meningkat, setiap pembunuh bayaran, jika mereka masih hidup, membunuh target mereka. Tentukan jumlah pembunuh bayaran yang masih hidup pada akhir proses ini.
- Misalkan $S$ menyatakan $\{1, . . . , 100\}$, dan misalkan $f$ merupakan permutasi dari $S$ sehingga untuk semua $x ∈ S, f(x) \neq x$. Untuk semua $f$ tersebut, tentukan jumlah maksimum elemen $j$ yang memenuhi $$\underset{j\text{ kali}}{\underbrace{f(…(f(j))…)}}=j$$
- Misalkan 100 orang berkumpul di sebuah taman, masing-masing membawa sebuah amplop berisi nama mereka (semua nama mereka berbeda). Kemudian, amplop-amplop tersebut dipindah-pindahkan secara seragam dan acak di antara orang-orang tersebut. Jika $N$ adalah jumlah orang yang mendapatkan amplop aslinya, carilah nilai harapan dari $N^5$.
Keranjang Belanja
