- Perhatikan diagram jalan yang menghubungkan enam tempat di bawah ini.
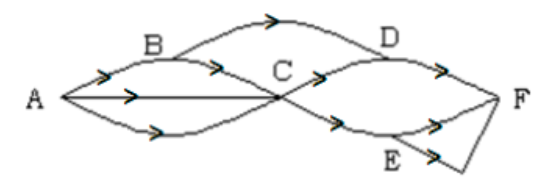 Banyaknya cara menuju tempat F dari tempat A, dengan syarat arah pergerakan dari kiri ke kanan (sebagai contoh dari C tidak boleh kembali ke B), adalah . . . .
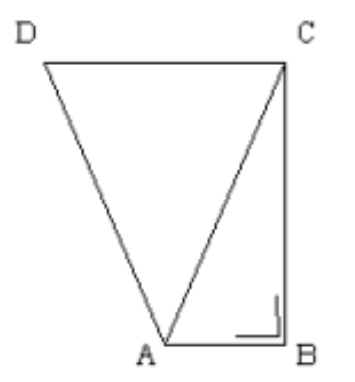
Banyaknya cara menuju tempat F dari tempat A, dengan syarat arah pergerakan dari kiri ke kanan (sebagai contoh dari C tidak boleh kembali ke B), adalah . . . . - Pada gambar berikut, ABC adalah segitiga siku-siku di B, sedangkan ACD adalah suatu segitiga sama kaki (AC = AD) dengan luas 20 satuan luas. Luas trapesium ABCD adalah . . . satuan luas.
- If A is the smallest positive integer divisible by 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, then A = . . .
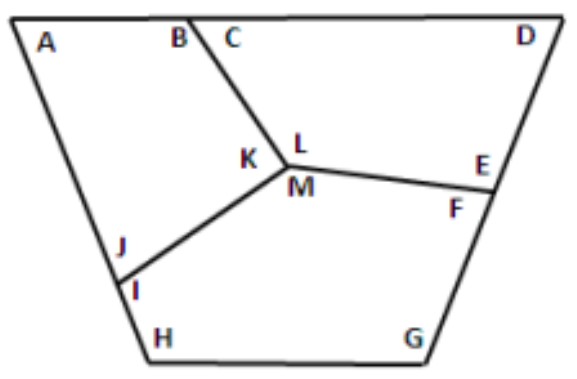
- The shape in the figure below has 13 interior angles. The sum of all interior angles is . . . $\circ$.
- Pak Amat memiliki suatu neraca dan tiga buah anak timbangan yang terdiri atas anak timbangan dengan berat 1 kg, 3 kg, dan 9 kg. Dengan alat tersebut, Pak Amat dapat menimbang benda A yang beratnya 2 kg dengan cara berikut.
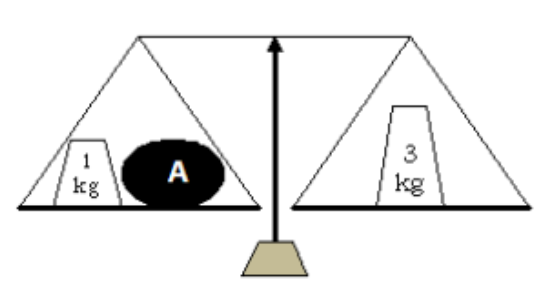 Berat benda paling ringan (dalam bentuk bilangan bulat) yang tidak dapat ditimbang Pak Amat adalah . . . kg.
Berat benda paling ringan (dalam bentuk bilangan bulat) yang tidak dapat ditimbang Pak Amat adalah . . . kg. - Rata rata dari empat bilangan bulat yang berbeda adalah 50. Jika bilangan yang terkecil adalah 45, maka bilangan terbesar yang mungkin dari keempat bilangan tersebut adalah . . .
- If A + B + C = 210, A = 4B and A = 14C, then the value of A is . . .
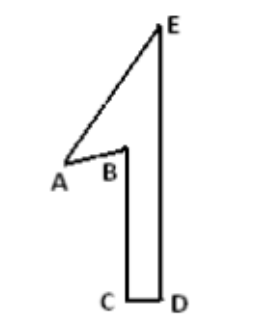
- Perhatikan gambar seperti angka satu berikut ini. Besar sudut AED adalah $35\circ$, dan besar sudut BAE adalah $40\circ$. Besar sudut BCD sama dengan sudut CDE yaitu $90\circ$. Besar sudut ABC adalah . . . $\circ$.
- Firly mengikuti suatu lomba lari jarak 24 km. Karena persiapan fisiknya yang kurang, dia dapat menyelesaikan dengan cara berlari selama 10 menit, kemudian berjalan selama lima menit, berlari lagi selama 10 menit, berjalan lagi selama lima menit, dan demikian seterusnya. Dia tiba di garis akhir lomba ketika dia menyelesaikan 10 menit lari ke lima kalinya. Jika kecepatannya berlari dua kali kecepatan berjalan, maka kecepatan Firly berlari adalah . . . m/menit.
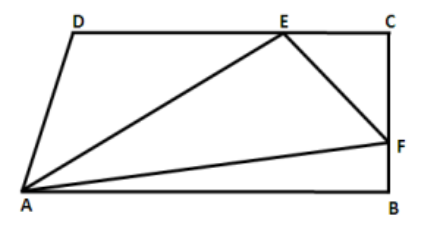
- Diketahui trapesium ABCD dengan AB sejajar CD. Pada trapesium tersebut dibentuk segitiga APB dengan P terletak pada sisi CD. Jika ukuran sisi AB sama dengan tiga kali ukuran sisi CD, perbandingan luas segitiga APB dan trapesium ABCD adalah . . . :
- Jumlah 25 bilangan asli berbeda sama dengan 2013. Jika $x$ adalah bilangan terkecil di antara 25 bilangan tersebut, maka nilai x terbesar yang mungkin adalah . . .
- In the figure below, ABCD is a trapezium and $\angle ABC = 90\circ$. $\overline{AB}$ = 20 cm, $\overline{BC}$ = 8 cm, and $\overline{CD}$ = 16 cm. Point E lies on CD and point F lies on BC. $\overline{EC} = \overline{CF}$ = 6 cm. The area of triangle AFE is . . . $cm^2$.
- Ali dan Budi akan menyelesaikan sebanyak 10 tugas P dan 12 tugas Q. Ali dapat menyelesaikan satu tugas P dalam waktu 3 menit dan satu tugas Q dalam 5 menit. Budi dapat menyelesaikan satu tugas P dalam waktu 6 menit dan satu tugas Q dalam 4 menit. Mereka mulai mengerjakan tugas-tugas tersebut secara bersama-sama pukul 07.00 dan tidak beristirahat sampai semua tugas tersebut selesai. Paling cepat, mereka dapat menyelesaikan semua tugas tersebut pada pukul . . .
- Amir, Budi, dan Candra mula-mula berdiri pada posisi segaris dari timur ke barat, Budi di antara Amir dan Candra. Ketiganya menghadap ke utara. Jarak Amir ke Budi adalah 2 meter, sedangkan Budi dan Candra berjarak 3 meter. Apabila Candra berjalan maju sejauh 5 meter dan Amir tetap berdiri di tempatnya, maka agar posisi ketiganya tetap segaris Budi harus maju sejauh . . . m.
- Tiga bilangan prima berbeda dikalikan menghasilkan suatu bilangan baru. Banyaknya semua faktor berbeda dari bilangan baru tersebut adalah . . .
- Ukuran alas akuarium 60 cm × 30 cm dan tingginya 50 cm. Akuarium diisi air $\frac{2}{3}$ bagian. Sebuah balok yang tingginya 1 m tetapi luas alasnya belum diketahui, dimasukkan ke dalam akuarium. Saat alas balok tersebut menyentuh alas akuarium setengah dari air yang ada di akuarium telah tumpah keluar. Luas alas balok tersebut adalah . . . $cm^2$.
- Bilangan tiga digit ABC mempunyai sifat :a. A + B + C = 18b. B − C = 1c. CBA − ABC = 396Bilangan ABC tersebut adalah . . .
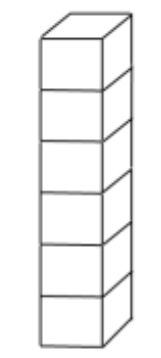
- Pada setiap dadu, jumlah noktah pada muka-muka yang berlawanan selalu sama dengan tujuh. Enam buah dadu ditumpuk seperti pada gambar di bawah ini. Pada tumpukan itu jumlah noktah pada dua muka yang bersentuhan sama dengan enam. Banyaknya noktah pada muka atas dari dadu paling atas adalah . . . buah.
- The first digit of the smallest number, which the sum of its digits is 2013, is . . .
- Banyaknya persegi panjang berbeda ukuran yang mempunyai panjang sisi berupa bilangan bulat dan luasnya 2013 satuan luas adalah . . . buah.
- Pada jam digital, waktu 23 : 57 adalah salah satu contoh waktu yang semua angka digitnya menunjukkan bilangan-bilangan prima berbeda (2, 3, 5, 7). Dalam sehari semalam, jam digital tersebut menunjukkan waktu yang semua angka digitnya menunjukkan bilangan-bilangan prima berbeda sebanyak . . . kali.
- Latif mempunyai sebatang logam dengan panjang 2 m yang akan dibuat menjadi beberapa gelang dalam dua ukuran berdiameter 7, 7 cm atau 8, 4 cm. Sisa batang logam terpendek yang mungkin didapat Latif setelah pembuatan gelang-gelang tersebut adalah . . . cm. ($\pi =\frac{22}{7}$)
- Banyak bilangan tiga angka yang apabila dibagi 12 atau dibagi 13 mempunyai sisa yang sama adalah . . . buah.
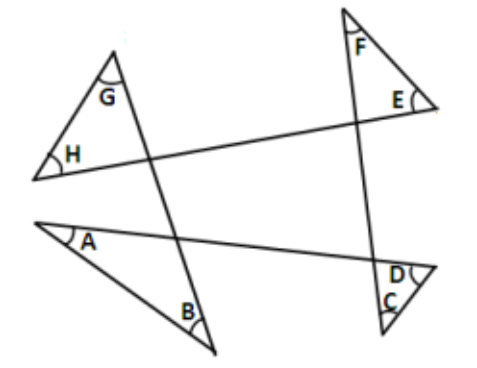
- $\angle A + \angle B + \angle C + \angle D + \angle E + \angle F + \angle G = . . . \circ$.
- Suatu toko menjual empat jenis cokelat. Ali, Budi, Candra, Didi, dan Endang masing-masing membeli dua batang cokelat yang berbeda di toko tersebut dan membayar berturut-turut Rp 13.000, Rp 15.000, Rp 19.000, Rp 20.000, dan Rp 22.000. Total harga keempat jenis cokelat tersebut adalah Rp. . . .
SOAL URAIAN
- Karena macet, pada 10 km pertama dari jarak 20 km yang harus dilaluinya, Amir terpaksa mengendarai sepeda motornya dengan kecepatan 25 km/jam. Berapakah kecepatan rata-rata Amir 10 km berikutnya agar kecepatan rata-ratanya pada jarak 20 km tersebut 40 km/jam?
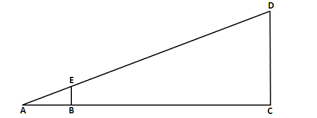
- In the figure below, BC = 10 cm, CD = 8 cm, and BE = 2 cm. EB and DC are perpendicular to AC. What is the length of AB?
- Dana untuk perbaikan tiga kantor pemerintah (kelurahan, kecamatan, dan kabupaten) di suatu kabupaten berjumlah Rp. 350 juta. Dana untuk perbaikan kantor kelurahan adalah setengah dari dana untuk perbaikan kantor kecamatan, dan dana untuk perbaikan kantor kabupaten sebanyak dua kali dari dana untuk perbaikan kantor kecamatan. Berapa banyak dana untuk perbaikan kantor kecamatan?
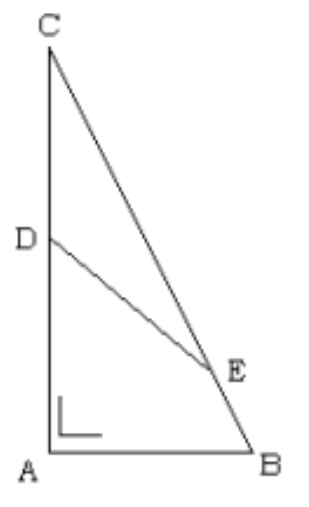
- Pada gambar berikut segitiga ABC siku-siku di A dan CD = DE. Jika diketahui sudut ADE = $70\circ$, berapakah besar sudut ABE?
- What is the smallest value of positive integer A so that 7560 × A is a square number?
- Sebuah tabung berjari-jari 25 cm dan tinggi 50 cm berisi penuh dengan air. Air tersebut sebagian dituangkan ke dalam tabung lain yang kosong yang berjari-jari 40 cm dan tinggi 30 cm sampai tinggi air pada kedua tabung sama. Berapakah tinggi air pada kedua tabung?
- Pak Maman, Pak Asep, dan Pak Ujang memasang ubin bersama-sama, dengan kecepatan memasang ubin yang berbeda-beda. Jika Pak Maman memasang empat buah ubin, Pak Asep hanya dapat memasang tiga buah ubin. Jika Pak Maman memasang enam buah ubin, Pak Ujang dapat memasang tujuh buah ubin. Banyaknya ubin yang dipasang ketiganya adalah 420 buah. Tentukan banyaknya ubin yang dipasang Pak Ujang.
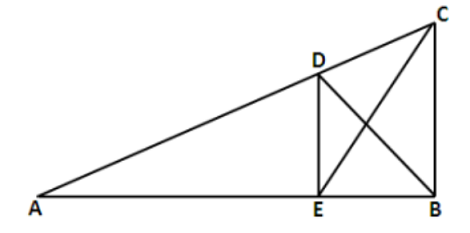
- Pada gambar di bawah, segitiga ABC siku-siku di B dan DE sejajar CB. Jika AE : BE = 2 : 1 dan luas $\Delta ABD$ = 8, berapakah luas $\Delta CDE$?
- Pembangunan suatu gedung harus diselesaikan dalam waktu 100 hari dan dapat diselesaikan dalam waktu tersebut oleh 30 orang. Setelah dikerjakan selama 20 hari, ternyata pekerjaan tersebut berhenti selama 20 hari karena banjir. Agar pembangunan gedung tersebut dapat diselesaikan tepat waktu, berapa banyak perkerja yang harus ditambah?
- Kita akan membagi seperempat lingkaran dengan jari-jari 4 cm menjadi lima buah bagian A, B, C, D, dan E, dengan masing-masing luas
yang sama besar. Caranya adalah dengan membuat dua seperempat lingkaran dengan jari-jari r dan R dengan pusat yang sama dengan seperempat lingkaran asal, lalu membagi dua dua juring terluar seperti diperlihatkan gambar di bawah. Berapakah nilai $R^2$?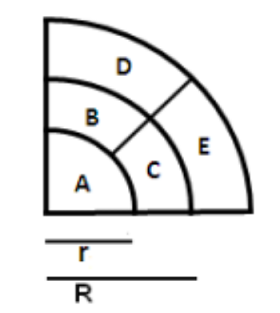
- Pada pukul 00.00 tanggal 1 Januari 2013, seseorang mengeset tiga buah jam. Pukul 00.00 keesokan harinya, ternyata dia mendapati jam pertama menunjukkan waktu yang tepat, jam yang kedua terlambat enam menit, dan jam yang ketiga kelebihan sepuluh menit. Jika ketiga jam tersebut terus dijalankan dan memiliki kecepatan berputar yang tetap, tanggal berapakah ketiga jam tersebut menunjukkan waktu yang sama lagi untuk pertama kalinya?
- The area of triangle ABC = 9$cm^2$.
ADEF is a rectangle, and AD = 2 CD.
What is the area of BFDE?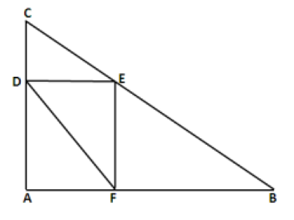
- Andi memberitahu Budi bahwa hasil kali tiga bilangan bulat positif A, B, dan C adalah 36.
Andi juga memberitahu Budi berapa jumlah tiga bilangan tersebut. Ternyata Budi tetap tidak tahu persis berapa saja bilangan-bilangan tersebut. Berapakah jumlah ketiga bilangan tersebut?
SOAL EKSPLORASI
- Ganti setiap huruf A, B, C, D, E, dan F dengan angka antara 0 dan 9. Huruf yang sama melambangkan angka yang sama sedangkan huruf yang berbeda juga melambangkan angka yang berbeda. Hasil penggantian harus memenuhi tiga syarat yaitu :a. Bilangan ABC dan Bilangan CBD masing-masing bilangan prima.b. Bilangan BBC dan Bilangan CDF masing-masing bilangan kuadrat.c. Bilangan ACE dan Bilangan ECF masing-masing bilangan berpangkat tiga.
- The following table shows the answers of five students namely A, B, C, D, and E to six true(T)-or-false(F) questions:
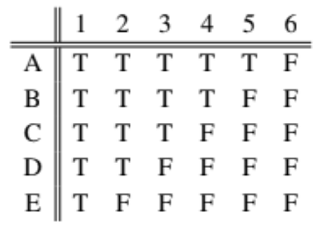 From the table above we see that student A answers true for question 1, true for question 2, true for question 3, true for question 4, true for question 5, and false for question 6. If the total number of incorrect answers of all five students answers is 9, what is the correct answer for each question?
From the table above we see that student A answers true for question 1, true for question 2, true for question 3, true for question 4, true for question 5, and false for question 6. If the total number of incorrect answers of all five students answers is 9, what is the correct answer for each question? - Seorang dermawan berniat menyumbangkan uang sebesar Rp. 2.000.000.000 untuk sejumlah perpustakaan sekolah. Dia ingin menyumbangkan seluruh uang tersebut kepada tepat 100 sekolah. Dia ingin menyumbang Rp. 60.000.000 untuk tiap SMA, Rp. 40.000.000 untuk tiap SMP, dan Rp. 10.000.000 untuk tiap SD. Sebagai contoh dia dapat menyumbangkannya pada 20 SMA dan 80 SD.Tentukan semua kemungkinan komposisi banyaknya SMA, SMP, dan SD yang memungkinkan keinginan dermawan tersebut dapat terlaksana.
